The multiplication rule for independent events helps quantify how likely two events are to occur together, emphasizing how independence shapes probability relationships in random processes.

Understanding the Multiplication Rule

The multiplication rule for independent events is a foundational tool used to determine the likelihood that two events occur simultaneously. When events are independent, the occurrence of one event does not influence or alter the likelihood of the other. This rule provides a direct way to evaluate combined outcomes in random processes and supports the broader framework of probability reasoning required in AP Statistics.

Introducing Independent Events in Context

Two events are considered independent when knowledge of one event’s outcome does not change the probability of the other event occurring. This notion of independence is essential because the multiplication rule relies on the assumption that the two probabilities remain unaffected by each other.

Understanding this relationship ensures that the multiplication rule is used appropriately and only when the independence condition is satisfied. When events are not independent, a different approach to probability is required, involving conditional probability rather than direct multiplication.

The Multiplication Rule Explained

The multiplication rule describes how to calculate the probability that both event A and event B occur together, also referred to as their joint probability. The rule states that the chance of both events happening equals the probability of the first event multiplied by the conditional probability of the second event occurring after the first.

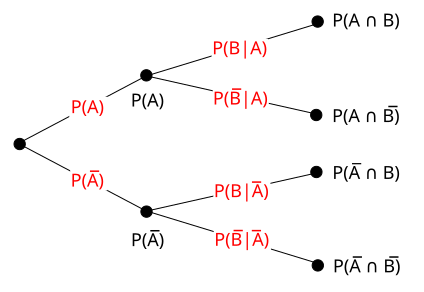
Probability tree diagram for two events A and B. Each branch is labeled with either a marginal probability such as P(A) or a conditional probability such as P(B|A), and each endpoint shows the corresponding joint probability (for example, P(A ∩ B)). The additional branches involving complements Ā and B̄ extend beyond the AP focus but help illustrate how the multiplication rule applies to all possible joint outcomes. Source.

EQUATION

When events are independent, the conditional probability of B given A simplifies because knowing A has occurred provides no new information about B. This simplification leads to a special form of the multiplication rule used specifically for independent events.

A brief reminder that independence must be established before applying this simplified form helps ensure accuracy in probability evaluation and prevents misapplication of the rule where conditional dependence exists.

The Special Case for Independent Events

For independent events, the multiplication rule becomes much simpler. Because the probability of event B is not influenced by event A, the conditional probability $\text{P(B|A)}$ equals $\text{P(B)}$. This allows the formula to reduce to a direct product of the two individual probabilities, reflecting the complete lack of influence between the events.

EQUATION

This formulation is central to AP Statistics because it provides a mathematically sound and efficient method for determining the likelihood of combined independent outcomes. It preserves the structural characteristics of independence and ensures that probability calculations reflect the nature of the random process being studied.

A clear recognition of when to use this form of the multiplication rule strengthens a student’s ability to analyze probability scenarios effectively, particularly in situations involving repeated or unrelated random events.

Applying the Multiplication Rule Conceptually

While AP Statistics does not require examples within this section, understanding how and when the multiplication rule applies conceptually is crucial for problem-solving across the course. The rule is often used in the context of repeated independent trials, simultaneous random events, or any situation where two outcomes must occur together without influencing one another.

Key Points for Identifying Independence

Students should focus on recognizing independence through contextual reasoning and information provided in probability settings. The following considerations help determine whether the multiplication rule for independent events is appropriate:

• Check whether the problem states or implies independence. Independence is often explicitly given or can be inferred from the situation.

• Confirm that one event does not alter the likelihood of the other. This requires interpreting descriptions of random processes carefully.

• Distinguish independence from mutually exclusive events. Mutually exclusive events cannot occur together, whereas independent events can occur together without influencing each other.

• Evaluate whether repeated trials share identical conditions. Consistent probabilities across trials indicate independence in many scenarios.

Importance in Statistical Reasoning

Understanding the multiplication rule for independent events supports deeper engagement with probability models and strengthens the ability to construct and interpret complex probability statements. This rule also serves as a precursor to more advanced topics, such as probability distributions, expected values, and applications of randomness in statistical inference.

By mastering the multiplication rule, students gain a reliable tool for quantifying joint likelihoods in independent settings and for supporting conclusions drawn from structured probability reasoning.

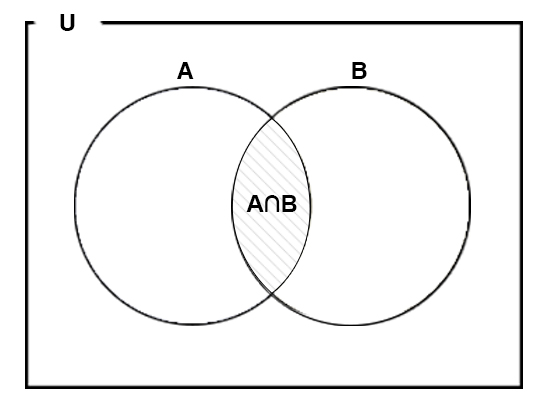
Venn diagram illustrating the intersection of events A and B within a universal set U. The shaded region represents A ∩ B, the outcomes belonging to both events simultaneously. The inclusion of explicit set labels goes slightly beyond the immediate syllabus requirement but remains entirely consistent with AP Statistics notation. Source.