Understanding Independent Events

Independent events form a foundational idea in probability, emphasizing situations where knowing that one event occurred provides no information about whether another event will occur. This concept supports accurate probability calculations in many statistical contexts.

What Independence Means in Probability

When studying random processes, patterns often emerge, and it becomes essential to determine whether these patterns reflect meaningful relationships or simply chance. One key relationship explored in probability is independence, which tells us whether two events influence one another. Independence helps determine when the probability of one event should remain unchanged, even when another event is known to have happened.

In probability contexts, independence is not assumed automatically; it must be established based on information about the scenario or through known probability structures. Once independence is confirmed, it becomes a powerful simplifying tool for calculating probabilities involving multiple events.

Characterizing Independent Events

Independence centers on the stability of probabilities under additional information. If event A and event B are independent, the likelihood of B remains identical whether or not A occurs. This relationship is reciprocal: the probability of A also remains unchanged by the occurrence of B. Understanding this symmetry is essential because it emphasizes that independence is a mutual property, not a one-directional claim.

A useful way to conceptualize independence is to contrast it with dependence. When events are dependent, the outcome of one provides meaningful information about the outcome of the other. For independent events, no such information is gained. The probability structure of one event remains fully intact, regardless of knowledge about the other.

Independent events often arise in repeated trials of the same random process, such as multiple tosses of a fair coin or rolls of a fair die.

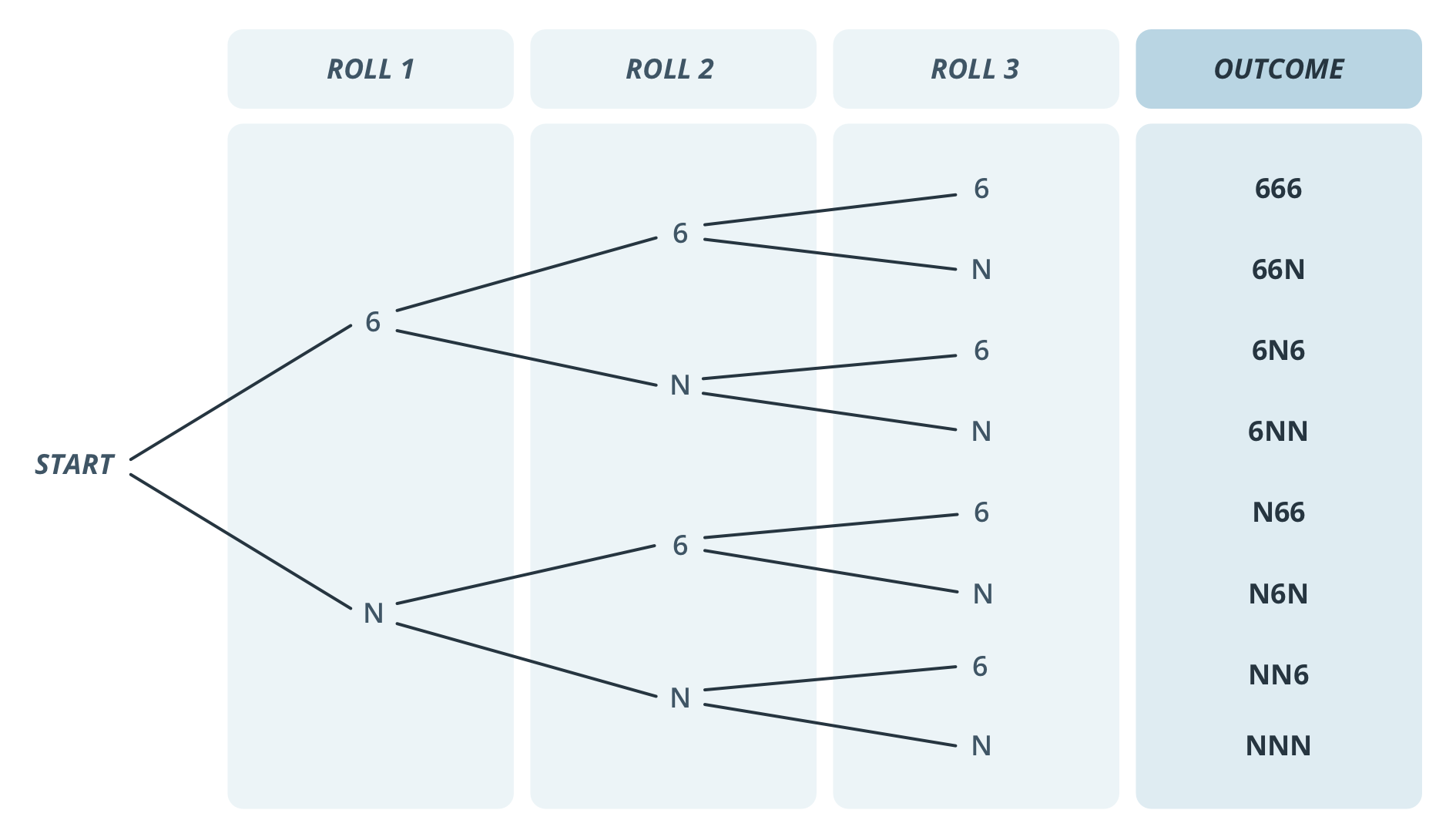
Tree diagram for three independent die rolls, with branching that repeats the same structure at each stage because each roll is independent. Each complete path represents a possible sequence such as 6NN. This visual highlights how independent events combine through repeated, unaffected probability stages. Source.

Mathematical Expression of Independence

While the meaning of independence can be stated verbally, probability theory formalizes the idea. AP Statistics students should understand how independence is represented mathematically because this expression is foundational for later applications involving joint probabilities.

EQUATION

This equation expresses that, for independent events, the probability of both events occurring together equals the product of their individual probabilities. This relationship works only when events are independent; if the product does not equal the joint probability, the events are not independent. Because of its importance, this condition becomes a standard test for independence in statistical analysis.

The equation also reinforces the conceptual definition: if learning that A occurred changes the expected frequency of B, then multiplying their individual probabilities will not correctly represent the joint probability. Therefore, independence must be confirmed before using this condition in calculations.

Recognizing When Events Are Independent

Students must be able to recognize independence conceptually and mathematically. Identifying independence typically involves one of the following:

• Determining that the context explicitly states independence.

• Evaluating whether knowing one event affects the likelihood of the other.

• Using probability values to verify the independence condition.

• Understanding the underlying random mechanism to decide whether outcomes influence each other.

Contextual reasoning plays an important role. Two events may appear unrelated, but unless it is known that the outcome of one does not alter the probability of the other, independence should not be assumed. AP Statistics emphasizes careful justification rather than intuitive guesses.

The event ‘A and B’ (the intersection) consists of outcomes that belong to both A and B at the same time.

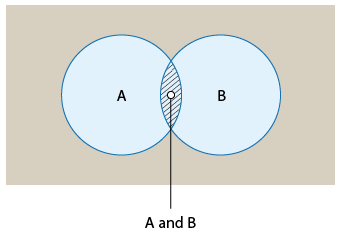
Venn diagram illustrating events A and B with their overlapping region representing A ∩ B. This figure clarifies the geometric meaning of the intersection used when evaluating independence. While it does not itself indicate independence, it displays the region whose probability is compared with $P(A)P(B)$. Source.

Why Independence Matters

Independence is central to the structure of probability because it allows simplification of otherwise complex calculations. Many statistical methods rely on the assumption of independent events or independent random variables. When independence holds, combining probabilities becomes more straightforward, supporting clearer interpretation of outcomes and stronger statistical conclusions.

Independence also forms the basis for later probability rules, including those involving the multiplication of probabilities for independent events. Without establishing independence, these rules cannot be used reliably. Thus, developing a strong understanding of independent events is fundamental for progressing into more advanced statistical reasoning.

Indicators of Independence in Real-World Contexts

Although AP Statistics avoids relying solely on intuition, real-world situations often provide clues about independence. These situations may involve:

• Physical processes where one outcome cannot influence another

• Random mechanisms specifically designed to maintain independence

• Scenarios where trials are repeated under identical conditions

These clues help develop informed expectations about independence, but probability verification remains necessary when data or outcomes must be analyzed mathematically.

Summary of Key Features of Independent Events

To consolidate an operational understanding of independence, students should remember the following essential points:

• Independence means no influence between the outcomes of events.

• Probabilities remain unchanged when independence is present.

• Mathematical confirmation relies on verifying the independence condition.

• Independence must be justified, not assumed, unless explicitly stated in the scenario.

Through these principles, independent events become a fundamental tool for reasoning accurately about probability in a wide range of statistical applications.