In this subsubtopic, you learn how to turn the numerical results of a significance test into a clear yes-or-no decision about population differences using p-values.

Making decisions in a significance test for two proportions

After computing a test statistic and its p-value for a difference of population proportions, you must decide what that result implies for the null hypothesis H0: p1 - p2 = 0. The AP syllabus emphasizes making this decision by comparing the p-value to a preselected significance level α.

The role of the significance level α

Before looking at the data, researchers choose a significance level, often α = 0.05, that sets the threshold for how unlikely the sample result must be, assuming the null hypothesis is true, in order to count as convincing evidence against H0.

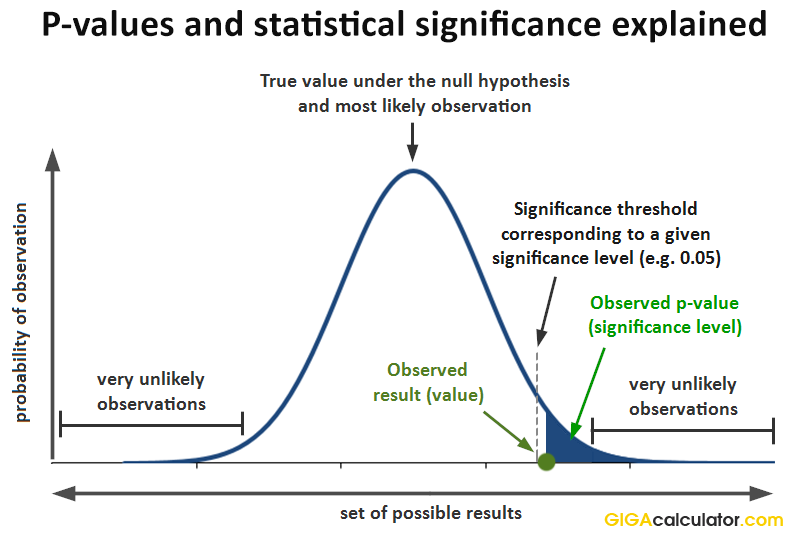
This diagram shows the relationship between the observed test statistic, the p-value tail region, and the significance threshold α. It visually reinforces how α acts as a cutoff for determining statistical significance. The numeric values in the plot are example-specific, but the conceptual structure applies to tests of population proportions. Source.

Once α is chosen, it should not be changed after seeing the p-value.

Key ideas about α:

• α is chosen in advance, typically 0.10, 0.05, or 0.01, depending on how cautious the researcher wants to be.

• Smaller α means stronger evidence is required to reject H0, leading to fewer rejections but more conservative decisions.

• Larger α means weaker evidence is enough to reject H0, increasing the chance of rejecting H0 when it is actually true.

Understanding the p-value for decision making

The p-value summarizes how compatible the sample data are with the null hypothesis. For this subsubtopic, you do not need to compute the p-value; you only need to interpret it for decision making once it has been calculated correctly, taking into account whether the test is one-sided or two-sided.

Important features of the p-value:

• A small p-value means the observed difference in sample proportions (or a more extreme one) would rarely occur if H0: p1 - p2 = 0 were true.

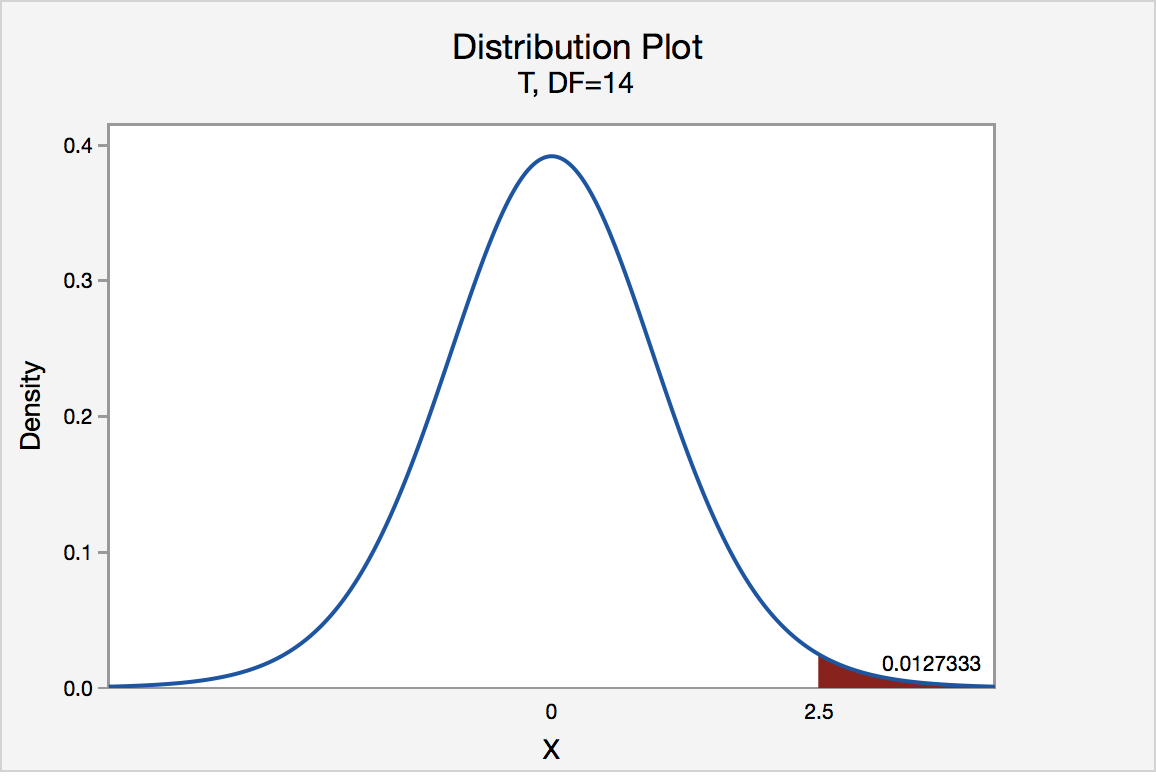
This figure displays a sampling distribution with the p-value represented as a shaded tail area. Although shown with a t-distribution, the same idea applies to the z-distribution used for two-proportion tests: the p-value measures how likely it is to see a result as extreme as the observed one if the null hypothesis is true. Source.

• A large p-value means the observed difference is reasonably likely under H0 and therefore not surprising enough to count as strong evidence against H0.

• The interpretation always assumes that all conditions for inference have been met and that the test statistic is valid.

The formal decision rule

The AP syllabus statement for this subsubtopic defines a clear rule:

• If the p-value ≤ α, reject the null hypothesis H0: p1 - p2 = 0.

• If the p-value > α, do not reject the null hypothesis.

This rule directly connects the numerical p-value to a yes-or-no decision, using the preselected α as the cutoff between “sufficient” and “insufficient” evidence against H0.

Interpreting “reject” and “do not reject”

When you apply the decision rule, the language you use is very important.

• Reject H0: The data provide sufficient statistical evidence to conclude that there is a significant difference between the two population proportions in the direction described by the alternative hypothesis Ha.

• Do not reject H0: The data do not provide sufficient statistical evidence for a difference in population proportions in the direction described by Ha.

Notice that “do not reject H0” is not the same as “accept H0.” Failing to reject means the evidence is not strong enough to support Ha, not that H0 has been proven true. There may still be a real difference; the sample just does not reveal it clearly at the chosen significance level.

Step-by-step decision process

Once you know the p-value and α, making a decision follows a consistent sequence:

• State the null hypothesis H0: p1 - p2 = 0 and the alternative hypothesis Ha with its inequality sign (<, >, or ≠).

• Identify the significance level α that was chosen before seeing the data.

• Compare the p-value from the test to α.

• Use the formal rule:

  • If p-value ≤ α, reject H0.

  • If p-value > α, do not reject H0.

• Express the decision in context, explaining what it says about the difference between the two population proportions.

Linking decisions to evidence about population proportions

The final part of the syllabus description emphasizes that this decision step determines whether the data provide enough evidence to suggest a significant difference between the two population proportions. Your conclusion should connect the statistical decision back to the real-world question about the populations being compared, making it clear whether the evidence supports a claim of a difference or leaves that claim unconfirmed at the chosen significance level.