A confidence interval offers structured evidence about a population mean, allowing researchers to evaluate whether a statistical claim is plausible by comparing claimed values to the interval’s supported range.

Understanding How Confidence Intervals Support Claims

When a confidence interval is used to assess a claim about a population mean, it provides a range of plausible values for that mean based on sample data. Claims are evaluated by determining whether the claimed value is consistent with this interval or if the data suggest that the claim is inconsistent with the plausible values implied by the sample.

A claim in statistical inference is a statement asserting something about a population parameter.

Confidence intervals help justify claims because they incorporate sampling variability and quantifiable uncertainty. If the claimed value does not fall within the interval, the interval indicates that the sample data are not compatible with that claim.

Interpreting Consistency and Inconsistency with a Claim

A confidence interval’s relationship to a claimed value forms the central justification:

• If the claimed mean falls within the confidence interval, the data are considered consistent with the claim.

• If the claimed mean falls outside the confidence interval, the data provide evidence that the claim is not supported, given the observed variability.

These evaluations hinge on understanding that a confidence interval does not guarantee the true population mean’s location but instead expresses plausible values based on the sample and chosen confidence level.

Using Context to Support or Refute Claims

Because statistical inference depends on random sampling, any justification must be connected explicitly to the research question and the data collection process. A value outside the interval suggests that if the study were repeated under similar conditions, it is unlikely the sample would yield results consistent with the claim. Therefore, justification statements must reflect both the statistical conclusion and the contextual meaning for the population studied.

The Role of Confidence Level When Justifying Claims

Confidence intervals vary in width based on their confidence level, affecting how claims are assessed:

• Higher confidence levels produce wider intervals, making it more likely that a claimed value lies within the interval.

• Lower confidence levels create narrower intervals, offering more precision but increasing the chance of excluding the claimed value.

Thus, the justification for accepting or rejecting a claim depends on the confidence level that guided construction of the interval. This connection underscores why students should state the confidence level clearly when interpreting an interval’s relationship to a claim.

A confidence interval also reflects the variability of sample data, which is why repeated sampling would generate intervals that sometimes capture the true mean and sometimes do not.

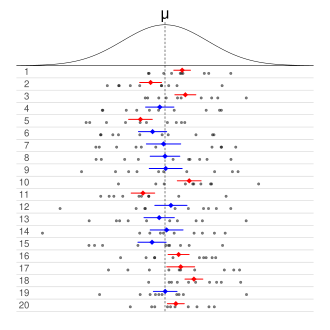
This figure shows many confidence intervals constructed from repeated random samples. Intervals that include the true mean μ differ in color from those that miss it, illustrating long-run confidence behavior and the role of sampling variability. Source.

How the Interval Structure Guides Claim Evaluation

Confidence intervals incorporate both the sample mean and the margin of error, forming the range of plausible values.

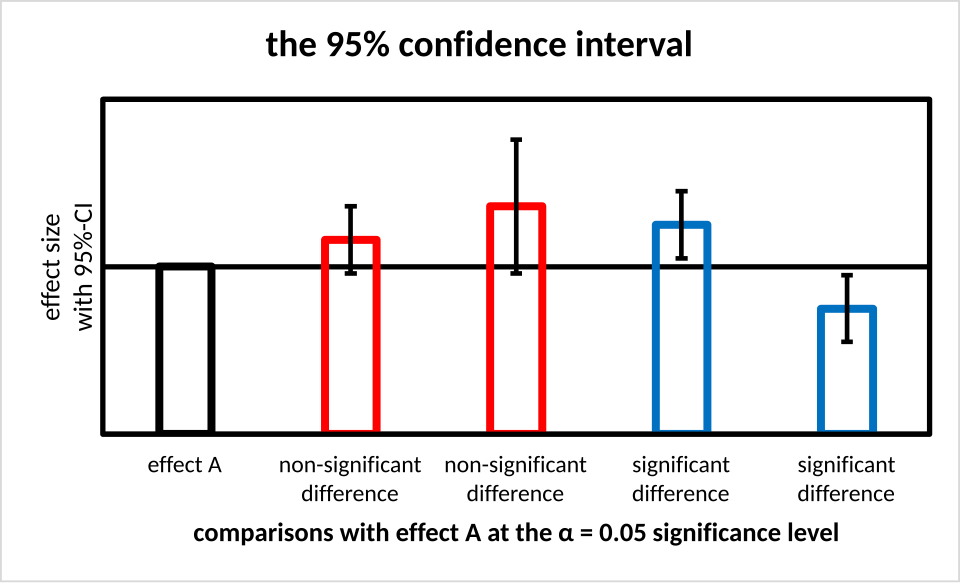
This bar chart displays sample means with 95% confidence intervals as vertical error bars. Any hypothesized mean falling outside an interval is inconsistent with that sample’s evidence. The presence of multiple groups exceeds the syllabus scope, but the interpretation of each individual interval is fully aligned with AP Statistics. Source.

EQUATION

Although the computation itself is not the focus of this subsubtopic, understanding this structure helps explain why a claim may or may not be supported. A claim’s relationship to the interval depends on the combined influence of sample variability and chosen confidence level.

Confidence intervals do not offer proof; instead, they provide evidence. If the claim lies outside the interval, the data suggest that such a parameter value is unlikely given the sample. However, if the claim lies inside the interval, the evidence does not contradict the claim—even though it does not prove it true.

Communicating Justification Clearly

When explaining whether a claim is justified using a confidence interval, students should:

• Restate the claim in context.

• Specify whether the claimed value is inside or outside the interval.

• Use the language of consistency rather than certainty.

• Connect the conclusion explicitly to the population of interest.

• Emphasize that the justification depends on sampling variability and the confidence level.

Checklist for Justifying a Claim with a Confidence Interval

• Identify the claim and the population parameter involved.

• State the confidence interval clearly and in context.

• Compare the claim to the interval:

  • Inside → claim is consistent with the data.

  • Outside → data do not support the claim.

• Discuss uncertainty, noting that the interval is one of many possible intervals that could arise from repeated sampling.

• Explain the decision in the context of the statistical question and the population.

Confidence intervals thus serve as a foundational tool for evaluating claims about population means by balancing evidence, uncertainty, and contextual understanding.