AP Syllabus focus:
‘Recognize the inverse relationship between sample size and the width of the confidence interval: as sample size increases, the interval's width decreases.
- Understand that the interval width is directly proportional to the margin of error and inversely proportional to the square root of the sample size.
- Acknowledge that higher confidence levels lead to wider intervals, as they aim to increase the likelihood of containing the true mean.’
Confidence interval width depends on several interconnected factors. Understanding how sample size, margin of error, and confidence level influence interval behavior strengthens accurate interpretation of statistical estimates for population means.
Confidence Interval Width and Its Determinants
Confidence intervals express the plausible range of values for a population mean, and their width reflects the precision of the estimate. AP Statistics emphasizes the relationships among sample size, margin of error, and confidence level, each of which shapes how narrow or wide an interval becomes.
The Role of the Margin of Error
The margin of error describes how far sample-based estimates may vary from the true population mean due to random sampling. A wider margin of error produces a wider confidence interval, reducing precision. Its behavior links directly to sample variability and confidence level, making it essential to understand how the margin of error responds to changes in sample size and critical values.
EQUATION
= Critical value associated with the chosen confidence level
= Sample standard deviation
= Sample size
Because the margin of error is multiplied directly in the confidence interval formula, any factor that increases ME also increases the confidence interval width. The margin of error therefore functions as the mechanism through which confidence level and sample size influence precision.
Inverse Relationship: Sample Size and Interval Width
A central syllabus requirement is recognizing the inverse relationship between sample size and confidence interval width. As sample size increases, the standard error decreases, which shrinks the margin of error and narrows the interval. Larger samples produce more stable estimates of the population mean, reducing the uncertainty expressed by the interval.
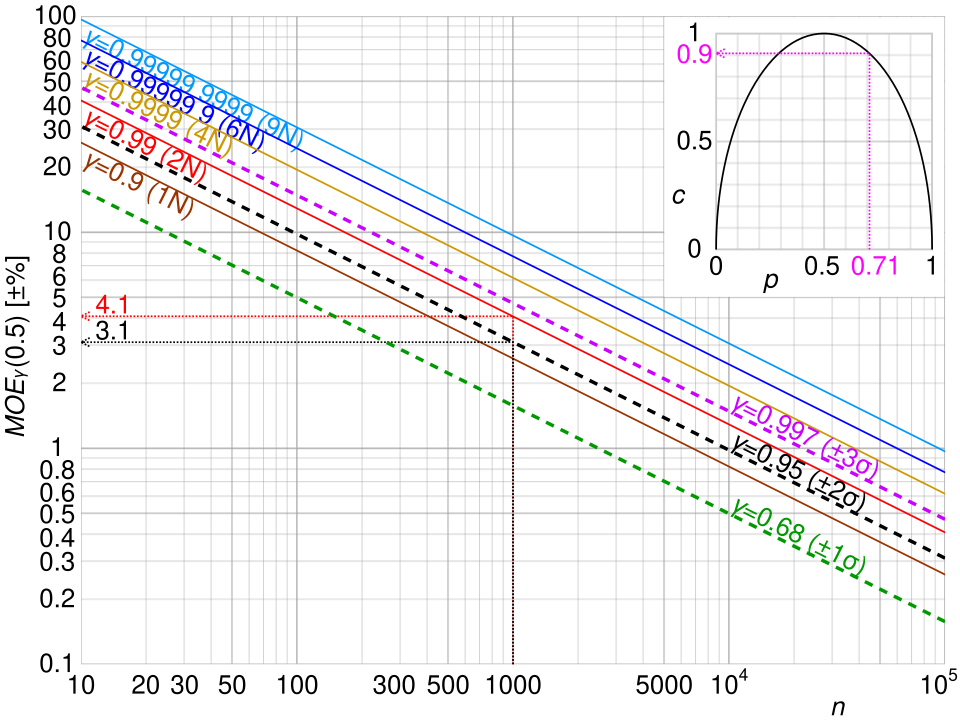
This figure shows how the margin of error decreases as sample size increases and increases as confidence level rises, illustrating the relationships that determine confidence interval width. Source.
Standard Error of the Mean: The estimated standard deviation of the sampling distribution of the sample mean, calculated as .
Because standard error depends on the square root of sample size, doubling n does not halve the interval width; instead, the reduction occurs at a diminishing rate. This inverse-square-root relationship explains why extremely large samples are sometimes needed to achieve small improvements in precision.
A narrower interval resulting from a larger sample size should not be interpreted as increased confidence but rather increased precision. Confidence refers to the long-run success rate of the interval procedure, whereas width reflects how much uncertainty remains.
Direct Relationship: Margin of Error and Interval Width
Interval width is directly proportional to the margin of error. Any increase in margin of error—whether caused by higher variability, smaller sample size, or a larger critical value—expands the interval. This direct proportionality is a structural feature of confidence intervals for means, as the interval is constructed by adding and subtracting the margin of error from the sample mean.
When interpreting the width, students should consider what factors contributed to the margin of error’s magnitude and how those factors reflect the quality of the underlying data and sampling framework.
Influence of the Confidence Level
Higher confidence levels lead to wider confidence intervals. Increasing the confidence level increases the critical value t*, which directly multiplies the standard error. This reflects the trade-off between confidence and precision: to be more confident that the interval captures the true mean, we must broaden the interval to allow for more potential values.
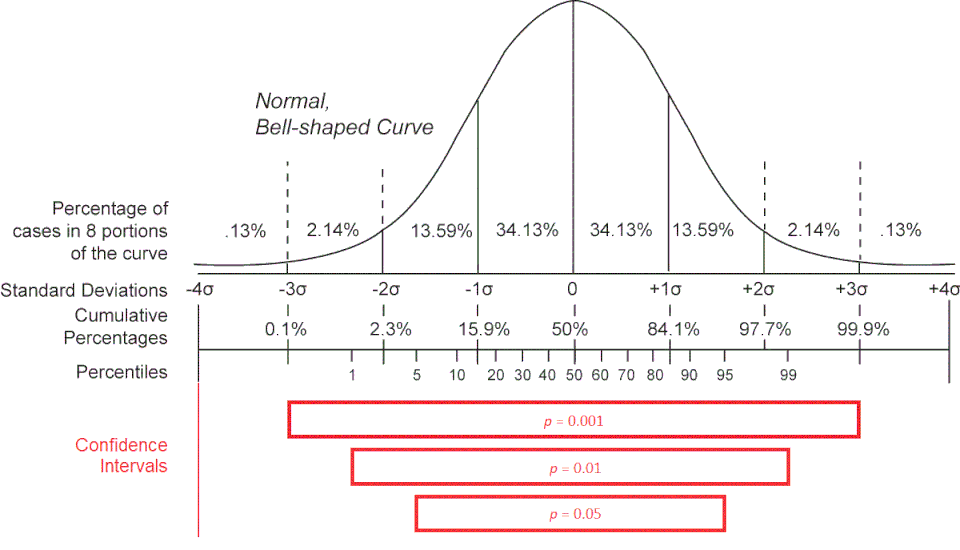
This image displays intervals of varying widths under a normal distribution, demonstrating how higher confidence levels require wider intervals to ensure greater long-run capture rates. Source.
Critical Value: A multiplier obtained from the t-distribution that determines how far sample means must deviate from the population mean to achieve a given confidence level.
Higher confidence levels such as 99% therefore include more area in the distribution tails and produce larger critical values, which increase the width of the confidence interval.
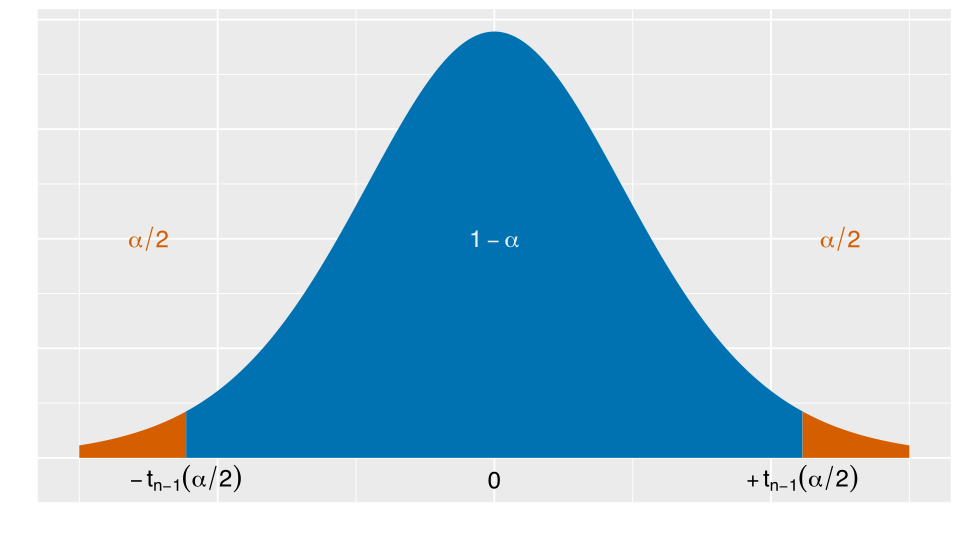
This diagram illustrates how confidence level corresponds to the middle probability mass of the t-distribution and how tail areas define the critical values that determine interval width. Source.
Understanding the Interconnected Relationships
The syllabus emphasizes an integrated understanding of how sample size, margin of error, and confidence level interact. These relationships can be summarized conceptually:
Increasing sample size → decreases standard error → decreases margin of error → narrows interval.
Increasing confidence level → increases critical value t* → increases margin of error → widens interval.
Increasing variability in the sample (larger s) → increases standard error → increases margin of error → widens interval.
These relationships help students assess the reliability and precision of confidence intervals in practical contexts. By understanding the mathematical and conceptual foundations behind interval width, students become better equipped to evaluate whether a confidence interval provides sufficient information to address meaningful questions about a population mean.
FAQ
The standard error of a sample mean decreases with the square root of the sample size. This means each additional observation contributes progressively less reduction in variability.
As a result, doubling the sample size does not halve the interval width; instead, width shrinks more slowly as sample size grows large.
This explains why very large samples are often required to achieve noticeably narrower intervals.
Population variability influences the sample standard deviation, which feeds directly into the margin of error. Higher variability weakens the narrowing effect of increasing sample size.
In highly variable populations, very large samples may be required to tighten intervals meaningfully.
Lower variability strengthens the effect, allowing smaller samples to produce reasonably precise intervals.
Critical values rise more sharply as confidence levels approach the extremes (such as near 99%). This is because more area must be captured in the centre of the distribution, pushing the cut-off points further into the tails.
As a result, a shift from 95% to 99% confidence can widen an interval far more than a shift from 90% to 95%.
No. Increasing sample size improves precision by narrowing the interval but does not change the confidence level, which is set by the researcher.
Confidence describes the long-run performance of the method, while precision describes how narrow the resulting interval is for a given study.
Larger sample sizes therefore enhance the usefulness of the estimate without altering how often the method succeeds in repeated sampling.
Researchers often compare the width of the interval with the scale of the measurement or with thresholds relevant to the research question.
Useful considerations include:
• Whether the interval spans values that would lead to different practical decisions
• Whether the width is small relative to typical variation in the population
• Whether collecting more data is feasible to narrow the interval further
This evaluation is context-dependent but grounded in understanding how width reflects uncertainty.
Practice Questions
Question 1 (1–3 marks)
A researcher constructs a 95% confidence interval for a population mean using a sample of size 40. They then construct a second 95% interval using a sample of size 160 from the same population.
a) State whether the second interval will be wider, narrower, or the same width as the first.
b) Explain why this occurs in terms of sampling variability.
Question 1
a) 1 mark: Correctly states that the second interval will be narrower.
b) 1–2 marks: Explains that increasing sample size reduces standard error, which reduces the margin of error, leading to a narrower confidence interval. Must mention decreased sampling variability.
Question 2 (4–6 marks)
A study investigates the average time students spend revising each week. A 90% confidence interval for the population mean is calculated using a moderate sample size. The researcher considers changing to a 99% confidence level while keeping the same sample data.
a) State how the width of the new confidence interval will compare to the original.
b) Explain how changes in the critical value and margin of error influence this change in width.
c) Describe how the relationships between sample size, confidence level, and interval width help researchers plan reliable studies.
Question 2
a) 1 mark: States that the new interval at 99% confidence will be wider.
b) 2–3 marks: Explains that a higher confidence level requires a larger critical value, which increases the margin of error. Must connect increased margin of error to increased interval width.
c) 1–2 marks: Describes that larger sample sizes narrow intervals, higher confidence levels widen them, and these relationships help determine required sample sizes for desired precision. Answers should reference the trade-off between confidence and precision.

