Confidence intervals for a regression slope allow statisticians to assess whether sample evidence supports or contradicts claims about population relationships, using interval bounds to evaluate plausible values for the true slope.

Understanding Claims in the Context of Regression Slopes

A confidence interval for the slope represents a range of plausible values for the population slope β, based on sample data. This range reflects sampling variability and helps determine whether the data provide evidence supporting or refuting a claim about the linear relationship between two quantitative variables.

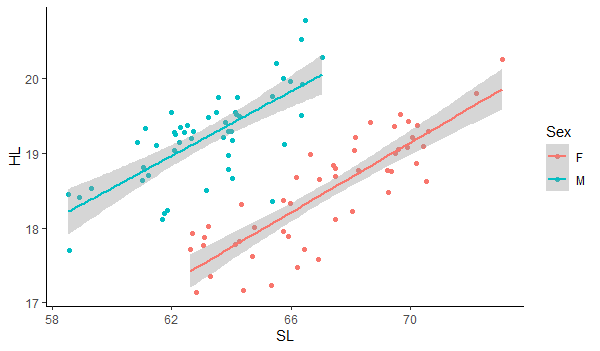
Scatter plot of head length versus standard length for fish, with separate regression lines and shaded confidence intervals for each sex. The shaded bands show the range of plausible lines supported by the sample data, illustrating uncertainty in the estimated slopes. The presence of two groups is extra detail beyond the syllabus, but reinforces how confidence intervals help justify claims about relationships in different populations. Source.

How Confidence Intervals Support or Refute Claims

A claim about a population slope asserts something about the strength or direction of the relationship between variables. A confidence interval allows us to test whether that claim is consistent with plausible values of β. If the claimed value lies inside the interval, the claim is considered plausible; if it lies outside, the claim is not supported by the sample evidence.

Interpreting Interval Bounds in Context

Because interval bounds indicate the range of slopes compatible with the data at a chosen confidence level, the meaning of the interval directly informs the evaluation of claims.

• If zero is not in the interval, the data support the presence of a linear relationship.

• If zero is included, the data do not rule out the possibility of no linear relationship.

• If a specific claimed slope value falls outside the interval, evidence contradicts that claim.

• If the claimed value lies within the interval, the claim remains consistent with the sample data.

These interpretations rely on the foundational idea that in repeated sampling, about C% of constructed intervals will capture the true population slope.

Key Terminology for Justifying Claims

After introducing a definition, continue with clear explanation to reinforce conceptual understanding. In this case, noting how confidence intervals reflect uncertainty helps students appreciate why claims must be assessed relative to the entire interval rather than a single estimate.

Why Confidence Intervals Allow Claim Evaluation

Confidence intervals incorporate both the point estimate (the sample slope b) and the standard error, which captures variability across hypothetical repeated samples.

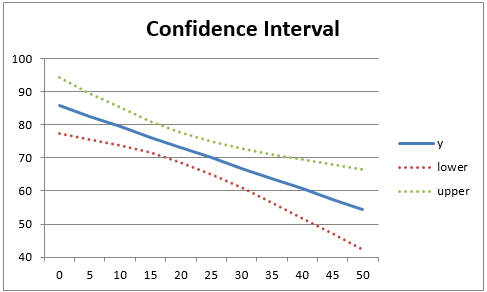
Regression confidence interval chart showing a fitted line with dotted curves above and below representing a 95% confidence band for the mean response. The band illustrates how the combination of the sample slope and its standard error yields a range of plausible regression lines, which can be used to support or refute claims about the underlying relationship. The chart also shows variation in uncertainty across predictor values, a nuance beyond the core AP syllabus. Source.

These elements ensure that the interval represents not just the best estimate of β but also the uncertainty associated with sampling.

Evaluating claims through this interval approach aligns with statistical reasoning: decisions are made based on whether the data’s estimated range of plausible slopes aligns with the stated claim about the population.

Using Confidence Intervals in Statistical Arguments

When justifying a claim, students should rely on clear, context-driven statistical arguments. Strong justifications reference all three components:

• The claim about β

• The confidence interval bounds

• The relationship between the claim and the interval

Essential Points for Justifying Claims

• A claim is supported when its proposed value of β falls within the interval.

• A claim is not supported when its proposed value lies outside the interval.

• Claims about the existence of a relationship depend on whether zero is included.

• Claims about the direction of a relationship depend on the sign of all values in the interval.

• Any justification should reference the population represented by the sample.

A normal explanatory sentence must follow any equation box when included, ensuring clarity and flow.

Evaluating the Strength of Evidence

Confidence intervals also convey how strong the evidence is:

• Narrow intervals provide more precise information about β, strengthening argumentation.

• Wide intervals indicate greater uncertainty, requiring more cautious claims.

• If the interval narrowly excludes or includes a value, evidence may be borderline.

• Large gaps between the claim and interval bounds indicate strong contradiction.

This aligns with the syllabus emphasis on using interval bounds to evaluate hypotheses and claims regarding relationships between variables.

Communicating Justifications Effectively

Students should structure their justification using quantitative and contextual reasoning:

• State the interval clearly.

• Refer explicitly to the claim value.

• Compare the claim to the interval bounds.

• Describe what the interval implies about the population slope.

• Connect the argument to the study context.

This approach mirrors the reasoning used in formal inference while reinforcing the connection between sample data and population conclusions.