A significance test for a regression slope relies on understanding the p-value, which indicates how compatible the sample’s observed slope is with the null hypothesis.

Interpreting the p-Value for a Regression Slope

Understanding the Role of the p-Value

When performing a significance test for the slope of a regression model, the p-value quantifies the strength of evidence against the null hypothesis (H₀), which typically states that the population slope β equals some hypothesized value, often zero. Because regression slope inference centers on determining whether a linear relationship exists between two quantitative variables, interpreting the p-value correctly is essential for drawing accurate conclusions.

Definition of the p-Value

The first time the term appears, it requires clarification.

This probability statement reflects how surprising the sample’s results would be if the null hypothesis accurately described the population relationship.

A p-value is always computed under the assumption that H₀ is true, and therefore it does not measure the probability that the null hypothesis is correct. Rather, it evaluates how consistent the observed sample slope is with a world in which the hypothesized slope is exactly valid.

Connecting the p-Value to the Regression Slope

Interpreting a p-value in the context of regression focuses on the slope estimate, denoted b, and how far this estimate deviates from the hypothesized slope β₀. If the observed slope differs substantially from β₀ relative to its standard error, the resulting test statistic will be large in magnitude, producing a small p-value.

EQUATION

This equation highlights how slope variability is incorporated into the significance test. A more extreme t-value corresponds to stronger evidence against the null hypothesis and therefore a smaller p-value.

Because regression inference assumes conditions such as linearity, independence, normality of residuals, and constant variability, the meaningfulness of the p-value depends on these conditions being sufficiently met. If assumptions fail, the calculated p-value may no longer represent the intended probability.

What a p-Value Tells Us

A correctly interpreted p-value addresses a precise probability statement:

• It gives the likelihood of observing the sample slope or something more extreme, in repeated samples of the same size, if the true population slope equals the hypothesized value.

• It does not give the probability that the null hypothesis is true or false.

• It does not describe the magnitude or practical significance of the relationship between variables.

A small p-value (typically ≤ α, such as 0.05) indicates that the sample data would be unlikely if the null hypothesis were true, providing evidence for a nonzero slope in the population. Conversely, a large p-value suggests insufficient evidence to conclude that the slope differs from the hypothesized value. The comparison between the p-value and the significance level α formalizes this idea.

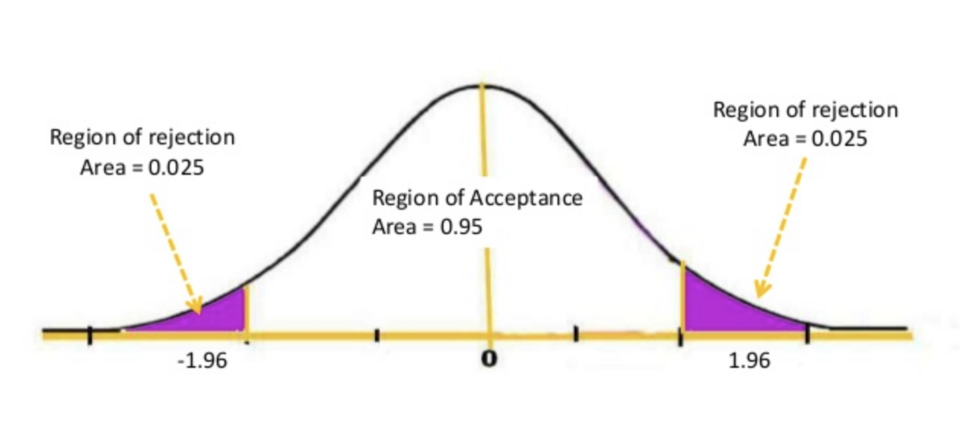
This figure shows a bell-shaped distribution with a central acceptance region and shaded tail regions representing rejection areas. Under the null hypothesis, the test statistic is expected to fall in the central region most frequently, while values in the shaded tails are unusually extreme. The tails visually correspond to very small p-values, which indicate evidence against the null hypothesis and motivate rejecting it when they are at most α; the diagram includes some extra labeling beyond the AP syllabus but reinforces the same concept. Source.

Using the p-Value to Make Inferences

To understand the strength of evidence provided by the p-value, consider how varying magnitudes influence interpretation:

• Very small p-value (e.g., < 0.01): Strong statistical evidence that the true slope differs from β₀.

• Moderate p-value (e.g., around 0.05): Some evidence against the null hypothesis, though conclusions may depend on context and chosen significance level.

• Large p-value (e.g., > 0.10): Little evidence against the null; the observed slope is reasonably plausible under the hypothesized value.

These interpretations align with the AP Statistics emphasis on describing results in context, noting both the sample from which the slope is estimated and the population to which conclusions apply.

Interpreting the p-Value in Context

When interpreting a p-value for a regression slope, students should incorporate these elements:

• Identify the slope being tested and specify the null hypothesis.

• State the p-value as a probability under the assumption that the null hypothesis is true.

• Clarify whether the observed relationship provides convincing evidence of a nonzero population slope.

• Connect the conclusion explicitly to the variables under study.

For example, statements should reference the relationship between the explanatory and response variables and the population parameters they represent. A context-based interpretation highlights that the p-value quantifies uncertainty in the slope estimate rather than certainty about real-world effects.

In the context of regression, a significance test for the slope asks whether the observed relationship between x and y in the sample is strong enough, relative to random variation, to conclude that there is a genuine linear association in the population.

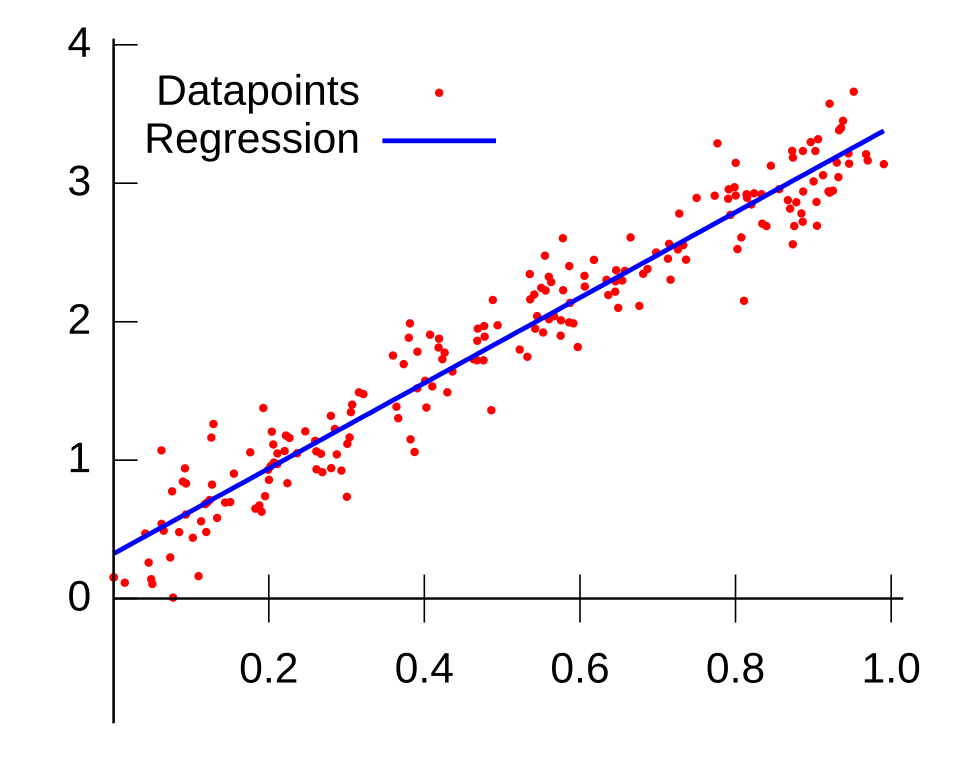
This figure shows a scatterplot of data points with a fitted least-squares regression line. The slope of the line summarizes the direction and strength of the linear relationship between the variables. In significance testing for the slope, the p-value indicates how unusual a slope at least this extreme would be if, in reality, there were no true linear relationship in the population. Source.

Why the p-Value Matters in Regression Analysis

The interpretation of the p-value forms the foundation for justifying conclusions in slope significance testing. Because regression seeks to generalize from sample patterns to population relationships, the p-value provides a standardized mechanism for evaluating whether observed trends likely reflect true underlying associations.