Understanding significant figures and maintaining numerical consistency are essential for ensuring experimental data and calculations reflect the true precision of measurements and support reliable, accurate scientific conclusions.

Understanding Significant Figures

Significant figures represent the digits in a measurement that are known with certainty plus one estimated digit. They convey the precision of a measurement and help ensure that reported data does not imply greater accuracy than the measuring instrument allows.

When performing calculations, significant figures must be handled correctly to maintain consistency and prevent errors caused by overstating or understating precision.

Why Significant Figures Matter

The proper use of significant figures ensures numerical consistency — results are expressed in a way that matches the accuracy of the input data and the measuring apparatus. Using too many digits can give a false impression of certainty, while using too few can reduce the usefulness of data.

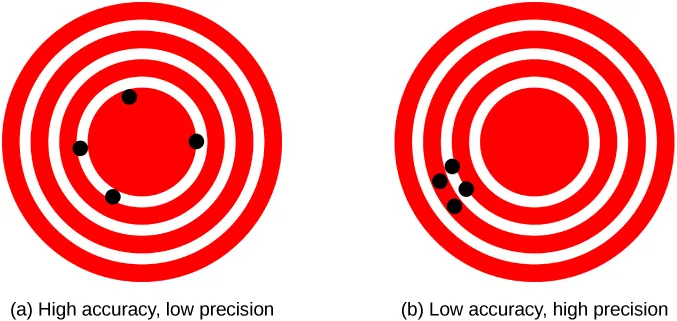
Target diagrams contrast high accuracy/low precision with low accuracy/high precision. These ideas explain why we limit reported digits: the precision of data and the accuracy of measurement determine how many significant figures are justified. Note: the figure introduces accuracy/precision explicitly, which is supportive background to sig-fig usage. Source

Scientific communication relies on accurate representation of precision. For example, stating a measurement as 1.20 m instead of 1.2 m implies that the measurement is known to the nearest centimetre rather than the nearest decimetre.

Rules for Counting Significant Figures

The number of significant figures in a value depends on the type of digits present.

Digits highlighted in colour indicate the significant figures; uncoloured digits are not significant. The examples illustrate when zeros count (e.g., trapped zeros) and when they do not (e.g., leading zeros). This visual aligns with the standard rules used in A-Level practical data reporting. Source

The following rules govern how significant figures are counted:

• All non-zero digits are significant. Example: 237 has three significant figures.

• Zeros between non-zero digits are significant. Example: 2.07 has three significant figures.

• Leading zeros (before the first non-zero digit) are not significant. Example: 0.0043 has two significant figures.

• Trailing zeros in a number with a decimal point are significant. Example: 3.200 has four significant figures.

• Trailing zeros in a whole number without a decimal point may or may not be significant — scientific notation clarifies this ambiguity.

Using Significant Figures in Calculations

Maintaining correct significant figures during calculations is crucial to ensure the propagation of precision aligns with measurement accuracy.

Multiplication and Division

When multiplying or dividing values:

• The result should have the same number of significant figures as the value with the fewest significant figures in the calculation.

Addition and Subtraction

When adding or subtracting values:

• The result should have the same number of decimal places as the value with the fewest decimal places.

These rules prevent misleading results where the final answer appears more precise than the least accurate measurement allows.

Rounding to Significant Figures

Rounding ensures results reflect the correct degree of precision:

• If the digit after the last significant figure is 5 or greater, round up.

• If it is less than 5, round down.

• Always round only at the final step of a multi-step calculation to avoid rounding errors.

Intermediate rounding can accumulate error, leading to results that deviate from the correct value. Numerical consistency depends on postponing rounding until the final stage.

Numerical Consistency

Numerical consistency refers to maintaining coherent precision throughout all stages of measurement, analysis, and reporting. Every number presented — whether a measurement, calculated value, or constant — should match the level of precision justified by the data.

Inconsistent significant figures can undermine confidence in results and indicate poor experimental practice. For example, combining 3.2 (two significant figures) with 3.245 (four significant figures) must yield a result rounded appropriately to maintain consistency.

Maintaining numerical consistency requires that the reported precision matches the actual limits of measurement accuracy. This principle applies equally to raw data, processed results, and final conclusions.

Role of Uncertainty in Significant Figures

Every measurement carries an uncertainty, which dictates the number of meaningful digits that can be justified.

A dial vernier caliper measuring length to fine increments demonstrates how instrument resolution sets the maximum significant figures in a result. The last recorded digit is the first uncertain one, and should be reported consistently with the tool’s precision. This directly underpins uncertainty statements such as ±(half a scale division). Source

EQUATION
—-----------------------------------------------------------------
Percentage Uncertainty (%) = (Absolute Uncertainty / Measured Value) × 100
Absolute Uncertainty = Estimate of possible error in a measurement, in the same units as the value measured
Measured Value = The recorded numerical result of a measurement
—-----------------------------------------------------------------

The uncertainty value determines how many significant figures should be reported. A measurement with a high relative uncertainty should be quoted with fewer significant figures than one with low relative uncertainty.

Consistency in Reporting Calculations

When reporting calculations:

• All raw measurements should be recorded with their appropriate number of significant figures.

• Calculated quantities should retain consistent precision based on the input data.

• Constants used (e.g., g = 9.81 m s⁻²) should have appropriate precision relevant to the context of the calculation.

• Final results should display the correct number of significant figures, and any units must be clearly stated.

Maintaining this discipline supports reproducibility and ensures others can interpret and verify results confidently.

Common Errors and Good Practice

To achieve high-quality, reliable data representation, students should avoid these frequent mistakes:

• Reporting too many digits after performing calculations.

• Mixing decimal places and significant figures inconsistently.

• Ignoring the influence of uncertainty on precision.

• Rounding at multiple intermediate stages.

• Presenting inconsistent figures across data tables and graphs.

Good practice includes:

• Writing all measurements to the same decimal place where appropriate.

• Recording uncertainties clearly.

• Ensuring that any calculated means, gradients, or derived quantities respect the least precise data input.

• Checking that all figures in a report align with the expected experimental precision.

Applying Significant Figures in Graphs and Tables

When presenting data graphically or in tables:

• Include units in column headings.

• Keep numerical values consistent in precision across rows and columns.

• Express calculated gradients or intercepts using an appropriate number of significant figures, matching the accuracy of plotted data.

• Avoid mixing overly precise and imprecise values within a single dataset.

By doing so, students reinforce both numerical consistency and the scientific integrity of their reported results.