OCR Specification focus:
‘Simple harmonic motion satisfies a = −ω²x; determine period or frequency using practical techniques.’
Simple harmonic motion (SHM) describes a fundamental type of oscillation where acceleration and displacement are directly related and always act in opposite directions. Understanding this defining equation and measuring oscillatory quantities underpin much of wave and vibration physics.
The Defining Equation of Simple Harmonic Motion
In simple harmonic motion, an object’s acceleration is proportional to its displacement from a fixed equilibrium position and directed towards that equilibrium. This relationship defines SHM mathematically and conceptually.
Simple Harmonic Motion: Motion in which the acceleration of an object is directly proportional to its displacement from a fixed equilibrium point and acts towards that point.
This means that when a system is displaced, it experiences a restoring acceleration that tries to bring it back to equilibrium.
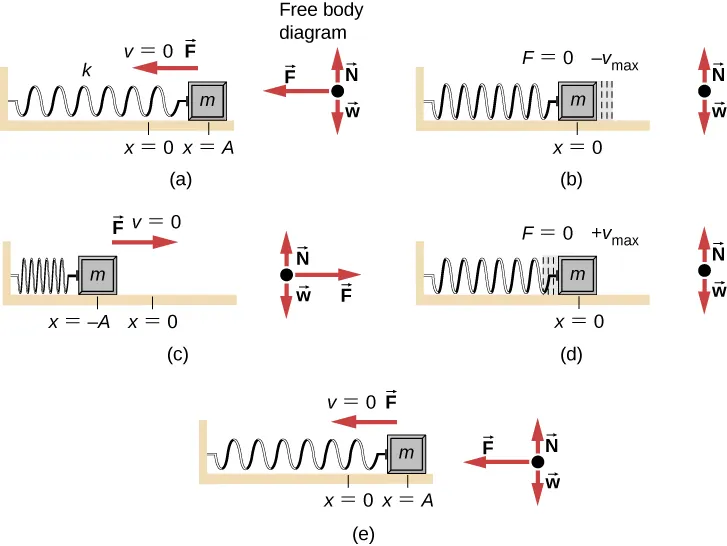
Mass–spring oscillator at various positions, with forces indicated by vectors. The restoring force reverses direction with displacement and is proportional to distance from equilibrium, illustrating the defining SHM relationship a=−ω2xa = -\omega^{2}xa=−ω2x. Source.
EQUATION
—-----------------------------------------------------------------
Defining Equation of SHM (a) = −ω²x
a = Acceleration of the object (m s⁻²)
ω = Angular frequency (rad s⁻¹)
x = Displacement from equilibrium (m)
—-----------------------------------------------------------------
The negative sign indicates that the acceleration is always in the opposite direction to displacement — a restoring effect that maintains oscillation. The larger the displacement, the greater the restoring acceleration, ensuring the system continues oscillating about the equilibrium position.
Physical Meaning of the Defining Equation
The defining equation reveals several important characteristics of SHM:
Restoring nature: The force or acceleration always acts towards the equilibrium point, creating oscillatory motion.
Proportional relationship: The magnitude of acceleration increases linearly with displacement.
Dependence on angular frequency: Systems with higher angular frequency oscillate faster and have greater acceleration for a given displacement.
These principles apply to many systems, such as a mass–spring oscillator or a pendulum undergoing small angular displacements.
Connecting Force and Acceleration in SHM
Newton’s Second Law (F = ma) allows the defining equation to be rewritten in terms of force, showing the physical mechanism of oscillation.
EQUATION
—-----------------------------------------------------------------
Restoring Force in SHM (F) = −mω²x
F = Restoring force acting on the system (N)
m = Mass of the oscillating object (kg)
ω = Angular frequency (rad s⁻¹)
x = Displacement from equilibrium (m)
—-----------------------------------------------------------------
This expression highlights that the restoring force is proportional to displacement and always acts towards equilibrium. Such forces are central to all harmonic oscillators, whether mechanical or electrical.
Determining Period and Frequency in SHM
The period (T) and frequency (f) describe how quickly oscillations occur. These can be determined using theoretical relations or practical measurement techniques.
Period (T): The time taken for one complete oscillation, measured in seconds (s).
Frequency (f): The number of complete oscillations per second, measured in hertz (Hz).
The defining equation of SHM relates directly to angular frequency, which connects to these measurable quantities.
EQUATION
—-----------------------------------------------------------------
Angular Frequency (ω) = 2π/T = 2πf
ω = Angular frequency (rad s⁻¹)
T = Period (s)
f = Frequency (Hz)
—-----------------------------------------------------------------
Using these relationships, we can determine ω — and hence describe the motion mathematically — once either period or frequency is known.
Experimental Measurement of Period and Frequency
Practical measurement of oscillatory motion is essential in physics laboratories. Several reliable techniques exist for different systems:
Measuring Period Using a Stopwatch
For slow oscillations such as a pendulum:
Displace the oscillator slightly and release it without pushing.
Start timing when it passes the equilibrium point in one direction.
Count a large number (e.g. 10 or 20) of complete oscillations to reduce random error.
Divide the total time by the number of oscillations to calculate the mean period (T).
This method provides sufficient accuracy when oscillations are slow and clearly visible.
Using a Data Logger or Light Gate
For faster oscillations such as a mass–spring system:
Attach a reflective marker or interrupt card to the oscillating mass.
Position a light gate connected to a data logger to detect each pass through equilibrium.
The logger records time intervals automatically, producing precise values for T.
Such digital techniques reduce human error and provide high-resolution timing data.
Using an Oscilloscope for Electrical Oscillations
For alternating current (AC) or vibrating systems that produce electrical signals:
Connect the oscillator output to an oscilloscope.
Measure the time base interval between successive identical points on the waveform (e.g. peaks).
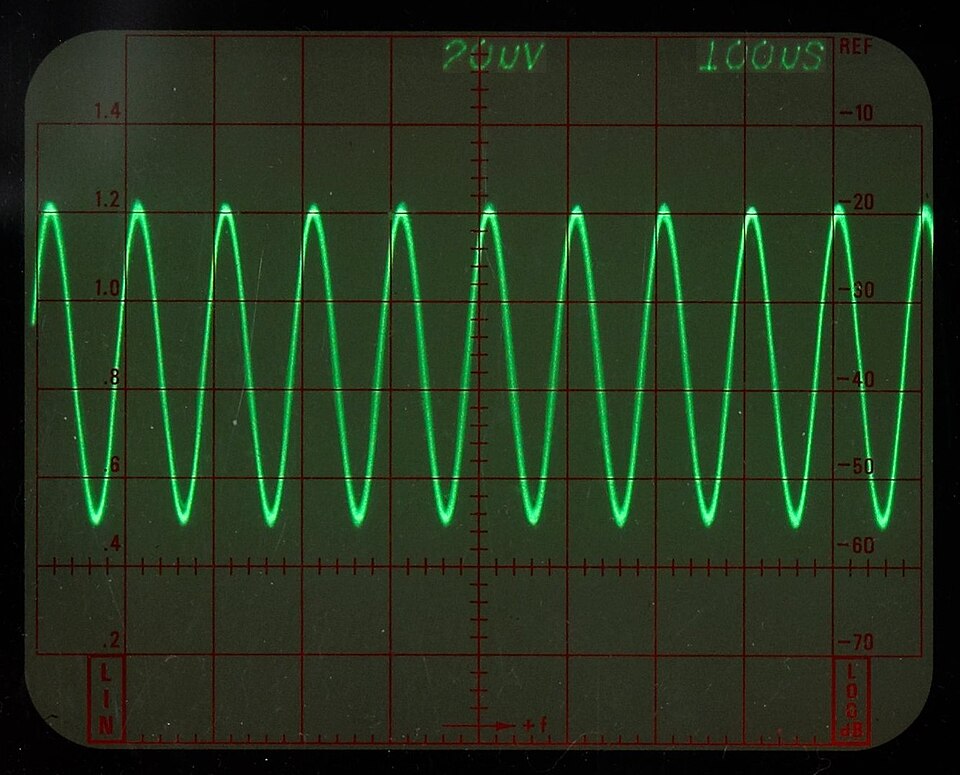
Analogue oscilloscope display of a sinusoidal signal. The horizontal graticule enables direct measurement of the period TTT between peaks, from which frequency fff is calculated. The clearly resolved waveform allows accurate timing using grid or cursors. Source.
This interval represents the period T, from which f = 1/T can be calculated.
Oscilloscopes are particularly useful for studying electrical oscillators, signal generators, or resonant circuits.
Accuracy and Sources of Error
Accurate measurement of oscillatory motion requires minimising both random and systematic errors. Important considerations include:
Amplitude consistency: Keep amplitude small for systems approximating SHM, such as pendulums, to ensure linear restoring force.
Timing precision: Use multiple oscillations to average timing errors.
Environmental factors: Air resistance and friction introduce damping, which slightly alters the observed period.
Calibration: Verify instruments like light gates or oscilloscopes before use to ensure timing accuracy.
These measures improve the reliability of the determined period (T) or frequency (f).
Linking Measurement to the Defining Equation
Once ω is found experimentally using ω = 2π/T, it can be substituted into the defining equation a = −ω²x to predict acceleration at different displacements. Comparing these predicted accelerations with measured values allows verification of SHM behaviour.
For example:
Plotting acceleration (a) against displacement (x) for measured data should yield a straight line through the origin with gradient −ω².
This linear relationship experimentally confirms that acceleration is proportional to displacement and directed oppositely, verifying the defining equation.
Key Takeaways on the Defining Equation and Measurement
Understanding and measuring the relationship between acceleration, displacement, and angular frequency lies at the heart of SHM analysis. The defining equation, a = −ω²x, not only describes how oscillations behave but also provides a framework for experimental verification using precise measurement of period or frequency. Through careful practical methods, physicists validate the fundamental nature of oscillatory motion and its elegant mathematical symmetry.
FAQ
To verify the equation, you can measure both acceleration and displacement for a simple harmonic oscillator, such as a mass on a spring.
Use a motion sensor or data logger to record displacement over time.
Differentiate the displacement data twice to obtain acceleration.
Plot acceleration (a) against displacement (x).
If the motion is simple harmonic, the graph should be a straight line through the origin with a negative gradient equal to −ω². This confirms that acceleration is proportional to displacement and directed towards equilibrium.
The negative sign indicates that the acceleration always acts in the opposite direction to the displacement from equilibrium.
If the object is displaced to the right (positive x), acceleration acts to the left (negative direction), and vice versa. This restoring nature ensures the system oscillates about its equilibrium position rather than moving indefinitely away from it.
Without the negative sign, the motion would not return to equilibrium, and no oscillation would occur.
For motion to be perfectly simple harmonic, certain ideal conditions must apply:
The restoring force must be directly proportional to displacement.
The amplitude must be small enough that this proportionality remains linear.
Frictional and resistive forces must be negligible (no damping).
In real systems, these assumptions are approximations. Large amplitudes or friction cause deviations from true SHM, resulting in non-linear motion or gradual energy loss.
Angular frequency depends on the restoring force mechanism and the system’s inertia.
For a mass–spring system, ω = √(k/m), where k is the spring constant and m is the mass.
For a simple pendulum, ω = √(g/L), where g is the gravitational field strength and L is the pendulum length.
Thus, ω increases with stronger restoring forces or shorter pendulums, and decreases with greater mass or length. These relations allow direct calculation of period and frequency from measurable quantities.
Several experimental factors influence timing precision:
Human reaction time: Use a photogate or data logger instead of a manual stopwatch.
Amplitude variation: Keep amplitude small and consistent between oscillations.
Environmental effects: Air resistance and friction introduce damping, changing the apparent period.
Instrument calibration: Ensure sensors and timers are correctly zeroed and synchronised.
Minimising these errors is essential for obtaining accurate values of T, f, and subsequently ω in the defining SHM equation.
Practice Questions
Question 1 (2 marks)
A mass oscillates on a spring in simple harmonic motion. At a displacement of 0.04 m from equilibrium, the acceleration of the mass is 1.6 m s⁻² towards the equilibrium position.
(a) Calculate the angular frequency of the motion.
Mark scheme:
• Substitution into the defining equation a = −ω²x (1 mark)
• Correct calculation: ω² = a/x = 1.6 / 0.04 = 40, hence ω = 6.32 rad s⁻¹ (accept 6.3) (1 mark)
Question 2 (5 marks)
Describe how you could determine the period and hence the frequency of a simple pendulum undergoing small oscillations. Explain how your measurements and analysis would confirm that the pendulum performs simple harmonic motion.
Mark scheme:
• Method: displace pendulum slightly from equilibrium and release without push (1 mark)
• Measure the time for multiple oscillations using a stopwatch or photogate/data logger to reduce random error (1 mark)
• Calculate mean period T = total time / number of oscillations (1 mark)
• Determine frequency using f = 1/T (1 mark)
• Confirmation of SHM: acceleration proportional to displacement and directed towards equilibrium, e.g. by plotting a against x to give a straight line through origin with gradient −ω² (1 mark)

