OCR Specification focus:
‘Discuss practical examples of forced oscillations and resonance across different systems.’
Resonance appears in many natural and engineered systems, producing greatly increased oscillation amplitude when a driving frequency matches a system’s natural frequency. Understanding real examples helps reveal resonance’s usefulness and potential risks in practical contexts facing physicists and engineers.
Resonance in Mechanical Structures
Mechanical systems often possess well-defined natural frequencies. When an external periodic force — such as wind, footsteps or engine vibrations — acts near these frequencies, resonance can dramatically increase oscillatory motion.
Resonance: The phenomenon in which an oscillating system experiences a maximum amplitude when the driving frequency matches the system’s natural frequency.
Structures are designed to tolerate oscillations, but under resonant conditions their response may become dangerous. Engineers therefore work to identify possible vibrational modes before construction.
Bridges and Walkways
Bridges are classic examples in resonance discussions because their natural frequencies can coincide with repeated external forcing.
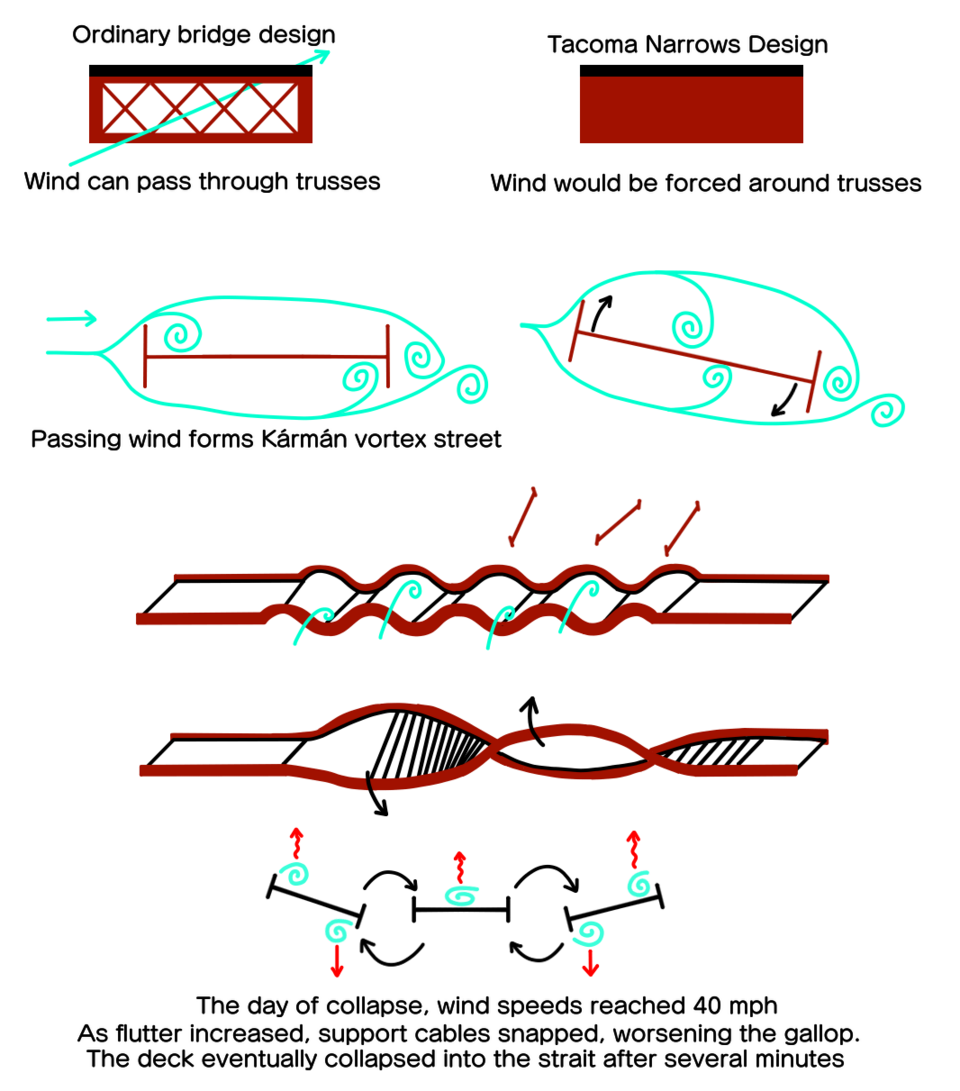
Simplified representation of the Tacoma Narrows Bridge undergoing large-amplitude oscillations during its 1940 collapse, illustrating how wind forcing can drive a structure at its natural frequency to produce destructive resonance. Source.
Students should recognise the following key points:
Pedestrian-induced forcing can occur when walkers inadvertently synchronise their steps.
Wind-induced forcing may supply periodic energy to suspension cables or decking.
Vehicle-induced vibrations can drive oscillation when mass and spacing create rhythmic loading.
To mitigate risk, engineers use:
Damping mechanisms such as tuned mass dampers and viscous dampers
Structural stiffening to shift natural frequencies
Design monitoring to detect unwanted oscillations
These measures prevent the excessive amplitudes that resonance can produce.
Tall Buildings
Skyscrapers behave like tall oscillators with multiple vibrational modes. Wind buffeting acts as a periodic driving force.
Key ideas:
Resonant swaying can cause discomfort even when structurally safe.
Tuned mass dampers help reduce motion by providing counter-oscillations.
Frequency engineering ensures natural frequencies avoid common wind-excitation ranges.
A sentence before using any further definition ensures clear spacing between informational elements.
Natural Frequency: The frequency at which a system oscillates when displaced and released without external forcing.
Electrical Resonance in AC Circuits
Oscillatory behaviour is not limited to mechanical systems. Electrical circuits with inductors and capacitors form systems that resonate when driven by an alternating current.
Resonant LC Circuits
LC circuits have a natural frequency determined by inductance and capacitance.
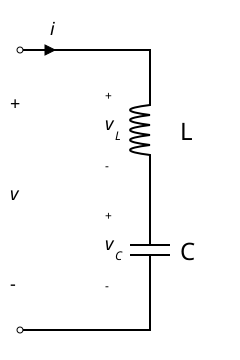
Schematic of a series LC circuit showing the arrangement that produces electrical resonance when the driving frequency equals the natural frequency set by inductance and capacitance. Source.
When the driving frequency of an AC source equals this natural frequency, the circuit responds with a large alternating current.
EQUATION
—-----------------------------------------------------------------
Resonant Frequency (f₀) = 1 / (2π√(LC))
f₀ = Resonant frequency in hertz (Hz)
L = Inductance in henry (H)
C = Capacitance in farad (F)
—-----------------------------------------------------------------
Resonant electrical circuits are widely used because their selectivity allows them to respond strongly only to desired frequencies.
After considering the equation, it is important to note how such resonance is used in practical devices.
Radio and Communication Systems
Radio receivers depend on resonance to isolate a single broadcasting frequency. The tuning dial varies capacitance or inductance to adjust the natural frequency of an LC circuit.
Important features:
Selecting one station requires narrow-band resonance.
Adjusting the circuit’s natural frequency allows matching to the desired driving frequency.
Undesired frequencies produce only small currents because they are far from resonance.
Resonant circuits thus perform as frequency selectors in communication technologies.
Acoustic Resonance
Resonance also governs many sound-producing systems where air columns or physical bodies vibrate.
Musical Instruments
Musical instruments rely on acoustic resonance to amplify certain frequencies.
Mechanisms include:
Strings or air columns forcing the body of the instrument to vibrate.
Standing waves forming at specific natural frequencies.
Harmonics and overtones emerging from resonant modes.
For wind instruments, the length of the air column determines resonant frequencies. For stringed instruments, the tension, mass per unit length and effective length of the string influence natural oscillations.
A short sentence ensures spacing before another definition block appears.
Forced Oscillation: Oscillatory motion that occurs because a system is driven by an external periodic force rather than oscillating freely.
Human Hearing and Resonance
The human ear canal itself demonstrates resonance, enhancing sensitivity to frequencies near its natural mode. This amplification helps perception of speech frequencies.
Key points include:
The ear canal behaves like a closed tube resonator.
Resonance increases sound intensity at characteristic frequencies.
Understanding this aids design of hearing protection and audio equipment.
Resonance in Everyday Technology
Microwave Ovens
Microwaves deliver energy at a frequency that resonates with rotational modes of water molecules. This resonance enables efficient heating.
Quartz Timekeeping
Quartz crystals exhibit mechanical resonance due to their piezoelectric properties. When driven electrically at the crystal’s natural frequency, they oscillate with remarkable stability, enabling accurate timekeeping.
Main features:
Stable resonant frequency maintains consistent oscillations.
Electronic feedback keeps the crystal driven at resonance.
Precision arises from minimal energy loss and high Q-factor.
Automotive Systems
Car suspension systems can resonate due to road-induced periodic forces. Shock absorbers provide damping so resonance does not create uncomfortable or unsafe motion.
Bullet points to reinforce key contexts:
Tyre imbalance produces periodic forcing.
Correct damping reduces resonant oscillations.
Engineering design avoids natural frequencies associated with typical road-vibration frequencies.
These examples emphasise resonance as a fundamental principle across mechanical, electrical and acoustic systems, aligning with the OCR specification’s emphasis on forced oscillations and resonance in real applications.
FAQ
A system is most susceptible to resonance when it has very low damping, meaning it loses little energy per cycle. This allows oscillations to build up rapidly when driven at the natural frequency.
Other factors include:
A narrow resonance peak, so even small changes in driving frequency produce large amplitude changes.
Structural symmetry, which can support strong vibrational modes.
External forces that act regularly or periodically, such as wind or rotating machinery.
Resonance can be highly advantageous when controlled. When the natural frequency is known and safely managed, resonance can amplify desirable effects.
Examples include:
Maximising efficiency in radio-frequency filters and tuning circuits.
Enhancing signal detection in sensors such as quartz oscillators.
Producing stronger sound in musical instruments by resonating air columns or bodies.
Control methods such as damping or frequency locking ensure resonance remains safe.
Even a small periodic force can produce a large response because energy is added every cycle in phase with the oscillation, allowing energy to accumulate.
This accumulation continues until:
Damping balances the input energy, setting a steady amplitude.
Structural limits are reached, which may cause damage.
The key is the synchronisation between the driving force and the oscillator, which leads to constructive reinforcement.
The dominant mode of resonance depends on the bridge’s geometry, mass distribution and structural stiffness.
Different modes arise because:
Vertical modes relate to deck flexing.
Lateral modes involve sideways movement from asymmetric wind loading.
Torsional modes occur when the two sides of the deck twist relative to one another.
Wind direction, pedestrian movement patterns and vehicle loads can selectively excite one of these modes.
Although both rely on matching the driving frequency to the natural frequency, the way energy is stored differs between systems.
In mechanical systems:
Energy alternates between kinetic energy of motion and potential energy in deformation (e.g., bending or stretching).
In electrical LC circuits:
Energy oscillates between the magnetic field of the inductor and the electric field of the capacitor.
In both cases, resonance maximises the rate at which energy is transferred into the oscillator from the external driver.
Practice Questions
Question 1 (2 marks)
Give one practical example of resonance in an engineered structure and explain why the amplitude of oscillation becomes large in this situation.
Question 1 (2 marks)
1 mark for identifying a correct practical example (e.g., Tacoma Narrows Bridge, pedestrian-induced resonance on footbridges, tall building swaying, car suspension, quartz crystal oscillators).
1 mark for explaining that amplitude increases because the driving frequency matches the natural frequency, resulting in maximum energy transfer.
Question 2 (5 marks)
A student is investigating practical examples of resonance in different physical systems.
(a) Describe how resonance occurs in a series LC circuit used in radio tuning.
(b) Explain why resonance can be both useful and potentially hazardous in real-world applications, referring to at least one mechanical and one electrical example.
Question 2 (5 marks)
(a)
1 mark for stating that resonance occurs when the driving frequency of the AC source equals the natural frequency of the LC circuit.
1 mark for explaining that at resonance, current in the circuit becomes large due to minimal impedance.
(b)
1 mark for explaining a useful application (e.g., resonance allows radio receivers to select a specific station by tuning an LC circuit to one frequency).
1 mark for explaining a potential hazard in mechanical systems (e.g., bridges or buildings can experience dangerously large oscillations when forced at their natural frequencies).
1 mark for giving a clear comparison or linking statement showing understanding that resonance leads to large-amplitude oscillations which may be helpful or harmful depending on context.

