In experimental physics, precision and accuracy describe the quality and reliability of measurements. Understanding these concepts ensures that data interpretation and conclusions drawn from experiments are scientifically valid and trustworthy.

Understanding Measurement Quality

When making measurements in physics, it is crucial to assess how close the results are to the true value and how consistent repeated measurements are. These two characteristics define the accuracy and precision of the measurement process. Both are essential in evaluating the validity of experimental data, but they describe different aspects of measurement performance.

Accuracy

Accuracy reflects how close a measurement is to the true or accepted value of the quantity being measured. An accurate measurement has minimal systematic error, meaning the measuring instrument or method consistently gives results close to the true value.

An accurate measurement can be achieved through:

• Properly calibrated instruments that read zero correctly.

• Eliminating systematic errors, such as parallax or instrument bias.

• Correct experimental technique and proper use of measuring devices.

Inaccurate measurements are often caused by systematic errors, which shift all data points by a consistent amount or proportion. For example, a miscalibrated ammeter reading 0.1 A too high across all measurements will yield inaccurate results, even if the readings appear consistent.

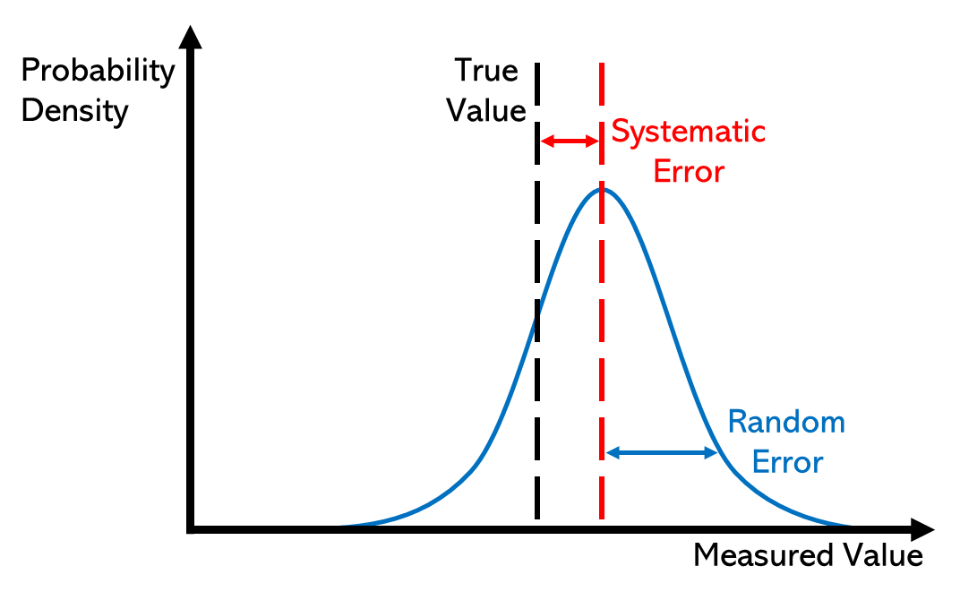
Probability density curves illustrating random error as width (blue) and systematic error as a constant shift from the true value (red). The blue distribution is centred but broad; the red is narrow but displaced. This clarifies why precision can be high while accuracy is poor, and vice versa. Source.

Precision

Precision describes the consistency or repeatability of measurements. If repeated readings of the same quantity give results that are very close together, the measurements are said to be precise. Precision does not depend on how close the results are to the true value.

A precise set of readings indicates low random error. Precision depends on:

• The sensitivity and resolution of the measuring instrument.

• The control of experimental variables (temperature, vibration, etc.).

• The skill of the experimenter in performing consistent measurements.

For example, if a micrometer consistently reads 5.01 mm, 5.02 mm, and 5.00 mm for a true value of 5.10 mm, the measurements are precise but not accurate.

Comparing Accuracy and Precision

Although closely related, accuracy and precision assess different properties:

• Accuracy concerns closeness to truth.

• Precision concerns closeness to each other.

It is possible for data to be:

• Accurate but not precise – individual measurements cluster around the true value but are widely spread.

• Precise but not accurate – measurements are consistent but systematically offset from the true value.

• Neither accurate nor precise – scattered results far from the true value.

• Both accurate and precise – consistent and close to the true value, representing high-quality data.

A good experiment aims for both high accuracy and high precision.

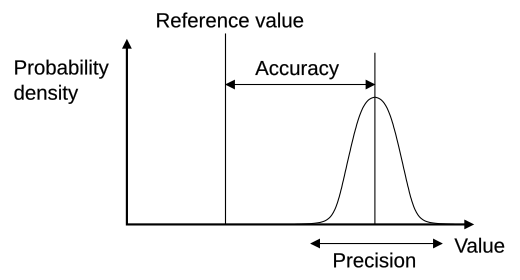
A four-panel target diagram contrasting accuracy and precision. Shots clustered tightly but offset illustrate high precision, low accuracy, while shots spread widely around the centre show low precision. This visual reinforces the independent meanings of the two terms. Source.

Factors Affecting Accuracy and Precision

Sources Influencing Accuracy

Accuracy can be reduced by:

• Systematic errors such as instrument calibration faults or environmental effects (e.g. temperature drift).

• Incorrect zeroing of measuring instruments.

• Consistent parallax errors from improper reading positions.

• Faulty theoretical assumptions or limitations in experimental design.

Improving accuracy often involves:

• Calibrating instruments against known standards.

• Applying correction factors for known biases.

• Using appropriate measuring ranges for instruments.

Sources Influencing Precision

Precision depends mainly on:

• Random errors, caused by unpredictable variations in measurements.

• Instrument resolution, the smallest detectable change in quantity.

• Experimental control, such as maintaining constant temperature or stable equipment positioning.

• Number of repeated trials, since averaging multiple readings reduces random uncertainty.

To improve precision:

• Use high-resolution instruments.

• Conduct multiple trials and calculate mean values.

• Minimise environmental fluctuations and improve measurement technique.

Role of Uncertainty in Precision and Accuracy

In measurement science, both accuracy and precision contribute to the uncertainty associated with a result. A small uncertainty suggests a precise measurement, but not necessarily an accurate one. The uncertainty range provides a numerical indication of the spread or confidence in data.

While precision is linked to the size of random uncertainty, accuracy is influenced by systematic uncertainty. Therefore, reporting both the measured value and its uncertainty allows a more complete representation of measurement quality.

Representation of Precision and Accuracy in Data

When presenting data:

• Accurate data will align closely with the expected theoretical relationship.

• Precise data will exhibit small scatter around the line of best fit on a graph.

• Large scatter implies poor precision, while consistent deviation from the true trend indicates poor accuracy.

In a laboratory setting, students should:

• Record all measurements with appropriate significant figures to reflect instrument precision.

• Use error bars on graphs to represent uncertainty.

• Comment on both accuracy and precision when discussing the reliability of results.

Summary of Key Distinctions

• Accuracy improves by reducing systematic errors.

• Precision improves by reducing random errors.

• Calibration and standardisation enhance accuracy.

• Repetition and averaging enhance precision.

• Accurate and precise measurements produce the most reliable and valid experimental conclusions.

By understanding and applying the principles of accuracy and precision, students can critically evaluate data quality, enhance measurement reliability, and demonstrate mastery of good scientific practice.