OCR Specification focus:
‘Calculate absolute and percentage uncertainties when combining data by addition or subtraction.’
Understanding how uncertainties combine during addition and subtraction of measurements is vital in experimental physics, ensuring data is expressed with realistic precision and reliability in final results.
Understanding Uncertainty in Measurements
Every physical measurement carries an uncertainty, a reflection of the limitations of instruments and methods used in experimental work. Recognising and managing these uncertainties allows scientists to evaluate the reliability of their conclusions. Uncertainty is not error; rather, it quantifies the range within which the true value is expected to lie.
Uncertainty: The estimated range within which the true value of a measured quantity lies, reflecting the precision of the measurement.
When combining data from multiple measurements, the associated uncertainties must also be combined appropriately, depending on the mathematical operation performed. The OCR specification emphasises this for addition and subtraction of data, requiring students to calculate absolute and percentage uncertainties in results derived from such combinations.
Absolute Uncertainty and Its Role
Absolute uncertainty expresses the actual size of the possible error in the same units as the measured quantity. It provides a direct measure of the margin of doubt around a measurement.
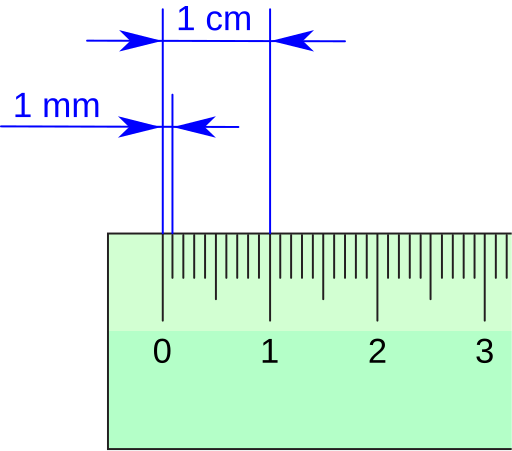
Close, uncluttered view of centimetre and millimetre graduations on a ruler. For a ruler with 1 mm smallest division, a typical reading uncertainty is of order ±0.5 mm, reported in the same units as the measurement. This directly supports quoting absolute uncertainties before combining by addition or subtraction. Source.
Absolute uncertainty: The uncertainty in a measurement expressed in the same units as the measurement itself (e.g. ±0.2 m or ±0.05 s).
For example, a length measured as 2.40 ± 0.05 m means the true value likely lies between 2.35 m and 2.45 m. Absolute uncertainties are particularly useful when combining measurements through addition or subtraction, as these operations affect the total error range directly.
Combining Uncertainties in Addition and Subtraction
When quantities are added or subtracted, their absolute uncertainties combine according to a straightforward rule:
the total absolute uncertainty equals the sum of the absolute uncertainties of the individual quantities.
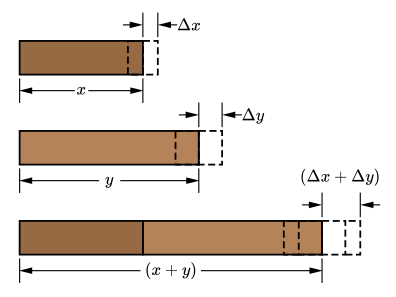
Diagram showing two measured lengths with their uncertainty ranges and the resulting sum with a larger combined absolute uncertainty. This visual reinforces that, for addition and subtraction, uncertainties add irrespective of the sign of the operation. Labels are minimal, keeping focus on the rule required by the specification. Source.
EQUATION
—-----------------------------------------------------------------
Combined Absolute Uncertainty (ΔR) = ΔA + ΔB (+ ΔC …)
ΔR = absolute uncertainty in the result
ΔA, ΔB, ΔC = absolute uncertainties in the individual quantities
—-----------------------------------------------------------------
This rule applies regardless of whether quantities are being added or subtracted, because subtraction affects the result’s value but not the spread of uncertainty. The key principle is that each individual uncertainty contributes to the overall possible variation in the result.
For instance, if a displacement is calculated as the difference between two position measurements, each position measurement’s uncertainty must be accounted for by summing their absolute uncertainties. This reflects the realistic combined range of possible error in the calculated displacement.
Why Uncertainties Add in This Way
The process of combining absolute uncertainties by summation assumes a worst-case scenario—that all uncertainties act in the same direction to produce the largest possible deviation. This ensures results remain conservatively reliable, preventing overconfidence in the precision of the outcome.
Even though in practice random variations might cancel each other to some extent, physics at the A-Level stage prioritises simplified and safe estimates, ensuring all potential sources of inaccuracy are represented.
Key Points
When adding quantities, uncertainties add together.
When subtracting quantities, uncertainties still add together.
This rule applies to absolute uncertainties, not percentage uncertainties.
The units of the combined uncertainty are the same as the measured quantities.
These principles make it possible to represent a derived measurement with a final value and total uncertainty that properly account for all measurement sources.
Percentage Uncertainty in Combined Measurements
To compare uncertainties between different measurements, or to express them in relative terms, scientists often use percentage uncertainty. This shows the uncertainty as a proportion of the measured value.
Example error-bar graph with means and vertical intervals, illustrating how uncertainty is presented relative to a plotted value. While these bars represent 95% confidence intervals (extra detail beyond the syllabus), the key takeaway is that an interval communicates the size of uncertainty about each point. Use the same idea when reporting percentage uncertainties. Source.
Percentage uncertainty: The absolute uncertainty divided by the measured value, multiplied by 100%.
Once the absolute uncertainty of a combined measurement (from addition or subtraction) has been found, it can be converted into a percentage uncertainty to indicate the reliability of the final value.
EQUATION
—-----------------------------------------------------------------
Percentage Uncertainty (%) = (Absolute Uncertainty ÷ Measured Value) × 100
Absolute Uncertainty = combined uncertainty in the same units as the result
Measured Value = final result of the addition or subtraction
—-----------------------------------------------------------------
This representation allows quick comparison between measurements of different magnitudes, identifying which contributes most to the overall inaccuracy. A small absolute uncertainty can still correspond to a large percentage uncertainty if the measured value is small.
Managing Uncertainties in Practical Work
In experimental situations, reducing uncertainty requires careful technique and appropriate instruments. However, when combining data, following consistent methods ensures uncertainties are not underestimated or misrepresented.
When measurements are combined:
Always convert all values to the same units before calculating uncertainties.
Add absolute uncertainties directly when quantities are summed or subtracted.
Report the final value with its combined uncertainty using correct significant figures.
Convert to percentage uncertainty when comparing the reliability of different results.
Ensure that uncertainty propagation aligns with the operation performed — addition/subtraction versus multiplication/division (the latter handled in a separate subsubtopic).
Practical Considerations
When one uncertainty is much larger than others, it dominates the total combined uncertainty.
Repeating measurements and averaging can reduce random uncertainty, but systematic errors remain unless identified and corrected.
It is standard to quote the final result as:
Quantity = Value ± Uncertainty (with units).
Importance for Experimental Physics
The skill of calculating uncertainties accurately ensures that data analysis and conclusions remain scientifically defensible. Whether determining reaction times, resistances, or velocities, combining uncertainties correctly shows how confident one can be in the result.
In professional physics, this understanding extends to error propagation theory, but for OCR A-Level students, mastering the addition and subtraction of absolute uncertainties provides a foundational tool for clear and rigorous analysis.
FAQ
When more than two quantities are added or subtracted, all absolute uncertainties are summed together to give the total uncertainty.
For example, if you add three lengths A, B, and C, with uncertainties ΔA, ΔB, and ΔC, the total uncertainty is ΔA + ΔB + ΔC. This follows the same principle as with two quantities — each measurement contributes to the overall possible range of error.
This approach ensures that the final result represents the largest realistic range of values consistent with all measurement uncertainties.
Addition and subtraction involve quantities expressed in the same units (such as metres or seconds). Therefore, absolute uncertainty — expressed in those same units — gives a direct sense of the possible variation in the combined value.
Percentage uncertainty is more appropriate for multiplicative operations, where different magnitudes or units make direct addition of uncertainties meaningless.
In short:
Use absolute uncertainties for addition/subtraction.
Use percentage uncertainties for multiplication/division.
Uncertainty can be reduced by improving measurement precision before combining results. Methods include:
Using instruments with smaller scale divisions or higher resolution.
Repeating measurements and taking a mean to reduce random uncertainty.
Ensuring consistent calibration of instruments to avoid zero errors.
Recording readings carefully and consistently, reducing parallax or misalignment errors.
Reducing uncertainty before combining results ensures the final total uncertainty is smaller, improving confidence in the derived quantity.
The uncertainty should be given to one or two significant figures, and the measured value should be rounded to the same decimal place.
For example:
If a measurement is 12.63 ± 0.08 m, both are quoted to two decimal places.
Key points:
Never quote an uncertainty with more precision than the measurement allows.
This ensures the uncertainty reflects realistic precision, avoiding a misleading impression of accuracy.
OCR A-Level Physics emphasises conservative estimation over advanced statistical treatment. The rule of adding absolute uncertainties gives a worst-case scenario that’s simple, transparent, and suitable for practical work.
More sophisticated approaches, such as root-sum-square or propagation of uncertainty equations, are used in university-level studies where random and systematic components can be analysed separately.
At A-Level, the additive rule ensures all potential deviations are considered, reinforcing safe and realistic interpretation of results.
Practice Questions
Question 1 (2 marks)
A student measures the thickness of two glass plates before stacking them together.
Plate A: 4.20 ± 0.05 mm
Plate B: 2.60 ± 0.02 mm
Calculate the combined thickness and the total absolute uncertainty of the stacked plates.
Mark Scheme
Correct combined value: 4.20 + 2.60 = 6.80 mm (1 mark)
Correct total absolute uncertainty: 0.05 + 0.02 = 0.07 mm (1 mark)
Award both marks only if units are included correctly.
Question 2 (5 marks)
A physics student measures the distance between two points using two separate position readings:
Reading 1: 3.52 ± 0.02 m
Reading 2: 1.36 ± 0.01 m
(a) Determine the displacement between the two points and its absolute uncertainty. (2 marks)
(b) Calculate the percentage uncertainty in the displacement. (2 marks)
(c) Explain why the absolute uncertainties are added, even though the displacement involves subtraction of readings. (1 mark)
Mark Scheme
(a)
Correct displacement: 3.52 – 1.36 = 2.16 m (1 mark)
Correct absolute uncertainty: 0.02 + 0.01 = 0.03 m (1 mark)
(b)
Percentage uncertainty formula or correct reasoning shown: (Δx / x) × 100 (1 mark)
Correct value: (0.03 / 2.16) × 100 = 1.39% ≈ 1.4% (1 mark)
(c)
States that uncertainties are always added for both addition and subtraction because each measurement contributes to the total possible error range (1 mark)
Accept equivalent phrasing such as “uncertainties combine to show the full range of potential variation regardless of operation.”

