Understanding how to determine the resultant of two coplanar vectors is essential in physics, as it allows the analysis of combined effects of forces, velocities, or displacements acting in a single plane.

1. Understanding Coplanar Vectors

Vectors are quantities with both magnitude and direction. When two or more vectors lie in the same plane, they are described as coplanar vectors. This means their directions can be represented within a two-dimensional plane, such as the surface of a page.

In many physical situations—such as forces acting on an object resting on a slope or the velocity components of an aircraft in wind—only coplanar vectors are involved. Analysing these vectors accurately enables precise predictions of the resultant direction and magnitude.

2. The Concept of a Resultant Vector

When two or more vectors act simultaneously, their combined effect can be replaced by a single vector that produces the same effect. This vector is called the resultant vector.

The resultant does not alter the physical situation—it simply simplifies analysis by representing several vectors as one equivalent quantity.

3. Vector Addition in a Plane

The resultant of two coplanar vectors can be found using either geometrical or analytical methods. The vector triangle method is one of the most intuitive graphical approaches.

3.1 The Triangle of Vectors

In the triangle of vectors, the two vectors are drawn tip-to-tail, meaning the tail of the second vector starts at the tip of the first.

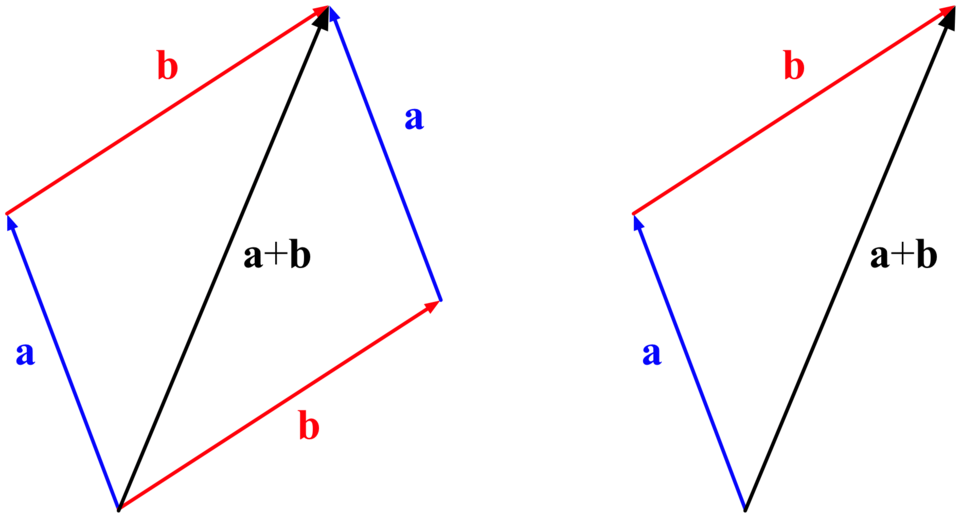
Tip-to-tail (triangle law) and parallelogram constructions for adding two vectors a and b. The resultant is the arrow drawn from the start of the first vector to the end of the second (or the diagonal of the parallelogram). These equivalent constructions are the standard graphical methods for two coplanar vectors. Source.

This construction relies on the triangle law of vector addition, which states that if two vectors are represented by two sides of a triangle taken in order, their resultant is given by the third side taken in the opposite order.

EQUATION
—-----------------------------------------------------------------
Resultant of Two Vectors (R) = √(A² + B² + 2AB cosθ)
R = Resultant magnitude (same unit as A and B)
A, B = Magnitudes of the two vectors
θ = Angle between the two vectors (degrees or radians)
—-----------------------------------------------------------------

The direction of the resultant relative to one of the vectors is found using trigonometric relationships, specifically the sine rule.

EQUATION
—-----------------------------------------------------------------
Sine Rule for Resultant Direction: (sin α)/B = (sin β)/A = (sin θ)/R
α, β = Angles opposite sides A and B respectively
θ = Included angle between A and B
—-----------------------------------------------------------------

4. Analytical Determination of Resultant

Beyond geometric drawing, the resultant can be calculated analytically using vector components and trigonometric relationships. This approach is particularly useful when working with precise numerical data or when graphical accuracy is limited.

4.1 Resolving Vectors

Each vector is split into horizontal (x) and vertical (y) components using trigonometry.

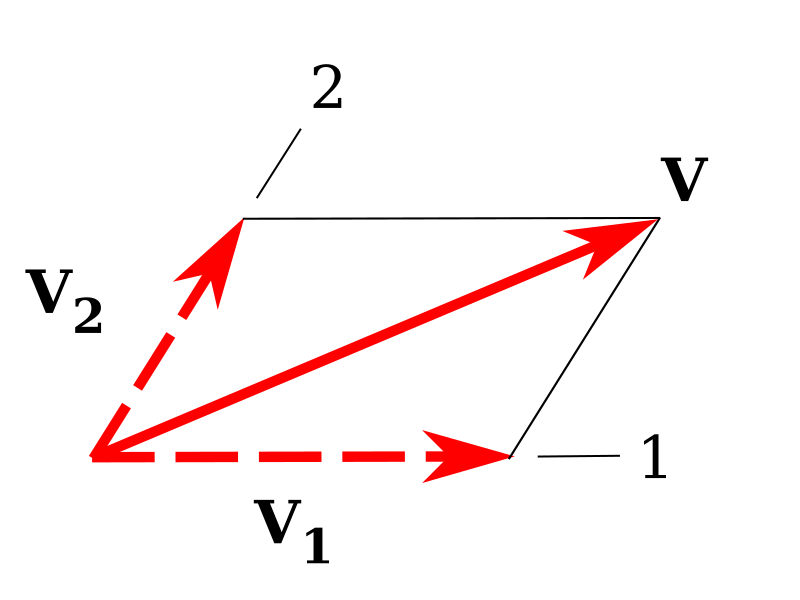
A single vector with clearly labelled rectangular components along perpendicular axes. This representation underpins the analytical method: sum components to obtain (R_x) and (R_y), then compute the resultant. (Note: the figure shows one vector’s components; applying it to two vectors requires duplicating and summing components.) Source.

The sum of these components gives the resultant’s components.

EQUATION
—-----------------------------------------------------------------
Horizontal Component (Rx) = A cosθ₁ + B cosθ₂
Vertical Component (Ry) = A sinθ₁ + B sinθ₂
Resultant Magnitude (R) = √(Rx² + Ry²)
Resultant Direction (φ) = tan⁻¹(Ry / Rx)
—-----------------------------------------------------------------

The use of trigonometric functions ensures both the magnitude and direction of the resultant can be determined mathematically without relying on scale drawings.

5. Graphical Techniques and Scale Drawings

Although analytical methods are exact, graphical methods are fundamental in visualising vector relationships. In the OCR A-Level context, students must be able to construct and interpret accurate vector diagrams.

5.1 Steps for Constructing a Scale Drawing

When using a scale drawing to find the resultant of two coplanar vectors:

• Choose an appropriate scale (e.g. 1 cm represents 10 N).

• Draw the first vector to scale, in the correct direction.

• From its tip, draw the second vector to scale at the specified angle.

• Join the tail of the first vector to the tip of the second to complete the vector triangle.

• Measure the length and angle of the resultant to determine its magnitude and direction.

5.2 Ensuring Accuracy

• Always label vectors clearly with magnitude and direction.

• Use a protractor and ruler to maintain accuracy.

• Ensure the scale is consistent throughout the diagram.

• Where precision is important, repeat the drawing with varying scales to confirm results.

This method visually reinforces the triangle law and demonstrates that vector addition is independent of the order in which vectors are combined.

6. Physical Interpretation

The concept of the resultant of two coplanar vectors underpins many physical applications. For instance:

• The net force acting on an object is the resultant of all individual forces.

• The velocity of a moving boat or aircraft combines the craft’s speed with wind or current velocity.

• The displacement of a particle moving along successive paths can be expressed as the resultant of individual displacements.

Each of these scenarios can be modelled using vector addition, ensuring that both direction and magnitude are accounted for. This emphasises that vectors cannot be treated as simple scalar quantities.

7. Importance of Correct Representation

In practical and theoretical work, representing vectors clearly is vital. Errors in direction or scale can lead to significant misinterpretations. Therefore:

• Always specify the reference direction (e.g. horizontal, north).

• Indicate the angle between vectors precisely.

• Confirm that all vectors lie in the same plane before applying the coplanar triangle method.

Attention to such details ensures that the resultant obtained accurately represents the physical reality being modelled.