Projectile motion describes the curved path followed by an object that moves through the air under the influence of gravity alone. Understanding how horizontal and vertical components operate independently is essential for analysing two-dimensional motion and predicting an object’s position at any point in time.

The Nature of Projectile Motion

A projectile is any object that is given an initial velocity and then moves freely under the influence of gravity. Once in motion, the only significant force acting on the projectile (in idealised conditions) is weight, due to gravity. Ignoring air resistance, this force acts vertically downwards and produces a constant vertical acceleration. The horizontal motion remains unaffected by gravity and continues at constant velocity.

The path traced by a projectile is known as a trajectory, and it takes the shape of a parabola. To analyse this motion accurately, it must be resolved into two separate components that can be studied independently.

Independence of Horizontal and Vertical Motion

The key principle of this subtopic is that the horizontal and vertical components of projectile motion are independent of one another. This means that:

• The horizontal velocity does not influence how quickly the projectile accelerates downward.

• The vertical acceleration (caused by gravity) does not alter the horizontal velocity.

• Both motions occur simultaneously, but the governing equations for each direction are distinct

This independence allows students to apply one-dimensional kinematic equations separately along each axis when analysing motion.

Resolving the Motion into Components

When a projectile is launched with an initial velocity v at an angle θ to the horizontal, it can be broken down into two components:

• Horizontal component (vₓ) – the velocity parallel to the ground.

• Vertical component (vᵧ) – the velocity perpendicular to the ground.

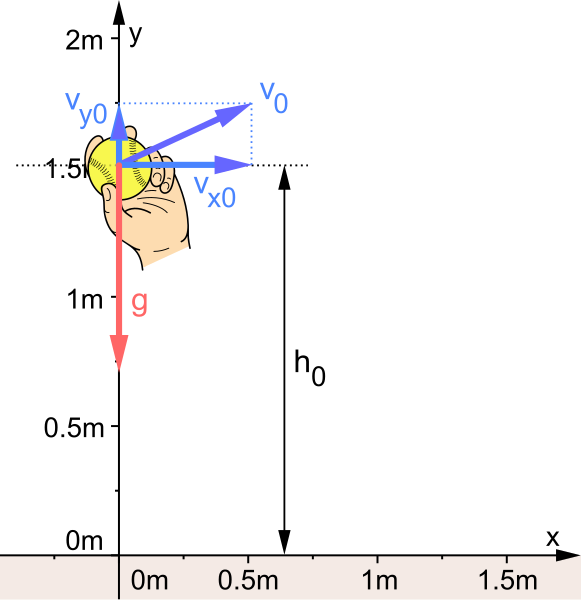
Projectile in an x–y coordinate system with the weight acting vertically. This is the standard frame for treating horizontal motion at constant velocity and vertical motion at constant acceleration. The image is intentionally minimal and does not include extra detail beyond syllabus needs. Source.

EQUATION
—-----------------------------------------------------------------
Horizontal velocity (vₓ) = v cos θ
vₓ = constant horizontal velocity (m s⁻¹)
v = initial launch velocity (m s⁻¹)
θ = launch angle (degrees or radians)
—-----------------------------------------------------------------

EQUATION
—-----------------------------------------------------------------
Vertical velocity (vᵧ) = v sin θ
vᵧ = initial vertical velocity (m s⁻¹)
v = initial launch velocity (m s⁻¹)
θ = launch angle (degrees or radians)
—-----------------------------------------------------------------

Once the velocity components are determined, they can be analysed independently using the equations of motion.

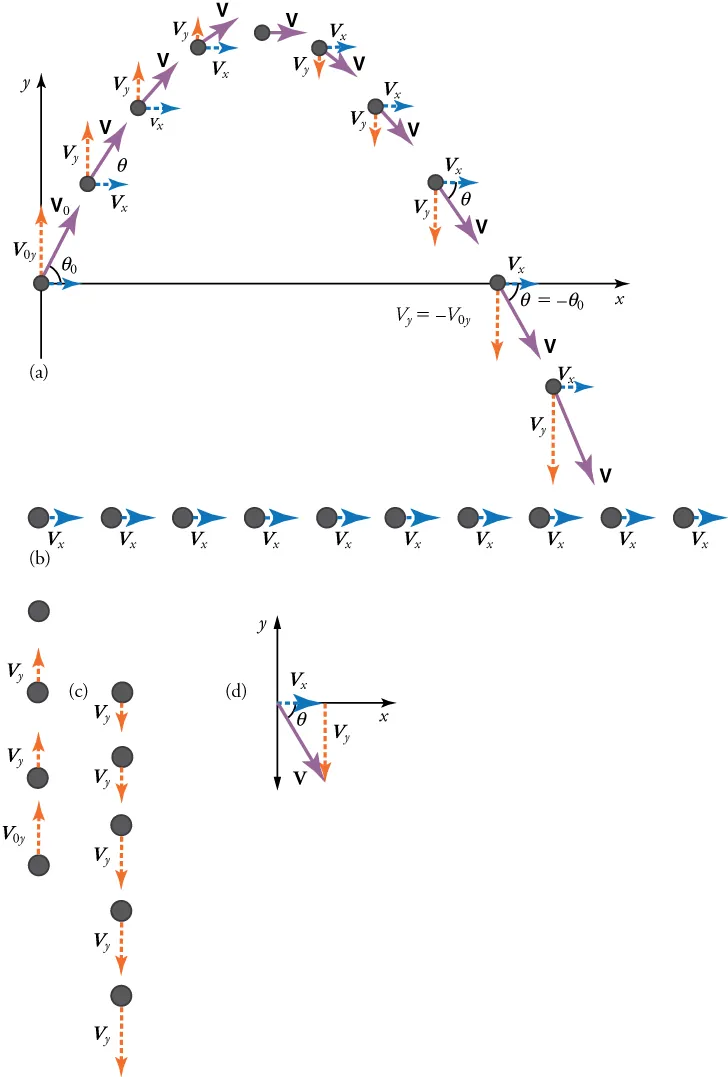
Labeled trajectory illustrating independent components of velocity: vₓ remains constant while vᵧ decreases on the way up, is zero at the apex, and increases downward. The diagram also recombines components to the resultant v. The content aligns with the model of negligible air resistance and uniform g. Source.

The horizontal motion is uniform, while the vertical motion is uniformly accelerated.

Horizontal Motion

In the absence of air resistance, no horizontal force acts on the projectile once it has been launched. Therefore, there is no horizontal acceleration, and the horizontal velocity remains constant throughout the flight.

EQUATION
—-----------------------------------------------------------------
Horizontal displacement (sₓ) = vₓ t
sₓ = horizontal displacement (m)
vₓ = constant horizontal velocity (m s⁻¹)
t = time of flight (s)
—-----------------------------------------------------------------

This equation shows that horizontal displacement depends only on the constant horizontal velocity and the time the projectile remains in the air.

Vertical Motion

The vertical component of motion behaves like any other case of motion under constant acceleration due to gravity. The acceleration is directed downwards and has a magnitude g ≈ 9.81 m s⁻² near the Earth’s surface.

EQUATION
—-----------------------------------------------------------------
Vertical displacement (sᵧ) = vᵧ t − ½ g t²
sᵧ = vertical displacement (m)
vᵧ = initial vertical velocity (m s⁻¹)
g = acceleration due to gravity (9.81 m s⁻²)
t = time elapsed (s)
—-----------------------------------------------------------------

This equation reveals how the upward velocity gradually decreases under the influence of gravity, becoming zero at the maximum height, and then increases downward as the projectile falls.

Key Features of Projectile Motion

Understanding the distinct roles of horizontal and vertical components enables accurate interpretation of a projectile’s behaviour:

• Horizontal motion: uniform, constant speed, zero acceleration.

• Vertical motion: uniformly accelerated, due to constant g.

• Time of flight: determined entirely by the vertical motion; both ascent and descent take equal times if the launch and landing heights are the same.

• Range: the total horizontal distance travelled depends on horizontal velocity and total flight time.

• Maximum height: reached when the vertical velocity momentarily becomes zero.

These features show that while the motions are independent, they are linked by time — both components share the same duration of motion.

Analysing Motion Graphically

Graphical representations can aid conceptual understanding:

• A displacement–time graph for vertical motion shows a symmetric rise and fall.

• A velocity–time graph for vertical motion is a straight line with negative gradient equal to −g.

• A horizontal displacement–time graph is a straight line with positive constant gradient.

Because the horizontal motion is uniform, the overall two-dimensional path produced by combining these independent graphs is a parabola, a classic signature of projectile motion.

Practical Interpretation and Modelling Assumptions

For OCR A-Level Physics, it is vital to remember that this independence relies on simplified modelling assumptions:

• Air resistance is negligible, meaning no horizontal deceleration.

• The acceleration due to gravity (g) is constant and uniform.

• The projectile is treated as a point mass, ignoring rotation or shape effects.

While these assumptions make analysis straightforward, they are only approximations of real-world conditions. In actual motion, air resistance and variations in g can cause noticeable deviations from ideal predictions.

Experimental Context

In a laboratory, students can explore the independence of components using projectile launchers or data-loggers to record the path of a small object such as a steel ball. By measuring the horizontal range and time of flight, it is possible to confirm that:

• The horizontal velocity remains constant.

• The vertical acceleration matches g.

Such experiments reinforce the theoretical concept that the two components act independently but occur simultaneously, combining to form the curved trajectory observed.