Projectile motion modelling simplifies complex real-world motion into an idealised framework. By assuming constant acceleration vertically and uniform velocity horizontally, students can predict and analyse trajectories mathematically and conceptually.

The Nature of Modelling in Projectile Motion

A model in physics is a simplified representation of a real system used to understand and predict physical behaviour. In projectile motion, the simplified two-dimensional model allows physicists to calculate position, velocity, and time using mathematical relationships derived from Newton’s laws. The accuracy of predictions depends on how closely real motion follows the assumptions within the model.

Modelling assumes that horizontal and vertical components of motion are independent, allowing separate analysis of each direction. In practice, this separation is only valid when external influences such as air resistance are negligible.

Core Assumptions of the Projectile Model

Negligible Air Resistance

The model assumes air resistance is negligible, meaning the projectile experiences no drag force opposing its motion.

By neglecting this force, the projectile maintains a constant horizontal velocity, as no horizontal forces act upon it after launch. Vertically, the only force considered is weight, producing a constant acceleration due to gravity. This assumption holds reasonably well for small, dense objects moving at moderate speeds, such as metal spheres in laboratory conditions.

However, in real-world contexts such as ballistics or sports, air resistance significantly alters the trajectory:

• The range is reduced because drag slows horizontal motion.

• The maximum height and time of flight are shortened.

• The path becomes less symmetrical — the descent is steeper than the ascent.

These deviations show that the ideal trajectory is parabolic, while the real trajectory is non-parabolic due to air drag.

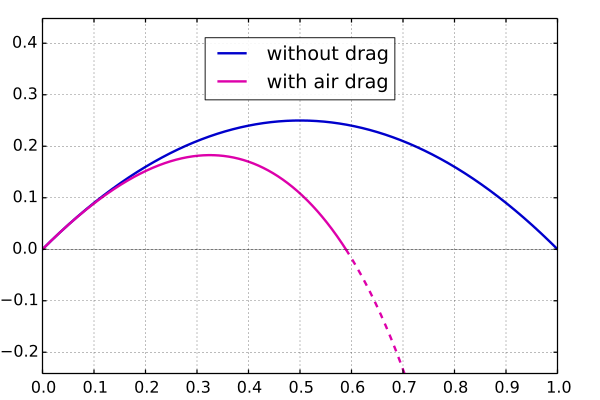
Plot showing two trajectories for equal launch conditions: the ideal parabola without drag and the shorter, steeper path with air drag. The figure highlights reduced range and asymmetry introduced by resistive forces. Extra parameters shown in the description reflect the author’s numerical model but are not required by the OCR syllabus. Source.

Uniform Gravitational Field (Constant g)

Another key assumption is that gravitational acceleration (g) is uniform — constant in both magnitude and direction throughout the projectile’s flight.

In reality, g varies slightly with altitude, latitude, and local geological conditions. For short trajectories near Earth’s surface, these variations are minimal and can be ignored. However, for long-range missiles, spacecraft launches, or motion at high altitudes, g decreases measurably with height, and the assumption of uniform gravity becomes invalid.

Under uniform g, vertical motion can be treated using the SUVAT equations for constant acceleration. These equations simplify the prediction of displacement, velocity, and time, provided the vertical acceleration remains constant.

Point Mass Approximation

The model treats the projectile as a point mass — an object with mass but no size, rotation, or surface features.

This simplification removes the complexity of analysing rotational motion, aerodynamic lift, and torque. The assumption is appropriate for small, compact projectiles such as metal spheres or pellets. In contrast, real objects like footballs, arrows, or shuttlecocks rotate, experience drag, and may even generate lift due to their shape and spin.

Ignoring size and shape also means that the centre of mass is assumed to follow the calculated trajectory exactly, even though in reality spin and air flow can shift the motion path slightly.

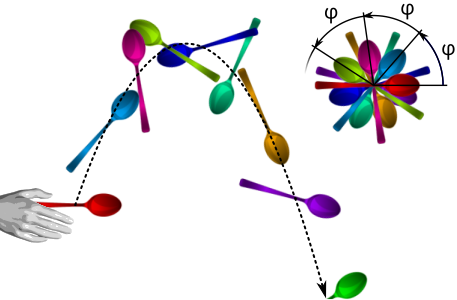
Strobe sequence of a rotating object; the marked COM travels on a smooth parabolic path while the object spins about it. This neatly justifies the point-mass approximation used in basic projectile models. The strobe lab setup is more detailed than required, but the only essential takeaway is the COM’s parabolic path. Source.

Limitations of the Model in Real Situations

Non-Uniform Air Resistance

Air resistance depends on several factors:

• Speed: Drag increases approximately with the square of velocity.

• Surface area and shape: Streamlined objects experience less resistance.

• Air density: Changes with temperature, pressure, and altitude.

Because these variables fluctuate, real projectiles often deviate significantly from ideal predictions. The model cannot account for terminal velocity, where drag balances weight, or for turbulent flow effects at high speeds.

Rotational and Magnus Effects

When a spinning object moves through air, pressure differences form around its surface, creating lift or sideways forces. This Magnus effect causes curved trajectories — for example, in a spinning football or tennis ball.

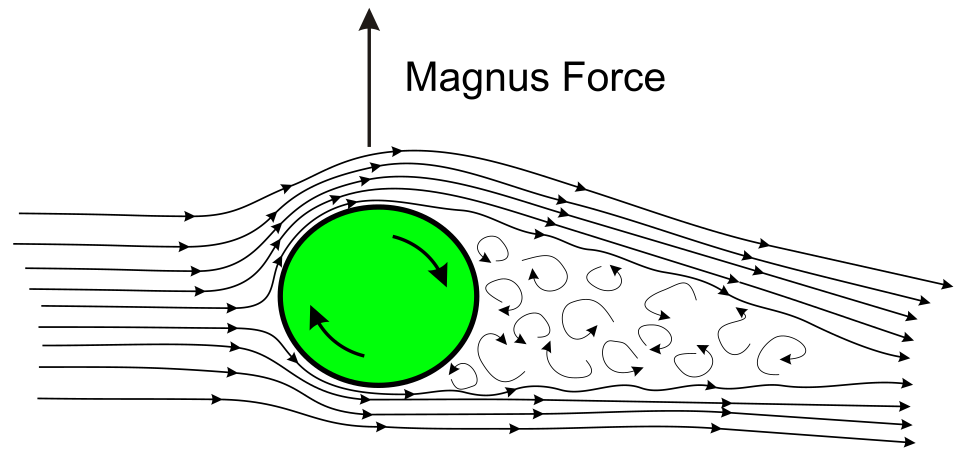
Diagram of a rotating body in airflow with deflected streamlines, pressure imbalance, and a lift force perpendicular to the flow. It explains why spin makes a projectile curve, a limitation excluded by the point-mass model. The cylinder idealisation is slightly more general than a ball but remains pedagogically appropriate. Source.

The standard projectile model, which assumes a point mass with no spin, completely omits these effects.

Atmospheric Variation and Wind

The model presumes still air with no horizontal wind. In real environments:

• Wind velocity alters the horizontal component of motion.

• Temperature gradients and air turbulence produce unpredictable deviations.
  Thus, experimental projectile motion often requires repeated trials to estimate an average path.

Large-Scale or High-Altitude Motion

For large-scale trajectories, such as artillery shells or satellites:

• Earth’s curvature becomes relevant, invalidating the assumption of a flat Earth surface.

• Gravitational acceleration decreases with distance from the Earth’s centre.

• Coriolis forces, due to Earth’s rotation, deflect motion sideways.

These effects are negligible in classroom experiments but must be included in professional applications involving long distances or extended flight times.

The Role of Assumptions in Experimental Analysis

Recognising and controlling assumptions is vital when designing experimental investigations of projectile motion. Using air tracks, light gates, or data loggers allows students to minimise unwanted influences and approach ideal conditions. However, all measurements still carry experimental uncertainty due to timing errors, surface friction, and imperfect alignment.

Students should always state the assumptions used when applying the model to ensure clarity in their analysis. Understanding both its usefulness and its limits reinforces accurate physical reasoning and the ability to evaluate whether the model’s predictions remain valid for a given situation.