OCR Specification focus:
‘Explain reaction time and thinking distance; distinguish braking distance and stopping distance for vehicles.’
Understanding how reaction time, thinking distance, and braking distance contribute to a vehicle’s stopping distance is essential for analysing motion and safety in real-world driving scenarios.
Reaction Time and Human Response in Motion
Human response to hazards involves a short delay between perceiving a danger and physically beginning to brake. This delay is called the reaction time, and it directly influences the thinking distance of a moving vehicle.
Reaction Time: The time taken for a driver to respond to a stimulus, such as noticing a hazard, before taking an action like pressing the brake pedal.
During this time, the vehicle continues to travel at its original speed, covering a certain distance before braking begins. This portion of the total stopping distance is known as the thinking distance.
Thinking Distance: The distance travelled by a vehicle between the driver perceiving a need to stop and the driver beginning to apply the brakes.
The reaction process involves sensory perception, mental processing, and muscle response. It depends on both physiological and psychological factors, and varies significantly between individuals.
Factors Affecting Reaction Time
Reaction time is not constant and can vary due to multiple influences:
Alertness and fatigue — tired drivers have slower neural response times.
Distractions — use of mobile phones, conversation, or in-car entertainment delays reaction.
Alcohol or drugs — substances impair cognitive function, significantly increasing reaction delay.
Age — older drivers may have slower reactions due to changes in nerve conduction speed.
Visibility and lighting — low visibility can extend the perception phase, effectively lengthening reaction time.
For a typical alert driver, reaction time averages around 0.7 to 1.0 seconds, although this can vary widely.
Thinking Distance and Its Relationship with Speed
Thinking distance depends directly on both reaction time and vehicle speed.
It is determined by how far the vehicle travels during the driver’s reaction period.
EQUATION
—-----------------------------------------------------------------
Thinking Distance (dₜ) = Speed (v) × Reaction Time (tᵣ)
v = velocity of the vehicle (m s⁻¹)
tᵣ = driver’s reaction time (s)
—-----------------------------------------------------------------
Because speed is a linear factor, doubling the vehicle’s speed doubles the thinking distance. For example, a car travelling at 30 m s⁻¹ covers twice as much distance in one second as a car moving at 15 m s⁻¹. This proportional relationship emphasises the significance of obeying speed limits for road safety.
Practical Considerations
Driver training aims to reduce reaction time by increasing hazard awareness.
Modern safety systems, such as collision warning sensors, assist in reducing effective reaction delay.
Environmental conditions such as rain or fog can make hazards harder to detect, indirectly lengthening the thinking distance.
Braking Distance and Vehicle Dynamics
After the brakes are applied, the vehicle travels a further distance before stopping. This is the braking distance, determined by the rate at which deceleration occurs due to braking forces acting on the vehicle.
Braking Distance: The distance a vehicle travels from the moment the brakes are applied until it comes to a complete stop.
The braking distance depends on the vehicle’s initial velocity, braking force, and road conditions. Since braking involves uniform deceleration under constant force (in ideal conditions), the relationship between distance, speed, and acceleration can be derived from the equations of motion.
EQUATION
—-----------------------------------------------------------------
Braking Distance (s) = v² / (2a)
v = initial velocity of the vehicle (m s⁻¹)
a = magnitude of deceleration due to braking (m s⁻²)
—-----------------------------------------------------------------
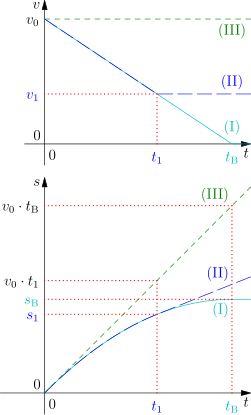
Stacked graphs show velocity vs time and displacement vs time for braking with constant deceleration. This visualises braking time and braking distance, consistent with kinematic relations. Source.
This shows that braking distance increases with the square of velocity. Therefore, doubling speed quadruples braking distance — a critical concept for safe driving analysis.
Factors Affecting Braking Distance
Several variables influence braking effectiveness:
Condition of tyres — worn or under-inflated tyres reduce grip, increasing distance.
Road surface — wet, icy, or loose surfaces decrease friction, lengthening stopping distance.
Brake condition — damaged or overheated brakes provide less force and slower deceleration.
Mass of vehicle — heavier vehicles require more force to decelerate, leading to longer braking distances.
Incline of road — braking uphill shortens distance; downhill increases it.
Vehicle safety systems such as ABS (Anti-lock Braking System) maintain traction during braking, preventing wheel lock and allowing controlled deceleration, thereby reducing effective braking distance on slippery surfaces.
Total Stopping Distance
The stopping distance is the total distance a vehicle travels from the moment a driver perceives a hazard to the point where the vehicle completely stops.
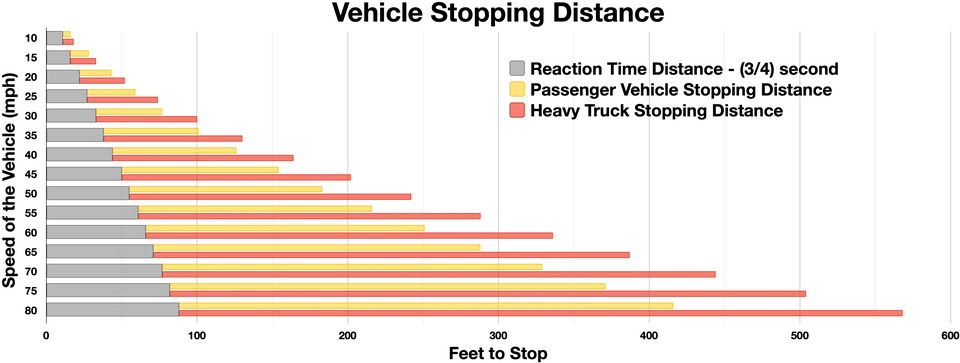
A labelled stopping-distance bar showing thinking and braking components that add to total stopping distance. Heavy-truck data are included but not required by the OCR syllabus. Source.
Stopping Distance: The total distance travelled between the driver’s perception of a hazard and the vehicle coming to a complete stop; it equals the sum of thinking and braking distances.
EQUATION
—-----------------------------------------------------------------
Stopping Distance (dₛ) = Thinking Distance (dₜ) + Braking Distance (d_b)
dₜ = distance travelled during driver’s reaction (m)
d_b = distance travelled during braking phase (m)
—-----------------------------------------------------------------
This total distance integrates human factors (reaction and perception) and mechanical factors (braking and friction). Both components must be minimised for optimal road safety.
Typical Stopping Patterns
In dry conditions with good visibility:
At 30 mph (13.4 m s⁻¹), total stopping distance ≈ 23 metres.
At 60 mph (26.8 m s⁻¹), stopping distance increases to over 70 metres.
This reflects the non-linear growth caused by the quadratic dependency of braking distance on velocity.
Physics of Friction and Energy in Braking
Braking converts kinetic energy into thermal energy through friction between brake pads and wheels. The frictional force opposes motion, creating uniform deceleration until the vehicle stops.
EQUATION
—-----------------------------------------------------------------
Work Done by Brakes (W) = Force (F) × Distance (s) = Change in Kinetic Energy
F = braking force (N)
s = braking distance (m)
—-----------------------------------------------------------------
A greater initial kinetic energy, due to higher speed, requires more work — hence a longer braking distance for a given maximum braking force. Poor friction reduces the effective force, meaning the same energy takes longer distance to dissipate.
Applied Importance in Safety and Design
Designing safe transport systems involves understanding and controlling both reaction-related and braking-related parameters:
Driver education reduces thinking distance.
Vehicle technology (e.g., automatic braking) compensates for human delay.
Road engineering improves surface friction and visibility.
Legislation sets speed limits to manage quadratic increases in braking distance.
Through analysis of these principles, the subtopic unites human physiology and physical mechanics within motion analysis, forming an essential foundation for interpreting real-world safety applications in physics.
FAQ
Reaction time refers specifically to the interval between detecting a hazard and starting a physical response (such as moving the foot to the brake).
Response time, in some contexts, includes both reaction time and the time taken for the physical action to take effect — for example, from seeing the hazard to the brakes actually engaging.
In OCR Physics, only the reaction time is considered when calculating thinking distance; mechanical delays belong to braking dynamics.
Thinking distance depends on how far the vehicle travels during a constant reaction time — a direct proportionality to speed.
Braking distance depends on the work–energy principle: kinetic energy increases with the square of speed (½mv²), so more work and distance are required to dissipate it.
Hence, doubling speed doubles thinking distance but roughly quadruples braking distance.
Systems like Automatic Emergency Braking (AEB) and Forward Collision Warning (FCW) reduce or remove the human reaction component.
AEB automatically applies brakes if the driver fails to react in time, reducing or eliminating thinking distance.
Electronic Stability Control and ABS ensure efficient braking by maintaining traction, shortening braking distance.
Although they reduce human error, drivers must still account for system lag and sensor limitations.
When travelling uphill, part of the vehicle’s weight acts against motion, effectively increasing deceleration and reducing braking distance.
When travelling downhill, gravity aids motion, reducing the net deceleration and increasing braking distance.
In calculations, the acceleration term becomes a ± g sinθ, depending on slope direction. This factor can significantly change stopping distance on steep roads.
Perception time — identifying and interpreting a hazard — often dominates overall reaction time.
It involves:
Detection: noticing an event (e.g., brake lights ahead).
Recognition: understanding it as a hazard.
Decision: choosing to act (e.g., brake).
Fatigue, poor lighting, and distraction extend perception time, meaning the driver begins braking later, increasing thinking distance even if braking performance is unchanged.
Practice Questions
Question 1 (2 marks)
A driver is travelling at 20 m s⁻¹ when they notice an obstacle. Their reaction time is 0.8 s.
(a) Define thinking distance.
(b) Calculate the thinking distance for the driver.
Mark Scheme for Question 1
(a) Definition (1 mark)
Thinking distance: the distance a vehicle travels during the driver’s reaction time, before the brakes are applied.
(b) Calculation (1 mark)
Thinking distance = speed × reaction time
= 20 × 0.8 = 16 m.
Question 2 (5 marks)
A car is moving along a dry road at 25 m s⁻¹. The driver’s reaction time is 0.9 s, and the car decelerates uniformly at 6.0 m s⁻² when the brakes are applied.
(a) Calculate the total stopping distance for the car.
(b) Explain why the stopping distance would be greater on an icy road, even if the driver’s reaction time remained the same.
Mark Scheme for Question 2
(a) Calculation (3 marks total)
Step 1: Thinking distance = speed × reaction time = 25 × 0.9 = 22.5 m (1 mark)
Step 2: Braking distance = v² / (2a) = (25²) / (2 × 6.0) = 625 / 12 = 52 m (approx.) (1 mark)
Step 3: Total stopping distance = 22.5 + 52 = 74.5 m (accept 74–75 m) (1 mark)
(b) Explanation (2 marks total)
On an icy road, the frictional force between tyres and road is greatly reduced (1 mark).
This results in a smaller deceleration, so the car takes longer to stop and travels a greater braking distance (1 mark).

