Newton’s Second Law and the Newton

Understanding how forces produce motion lies at the heart of classical mechanics. Newton’s Second Law of Motion quantifies the relationship between force, mass, and acceleration, forming a cornerstone of A-Level Physics study.

Newton’s Second Law of Motion

Historical Context and Concept

Sir Isaac Newton’s Second Law describes how an object’s motion changes when a resultant force acts upon it. It bridges the link between the cause of motion (force) and the effect (acceleration). The law is essential for analysing motion in one or more dimensions and provides the mathematical foundation for dynamics.

Statement of the Law

Newton’s Second Law states that the rate of change of momentum of an object is directly proportional to the resultant force acting on it, and occurs in the direction of that force.

This description emphasises that forces cause changes in motion, not motion itself, highlighting the dynamic relationship between applied forces and the acceleration they produce.

Relating Force, Mass, and Acceleration

EQUATION
—-----------------------------------------------------------------
Newton’s Second Law (Force) = F = ma
F = Resultant force acting on the object (newton, N)
m = Mass of the object (kilogram, kg)
a = Acceleration of the object (metres per second squared, m s⁻²)
—-----------------------------------------------------------------

The equation F = ma applies when the mass remains constant. It provides a quantitative relationship: the greater the resultant force on an object, the greater its acceleration, and vice versa. Similarly, for the same force, an object with larger mass experiences smaller acceleration.

This relationship can be applied in one or more dimensions using vector notation, meaning both direction and magnitude must be considered.

The Newton as the Unit of Force

Definition and Use

The newton (N) is the SI unit of force. It standardises the measurement of force across physical systems and ensures consistency across equations and experimental data.

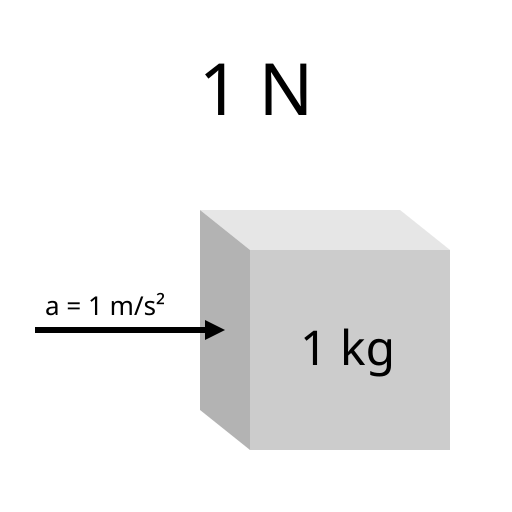
One newton is defined as the force required to accelerate a mass of 1 kg at 1 m s⁻². The cube represents the mass and the arrow the acceleration vector, linking directly to F = ma. Source.

Hence,
1 N = 1 kg m s⁻²

This definition arises directly from Newton’s Second Law and underpins all quantitative descriptions of force in mechanics.

Understanding Resultant Force

Multiple Forces and Vector Addition

Objects rarely experience a single force. Often, several forces act simultaneously—gravitational, normal contact, tension, friction, or applied forces. The resultant force is the vector sum of all individual forces acting on an object.

A free-body diagram displays all external forces acting on a body as vectors. Here, weight, normal contact, applied force and friction are shown so that their vector sum (the net force) can be determined. Once the net force is known, F = ma gives the acceleration in magnitude and direction. Source.

When the resultant force is zero, an object either remains at rest or moves at constant velocity, consistent with Newton’s First Law. When the resultant force is non-zero, acceleration occurs according to Newton’s Second Law.

To determine the resultant force:

• Represent all forces as vectors with direction and magnitude.

• Use vector addition (parallelogram or component methods) to find the single resultant.

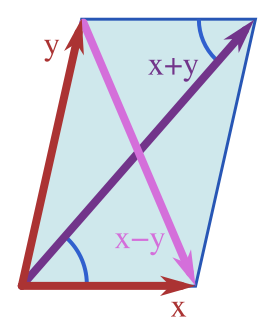
Two concurrent forces are represented as adjacent sides of a parallelogram; the diagonal gives the resultant. This geometric construction embodies vector addition for forces. Once the resultant is obtained, Newton’s Second Law links it to the object’s acceleration. Source.

• Apply F = ma to predict the resulting acceleration.

Acceleration and Direction of Motion

Acceleration is a vector quantity, meaning it possesses both magnitude and direction. It always acts in the same direction as the resultant force. However, velocity and acceleration are not always aligned. For instance:

• If the force opposes motion, acceleration acts against velocity, causing deceleration.

• If the force acts perpendicular to velocity, as in circular motion, the object changes direction without changing speed.

This directional dependency ensures that Newton’s Second Law fully explains linear and curved motion under constant or varying forces.

Relationship with Momentum

Newton’s original formulation of his Second Law was expressed in terms of momentum (p), defined as the product of mass and velocity. This version emphasises that forces cause changes in momentum, not just acceleration.

The law can therefore be expressed as:

EQUATION
—-----------------------------------------------------------------
Force (F) = Δp / Δt
F = Resultant force acting on the object (N)
Δp = Change in momentum (kg m s⁻¹)
Δt = Time interval (s)
—-----------------------------------------------------------------

When the mass remains constant, Δp = mΔv, leading back to F = ma. This formulation is especially useful in systems where the mass changes, such as rocket propulsion, where expelling exhaust gases changes momentum.

Applying Newton’s Second Law in Practice

Identifying Forces

When applying F = ma in practical contexts:

• Identify all forces acting on the object.

• Determine whether the motion is linear or two-dimensional.

• Resolve forces into components when necessary (for instance, along horizontal and vertical axes).

• Calculate the resultant force.

• Use F = ma to find the acceleration or force required.

Common examples include:

• A car accelerating under an engine’s thrust while opposed by resistive forces.

• An object sliding down an inclined plane, where gravity and friction act simultaneously.

• A projectile where gravitational force is the only significant force acting after launch.

Each situation involves balancing or combining forces and applying Newton’s Second Law to determine the object’s motion.

The Role of Mass and Inertia

Mass represents an object’s inertia, or resistance to changes in motion. A larger mass requires a greater force to produce the same acceleration. This principle is fundamental to understanding why heavier objects are harder to start or stop moving.

By linking mass and acceleration through the Second Law, physics provides a consistent framework for predicting how different bodies respond to applied forces.

Consistent Use of Units and Measurement

For successful application of Newton’s Second Law, unit consistency is crucial:

• Force must be in newtons (N).

• Mass must be in kilograms (kg).

• Acceleration must be in metres per second squared (m s⁻²).

Any deviation in units leads to incorrect results. Always convert quantities before substituting them into the equation.

Furthermore, when analysing complex problems, remember:

• Vectors must include both magnitude and direction.

• Acceleration and resultant force share the same direction.

• If the resultant force is zero, acceleration is zero, confirming equilibrium of forces.

The Significance of Newton’s Second Law

Newton’s Second Law forms the foundation for almost all of mechanics. It explains how and why motion changes under applied forces and provides the quantitative tools for predicting future motion. Its definition of the newton gives physics a coherent, universal measure of force, vital for accurate communication and consistent calculation across all physical sciences.