OCR Specification focus:
‘Calculate weight using W = mg; distinguish mass and weight in problems and diagrams.’
Understanding weight and gravitational force is fundamental to analysing motion and forces in physics. This topic explores how mass interacts with gravity to produce measurable forces and how these differ conceptually.
Weight and Gravitational Force
Weight is the force due to gravity acting on a mass. It links an object’s mass to the strength of the gravitational field in which it is located.
EQUATION
—-----------------------------------------------------------------
Weight Equation (W) = m g
W = Weight, measured in newtons (N)
m = Mass, measured in kilograms (kg)
g = Gravitational field strength, measured in newtons per kilogram (N kg⁻¹)
—-----------------------------------------------------------------
The equation shows that an object’s weight depends directly on both its mass and the gravitational field strength. On Earth, g ≈ 9.81 N kg⁻¹, though it varies slightly with altitude and location.
Distinguishing Between Mass and Weight
These two terms are often confused, but in physics they have distinct meanings:
Mass: The amount of matter in an object; a scalar quantity that remains constant regardless of location.
Weight: The force exerted on a mass by a gravitational field; a vector quantity that acts towards the centre of the attracting body.
Because mass is a measure of matter, it does not change whether the object is on Earth, the Moon, or in space. Weight, however, changes because g differs in each environment. For example, an object’s weight on the Moon is roughly one-sixth of its weight on Earth due to the weaker gravitational field.
The Nature of Gravitational Force
All masses exert a gravitational attraction on one another. For everyday objects, this force is negligible, but between a planet and an object it is significant. The gravitational field around Earth can be visualised as a region where a mass experiences an attractive force towards the planet’s centre.
A labelled diagram of Earth with gravitational field lines directed toward the centre. It reinforces that weight is the force a mass experiences in a gravitational field, acting radially inward. The equipotential curves shown are a helpful extra not required by the syllabus, but they clarify how field strength relates to position. Source.
The gravitational force always acts vertically downwards near Earth’s surface.
It is responsible for keeping projectiles following curved paths and for maintaining planetary orbits.
The direction of weight is essential in constructing free-body diagrams, where weight is shown as an arrow pointing down from the object’s centre of mass.
Representing Weight in Diagrams
When analysing forces acting on an object, it is standard to include the weight as one of the main vectors:
For objects at rest on a surface, the weight (W) acts downwards and is balanced by the normal contact force (N) acting upwards.
For objects hanging from a string, weight acts down while tension (T) acts upwards through the string.
For falling objects, weight is the unbalanced force when air resistance (drag) is negligible.
Diagrams must always label weight clearly as W = mg, indicating its direction and acting point (typically through the centre of mass).
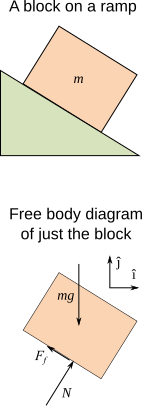
A free-body diagram of a block on an inclined plane with vectors for weight (mg), normal contact force, and friction. Use it to emphasise the direction and labelling of weight in diagrams. Note: the incline and frictional components exceed the syllabus requirement for this subsubtopic but do not add unnecessary clutter. Source.
Variation of Weight with Gravitational Field Strength
The gravitational field strength g depends on the mass of the celestial body and its radius. It can be calculated using Newton’s law of gravitation, though OCR students only need to apply the simpler proportional reasoning:
Larger planets or those with higher mass have greater g, hence greater weight for the same mass.
As altitude increases, g decreases slightly because the distance from the planet’s centre increases.
On smaller celestial bodies, such as the Moon or Mars, g is weaker, so the same object weighs less.
EQUATION
—-----------------------------------------------------------------
Proportional Relationship: W ∝ g
Meaning: As gravitational field strength increases, weight increases proportionally for the same mass.
—-----------------------------------------------------------------
This principle explains why astronauts feel almost weightless on the Moon, even though their mass remains unchanged.
Mass and Weight in Practical Contexts
When interpreting experimental data or physical situations:
Mass is measured using a balance, which compares the object’s matter to a reference mass.
Weight is measured using a newtonmeter (spring balance), which measures the force due to gravity directly.
Instruments calibrated on Earth assume g = 9.81 N kg⁻¹; if used elsewhere, corrections must be made.
In problem-solving and diagrams, ensure the correct distinction:
Use mass (m) in equations involving inertia or kinematics.
Use weight (W) when dealing with forces or equilibrium.
Effects of Weight on Motion
A constant resultant force produces acceleration according to Newton’s second law, and when only gravity acts, this acceleration is free fall. Thus:
EQUATION
—-----------------------------------------------------------------
Resultant Force (F) = m a
a = Acceleration, measured in metres per second squared (m s⁻²)
—-----------------------------------------------------------------
In free fall near Earth, a = g, showing that all objects accelerate equally under gravity, neglecting air resistance. This equality between gravitational and inertial mass was a key finding in classical physics and remains a cornerstone of modern gravitational theory.
Conceptual Understanding of Weightlessness
An object is weightless if it experiences no contact force supporting it, even though gravity may still act. For instance:
Astronauts in orbit are in continuous free fall towards Earth, but because they fall at the same rate as their spacecraft, they experience apparent weightlessness.

A NASA photograph of Expedition 67 crew members with objects floating in the cabin. The scene illustrates apparent weightlessness: gravity is still present, but supporting contact forces are absent during free fall. The image includes mission context not required by the syllabus but vividly conveys the concept. Source.
True absence of weight occurs only far from any significant gravitational field, where g ≈ 0.
This distinction reinforces that weightlessness does not mean no gravity, but rather no reaction force opposing gravity.
Summary Points for Application
To apply this subtopic in physics problems and diagrams, remember:
Use W = mg to calculate weight from known mass and gravitational field strength.
Clearly distinguish mass and weight: mass is scalar and constant; weight is vector and variable.
Always label weight correctly in free-body diagrams, acting vertically through the centre of mass.
Recognise that g varies with location, so the same object can have different weights on different planets or altitudes.
Understand that weightlessness is the result of free fall or negligible gravitational fields, not the absence of mass.
FAQ
The object’s mass remains unchanged because it represents the amount of matter present, which is independent of location.
However, the weight decreases slightly because gravitational field strength, g, becomes weaker with distance from Earth’s centre. Although the change is small at low orbital heights, it is measurable.
In orbit, the object is in free fall, so it appears weightless — there is no contact force acting on it even though gravity still exerts a force.
The value of g is not perfectly constant. It varies slightly due to:
Altitude: g decreases with height above sea level.
Latitude: the Earth’s rotation causes a small outward centripetal effect, reducing g at the equator compared to the poles.
Local density variations: mountain ranges or mineral deposits can alter the local gravitational field.
These variations are small, typically less than 0.05 N kg⁻¹, but are important in precision measurements and satellite calibration.
Weightlessness can be simulated in several ways:
Parabolic flight: an aircraft follows a steep parabolic trajectory. During the free-fall portion, everything inside experiences microgravity for about 20 seconds.
Drop towers: experiments are dropped from height in evacuated shafts, creating a few seconds of apparent weightlessness.
Neutral buoyancy tanks: astronauts train underwater, where buoyancy counteracts weight to mimic the experience of reduced gravity.
Each method reproduces the effects of apparent weightlessness for brief periods, aiding research and astronaut preparation.
True weightlessness occurs only where there is no significant gravitational field — far from massive bodies. In such conditions, g is effectively zero, and objects experience no gravitational force.
Apparent weightlessness happens when gravity acts but there is no reaction or support force, such as in orbit. Both astronauts and spacecraft fall together at the same rate, removing any sensation of weight even though gravity still acts on them.
A gravimeter measures variations in gravitational acceleration (g) rather than weight directly.
Most gravimeters work by detecting changes in the position of a suspended mass or a vibrating spring system when gravity acts.
If g increases, the mass is pulled slightly further down or vibrates at a different frequency.
The change is measured electronically and converted to a precise value of g.
Such instruments are crucial for geophysical surveys, mineral exploration, and verifying local values of gravitational field strength used in physics experiments.
Practice Questions
Question 1 – (2 marks)
A student is standing on the surface of the Moon where the gravitational field strength is 1.6 N kg⁻¹. The student’s mass is 70 kg.
(a) Calculate the student’s weight on the Moon.
(b) Explain why the student’s mass is the same on the Moon as on Earth.
Mark scheme:
(a) Weight = m × g = 70 × 1.6 = 112 N (1 mark for correct substitution, 1 mark for correct answer and unit).
(b) Mass is a measure of the amount of matter in the body and does not depend on location or gravitational field strength. (1 mark)
Question 2 – (5 marks)
A spacecraft is orbiting Earth. The astronauts inside experience apparent weightlessness even though gravity still acts on them.
(a) Explain what is meant by apparent weightlessness.
(b) Describe why the astronauts experience this condition while orbiting Earth.
(c) A 75 kg astronaut on Earth has a weight of approximately 735 N.
(i) Explain why their weight would be smaller when orbiting 400 km above Earth’s surface.
(ii) Suggest why the astronaut’s mass remains the same.
Mark scheme:
(a) Apparent weightlessness means no contact or support force acts on the astronauts even though gravity still pulls them towards Earth. (1 mark)
(b) The spacecraft and astronauts are in continuous free fall towards Earth; they fall at the same rate so there is no reaction force on the astronauts. (2 marks)
(c)(i) Gravitational field strength decreases with distance from Earth’s centre; therefore weight (W = mg) is smaller in orbit. (1 mark)
(c)(ii) Mass is the amount of matter and does not depend on location or gravitational field strength. (1 mark)

