When a constant resultant force acts on an object, it produces uniform acceleration, creating predictable linear or projectile motion. Understanding this link between force and motion is central to dynamics.

The Nature of a Constant Resultant Force

A resultant force is the single net force obtained when all individual forces acting on an object are combined vectorially. If this resultant remains constant in both magnitude and direction, the object experiences a constant acceleration.

The relationship between force and motion stems directly from Newton’s Second Law of Motion, which defines how forces influence acceleration and momentum.

Newton’s Second Law and Its Implications

EQUATION
—-----------------------------------------------------------------
Newton’s Second Law (Force) = F = ma
F = resultant (net) force acting on the object, measured in newtons (N)
m = mass of the object, measured in kilograms (kg)
a = acceleration of the object, measured in metres per second squared (m s⁻²)
—-----------------------------------------------------------------

This equation shows that for a constant mass, a constant resultant force yields a constant acceleration. If the force doubles, acceleration doubles proportionally.

A constant acceleration implies that the object’s velocity changes linearly with time, producing uniform motion in one or more dimensions depending on the direction of the applied force.

One-Dimensional Motion under Constant Resultant Force

In one-dimensional motion, the force, acceleration, and velocity all act along the same line. The motion can be described using kinematic equations, derived from constant acceleration relationships.

EQUATION
—-----------------------------------------------------------------
Equations of Motion under Constant Acceleration
v = u + at
s = ut + ½at²
v² = u² + 2as
v = final velocity (m s⁻¹)
u = initial velocity (m s⁻¹)
a = acceleration (m s⁻²)
t = time (s)
s = displacement (m)
—-----------------------------------------------------------------

These equations describe how displacement, velocity, and time interrelate when the resultant force (and therefore acceleration) remains constant.

For example:

• If the resultant force acts in the same direction as motion, the object accelerates.

• If it acts opposite to the direction of motion, the object decelerates (negative acceleration).

Because the acceleration is constant, the velocity–time graph is a straight line and the displacement–time graph forms a parabola.

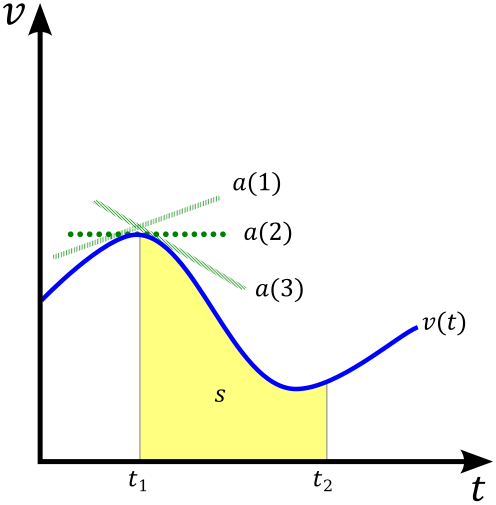
Velocity–time graph for uniform acceleration: the straight-line slope equals acceleration, while the area under the line gives displacement. This directly follows from F = ma when the resultant force is constant. The diagram focuses on essentials without extraneous annotations. Source.

Two-Dimensional Motion and Vector Methods

When a constant resultant force acts in two dimensions, motion must be treated as a vector quantity. Each component of motion is analysed separately along perpendicular axes, usually horizontal (x) and vertical (y).

Resolving Forces and Acceleration Components

The resultant force can be resolved into components using trigonometric functions:

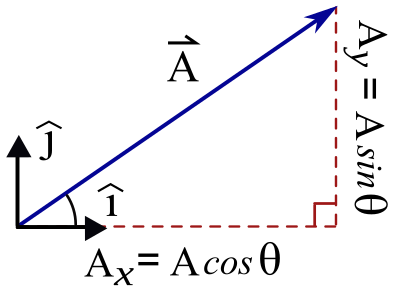
A vector resolved into orthogonal components along x and y, highlighting the method used to analyse motion under a constant resultant force. Treating components independently enables straightforward use of F = ma in each direction. The inclusion of i and j unit vectors reflects standard notation and may exceed the minimal requirement slightly. Source.

• Fₓ = F cos θ (horizontal component)

• Fᵧ = F sin θ (vertical component)

Since F = ma, the acceleration components can also be expressed as:

• aₓ = Fₓ / m

• aᵧ = Fᵧ / m

Both accelerations are constant if the resultant force and mass remain constant. These independent accelerations govern motion in each direction, and combining them produces a parabolic trajectory when both components are non-zero.

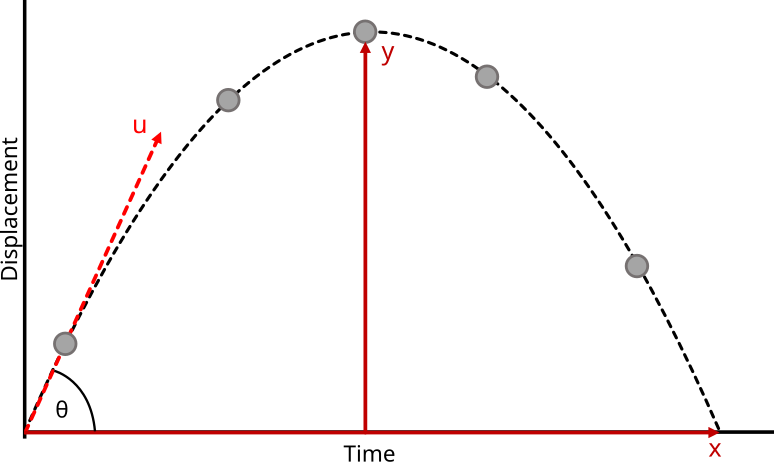
Projectile motion under a constant downward force shows uniform vertical acceleration and constant horizontal velocity, producing a parabolic path. The diagram labels u, θ, range, and maximum height to emphasise vector components and resulting motion. Extra labels (range/height) are included for clarity but are not strictly required by the specification. Source.

Vector Representation of Motion

EQUATION
—-----------------------------------------------------------------
Resultant Force as a Vector
F = m a
F = resultant force vector (N)
m = mass (kg)
a = acceleration vector (m s⁻²)
—-----------------------------------------------------------------

This vector form emphasises that acceleration shares the same direction as the resultant force. The magnitude of F determines how rapidly velocity changes, while the direction of F dictates the line along which this change occurs.

Relationship between Force, Velocity, and Displacement

Under constant resultant force:

• Acceleration is constant.

• Velocity changes linearly with time.

• Displacement changes quadratically with time.

These relationships mean that an object’s motion can be fully predicted if the initial conditions and applied force are known.

Key relationships:

• The slope of a velocity–time graph equals acceleration.

• The area under a velocity–time graph gives displacement.

• The slope of a displacement–time graph represents velocity.

Interpreting Graphs of Motion

In physics analysis, motion graphs visually reveal how a constant resultant force affects dynamics:

• A straight-line velocity–time graph indicates uniform acceleration due to a constant force.

• A parabolic displacement–time graph results from the uniform change in velocity.

• A flat line on an acceleration–time graph signifies constant acceleration, confirming constant force.

If the resultant force were to change, these graphs would show curvature or slope variation, indicating non-uniform acceleration.

Example Physical Scenarios (Conceptual)

Although detailed examples are excluded, common contexts include:

• A trolley pulled by a constant horizontal force on a frictionless track.

• A spacecraft accelerating in deep space under constant engine thrust.

• A ball projected in a uniform gravitational field, where the constant force of gravity creates a uniform downward acceleration.

Each demonstrates the same core physics: a constant resultant force produces constant acceleration, leading to motion that can be predicted using vector and kinematic analysis.

Momentum and Constant Resultant Force

When a constant resultant force acts, momentum changes uniformly over time.

EQUATION
—-----------------------------------------------------------------
Impulse and Momentum Relationship
F Δt = Δp
F = constant resultant force (N)
Δt = time interval (s)
Δp = change in momentum (kg m s⁻¹)
—-----------------------------------------------------------------

This reinforces that constant force leads to a constant rate of change of momentum. The longer the force acts, the greater the change in velocity.

Summary of Conceptual Connections

• Constant resultant force → constant acceleration

• Constant acceleration → uniform change in velocity

• Uniform change in velocity → predictable displacement and trajectory

• Vector analysis ensures motion in multiple dimensions can be decomposed into independent, orthogonal components for accurate calculation.