OCR Specification focus:
‘Outline practical techniques for measuring density, pressure and upthrust with attention to uncertainty.’
Experimental approaches to fluids and pressure are essential in developing understanding of density, pressure, and upthrust. Students must master accurate measurements, data analysis, and uncertainty evaluation.
Measuring Density
Determining the density of materials enables comparison between solids, liquids, and gases. For precise results, careful measurements of mass and volume are crucial, using suitable apparatus and accounting for uncertainty in both quantities.
Determining Density of Regular Solids
Regular solids (such as cubes or cylinders) can be measured using standard geometrical formulas once the dimensions are obtained accurately.
EQUATION
—-----------------------------------------------------------------
Density (ρ) = mass ÷ volume
ρ = density (kg m⁻³)
mass = amount of matter in the object (kg)
volume = space occupied by the object (m³)
—-----------------------------------------------------------------
For a rectangular block, a micrometer screw gauge or vernier caliper can measure dimensions to high precision. Each measurement should be repeated and averaged to reduce random uncertainty. The balance used for mass measurement should be tared before use, and its precision noted.
When calculating density, combine percentage uncertainties from mass and volume to find the total uncertainty in ρ.
Determining Density of Irregular Solids
For irregular solids, the displacement method provides a practical approach:
Fill a eureka can (displacement vessel) with water up to the spout.
Immerse the object completely; collect displaced water in a measuring cylinder.
Record the volume of displaced water as the object’s volume.
Weigh the object separately using a balance.
This method assumes no air bubbles and that the object is fully submerged. Temperature stability is important since water density changes with temperature.
Determining Density of Liquids
To determine the density of a liquid:
Measure the mass of an empty measuring cylinder.
Add a known volume of liquid and remeasure mass.
The difference gives the liquid’s mass; the volume is read directly.
Ensure eye-level reading of the meniscus to avoid parallax error. For higher accuracy, repeat the process and average multiple readings.
Determining Density of Gases
Gas density measurements require knowledge of both mass and volume of the gas. For example, a known volume of gas may be collected in a gas syringe and weighed indirectly by measuring the change in mass of the containing vessel before and after release. Control of pressure and temperature is vital because gases are highly compressible and sensitive to environmental conditions.
Measuring Pressure in Solids, Liquids, and Gases
Pressure measurements allow quantification of the force per unit area exerted by or on a surface. Different experimental techniques are required for solids, liquids, and gases.
EQUATION
—-----------------------------------------------------------------
Pressure (p) = force ÷ area
p = pressure (Pa)
force = perpendicular force applied (N)
area = surface area over which the force acts (m²)
—-----------------------------------------------------------------
Measuring Pressure in Solids
For solids, pressure can be explored by:
Using weights on a known area of contact (e.g. a wooden block).
Measuring the force (weight) using W = mg, and dividing by the area in contact.
Observing how changing area affects pressure at constant force, demonstrating the inverse relationship.
Uncertainties arise from the precision of area measurements and the calibration of the balance used for mass.
Measuring Pressure in Liquids
Hydrostatic pressure experiments use the relationship between depth, density, and gravitational field strength.
EQUATION
—-----------------------------------------------------------------
Hydrostatic Pressure (p) = ρgh
ρ = density of the liquid (kg m⁻³)
g = gravitational field strength (9.81 m s⁻²)
h = depth below the liquid surface (m)
—-----------------------------------------------------------------
A manometer or U-tube apparatus filled with fluid can demonstrate pressure differences with depth.
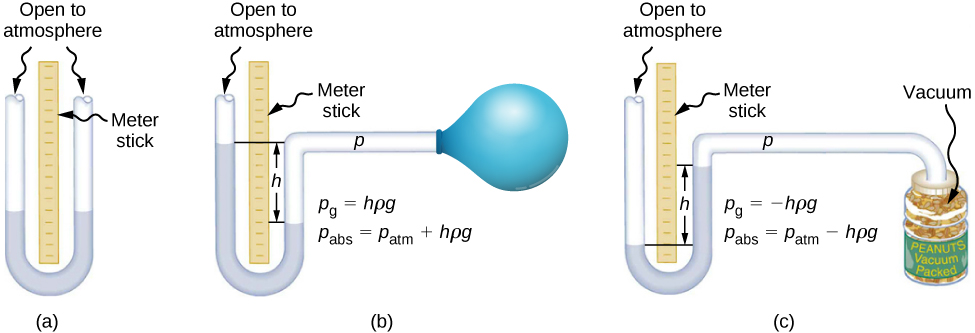
Schematic of an open-tube and connected manometer showing how a height difference h in the columns corresponds to a pressure difference p = ρgh. The diagram highlights positive and negative gauge pressure cases and reinforces that equal depths in the same fluid have equal pressure. It includes extra examples (balloon/jar) illustrating gauge vs atmospheric pressure, which are useful context but not required by the syllabus. Source.
Alternatively, inserting a pressure sensor or Pascal’s apparatus at different depths in water illustrates the linear increase of pressure with depth.
Students should account for systematic uncertainties, such as calibration errors or parallax when reading fluid levels. Ensure consistent alignment of the measuring device relative to the liquid surface.
Measuring Pressure in Gases
Gas pressure can be measured with:
Manometers, which compare gas pressure to atmospheric pressure.
Pressure sensors connected to data loggers, allowing continuous digital readings.
Bourdon gauges, which provide mechanical indication of pressure.
Temperature control is crucial; as gas temperature rises, molecular motion increases and pressure readings change. Calibration of pressure sensors should be checked before experiments.
Measuring Upthrust and Archimedes’ Principle
Upthrust arises due to pressure differences in fluids acting on immersed objects. According to Archimedes’ principle, the upthrust on an object equals the weight of the displaced fluid.
EQUATION
—-----------------------------------------------------------------
Upthrust (U) = weight of displaced fluid = ρ g V
ρ = density of the fluid (kg m⁻³)
g = gravitational field strength (9.81 m s⁻²)
V = volume of displaced fluid (m³)
—-----------------------------------------------------------------
Experimental Determination of Upthrust
To measure upthrust:
Suspend an object from a newton meter and record its weight in air.
Submerge it fully in water and record the apparent weight.
The difference between the two readings gives the upthrust.
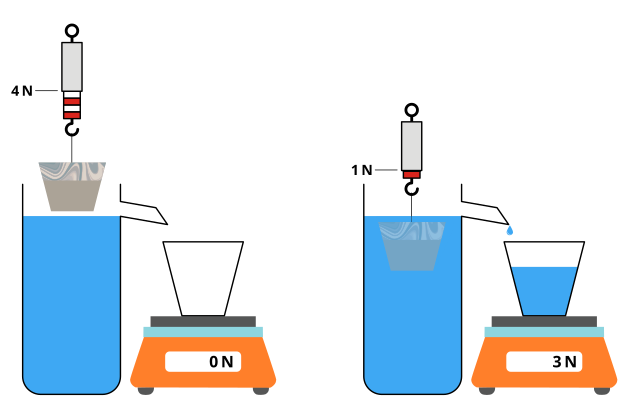
Diagram of the standard upthrust experiment: an object suspended from a spring balance is partially or fully submerged in water, reducing its apparent weight by the buoyant force. The setup allows direct comparison of readings in air and in water to verify that upthrust equals the weight of displaced fluid. The figure is schematic and does not show numerical data, which keeps it focused on apparatus and principle as required. Source.
Measure the volume of water displaced to verify Archimedes’ principle quantitatively.
Repeat readings to check for consistency and calculate the mean upthrust. Avoid errors from water adhesion or incomplete submersion. Ensure the object is not touching the sides or bottom of the vessel.
Managing Experimental Uncertainty
Understanding uncertainty is vital for all experimental work:
Random uncertainties arise from unpredictable variations; reduce them by repeating measurements and averaging.
Systematic uncertainties stem from instrument calibration or procedural bias; identify and minimise them through equipment checks and consistent methods.
Always express final results with an appropriate percentage uncertainty and quote instrument resolution (e.g. ±0.01 g for a digital balance).
Record all data with correct significant figures reflecting measurement precision. Where appropriate, present results graphically to visualise relationships and assess linearity.
Practical Considerations
Ensure apparatus is clean and dry before measuring liquids or gases.
Avoid air bubbles when immersing objects or filling manometers.
Maintain constant temperature for consistent density and pressure readings.
Document all readings carefully with units and note any anomalies for discussion.
Through precise, repeatable measurements and sound handling of uncertainty, experimental approaches to fluids and pressure reveal the quantitative relationships that underpin fluid behaviour in physics.
FAQ
The largest source of uncertainty usually comes from measuring the volume of displaced liquid, particularly due to meniscus reading errors and air bubbles adhering to the object.
To minimise this:
Ensure the eureka can is filled exactly to the spout before immersion.
Immerse the object slowly to prevent splashing or partial displacement.
Read the measuring cylinder at eye level and ensure the surface of the liquid is stable before recording.
Repeating measurements and averaging can further reduce random uncertainty.
Temperature affects both density and viscosity of fluids.
If a liquid’s temperature rises:
Its density decreases, leading to lower measured pressure or upthrust values.
Its viscosity decreases, making displacement and flow measurements inconsistent.
To ensure reliable results:
Conduct experiments in a temperature-stable environment.
Record the temperature of the fluid so that corrections can be made if necessary.
Even small variations can cause significant percentage errors in precision experiments.
Pressure sensors provide digital readings with high sensitivity and can be linked to data loggers for continuous monitoring.
Advantages include:
Reduced parallax error since readings are numerical, not visual.
Ability to measure dynamic pressure changes in real time.
Easier data analysis, including graphing and error estimation.
However, they require careful calibration against a known standard, as electronic drift or sensor lag can introduce systematic errors.
As an object enters a liquid, small turbulent currents and air bubbles can form, temporarily altering the effective upthrust.
This fluctuation occurs because:
The liquid needs time to settle around the object, establishing stable pressure distribution.
Any trapped air reduces the displaced liquid volume and thus the calculated upthrust.
Waiting a few seconds before taking the reading ensures the buoyant force stabilises, giving a more accurate result.
Systematic errors can arise from zero errors on the newton meter, misalignment of the apparatus, or contact between the object and container walls.
To minimise these:
Zero the balance or newton meter before each reading.
Ensure the object is fully submerged but not touching the bottom or sides.
Use the same liquid temperature and fluid depth for repeated trials.
Documenting these controls also helps justify the reliability of the experimental method in an exam or report.
Practice Questions
Question 1 (2 marks)
A student uses a eureka can to measure the volume of an irregular metal object.
Explain how the student can use this apparatus to determine the density of the metal.
Mark scheme:
(1 mark) The object is completely submerged in the eureka can and the volume of displaced water is collected and measured.
(1 mark) The mass of the object is measured with a balance and density = mass ÷ volume is calculated.
Question 2 (5 marks)
A student investigates the upthrust on an object when it is fully submerged in water. The object is suspended from a newton meter and readings are taken for its weight in air and when immersed in water.
(a) Explain how the student can determine the upthrust acting on the object. (2 marks)
(b) The volume of the object is 1.2 × 10⁻⁴ m³. Use your answer from (a) to show how the student can verify Archimedes’ principle. (3 marks)
Mark scheme:
(a)
(1 mark) Measure the weight in air and apparent weight in water using the newton meter.
(1 mark) The upthrust is equal to the difference between these two readings.
(b)
(1 mark) Upthrust should equal the weight of the displaced water, given by ρ × g × V.
(1 mark) Substituting ρ = 1000 kg m⁻³, g = 9.81 m s⁻², and V = 1.2 × 10⁻⁴ m³ gives an expected upthrust of approximately 1.18 N.
(1 mark) If this calculated value matches the measured upthrust within experimental uncertainty, it confirms Archimedes’ principle.

