OCR Specification focus:
‘Recall and derive Ek = ½mv² from first principles for translational motion.’
Kinetic energy is the energy an object possesses due to its motion. Understanding its origin and derivation from first principles links force, work, and motion together conceptually.
Understanding Kinetic Energy
Kinetic energy is one of the most fundamental forms of mechanical energy. It quantifies how much energy a moving object has as a result of its motion. The faster an object moves or the greater its mass, the more kinetic energy it possesses. This section explores the definition of kinetic energy, its connection to work and motion, and how the equation Ek = ½mv² is derived from basic physical principles.
Kinetic Energy: The energy a body has due to its motion.
The concept of kinetic energy provides a bridge between the dynamics of motion (forces and acceleration) and the energetics of a system (how energy changes and transfers). It plays a key role in describing systems ranging from moving particles to planets orbiting stars.
Linking Work and Energy
The work–energy principle states that the net work done on an object equals the change in its kinetic energy. Work, in this context, is a measure of energy transfer caused by a force acting over a distance. When a force causes an object to accelerate, energy is transferred into kinetic energy.
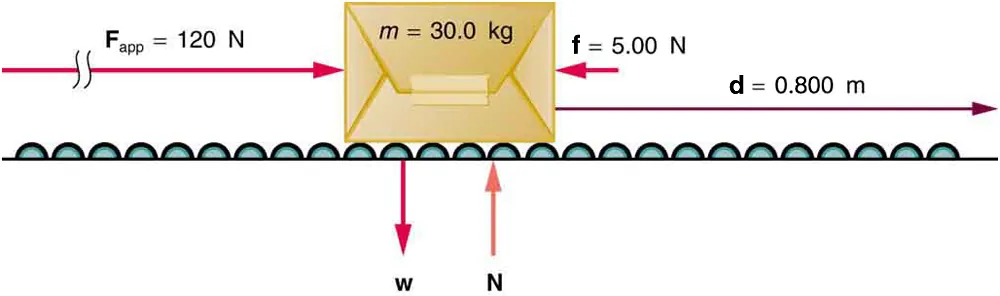
A package is pushed with a horizontal force over a distance ddd, while friction opposes the motion. Only the force components parallel to the displacement do work; the vertical pair NNN and www do no work here. This illustrates the work–energy link used to derive Ek=12mv2E_k=\tfrac12mv^2Ek=21mv2 for translational motion. Source.
EQUATION
—-----------------------------------------------------------------
Work Done by a Force (W) = Force × Displacement × cosθ
W = F s cosθ
W (J) = Work done, measured in joules
F (N) = Force applied, measured in newtons
s (m) = Displacement, measured in metres
θ = Angle between force and direction of motion
—-----------------------------------------------------------------
In this subsubtopic, we consider motion along a straight line, where the force acts in the same direction as motion, so θ = 0° and cosθ = 1. Therefore, W = F s.
A force–displacement plot where the area under the curve equals the work done by the force. For a constant force, the area is a rectangle W=FsW=F sW=Fs; for a varying force, the total work is the summed area of thin strips. This graphical view supports the transition from work to kinetic energy in the derivation of Ek=12mv2E_k=\tfrac12mv^2Ek=21mv2. Source.
When the force causes an acceleration, the work done increases the object’s kinetic energy. This relationship underpins the derivation of the formula for kinetic energy.
Deriving the Kinetic Energy Formula from First Principles
The derivation begins with Newton’s Second Law of Motion, which relates force, mass, and acceleration: F = ma. Combining this with the definition of work allows us to find an expression for the energy gained as an object accelerates from rest to a velocity v.
Step-by-step derivation
Start with the definition of work
Work done on the object: W = F s
Substitute for force using Newton’s Second Law:
F = ma, so W = ma s
Relate displacement and velocity using a kinematic equation (assuming constant acceleration):
v² = u² + 2as, where u is the initial velocity and v the final velocity
Rearrange to express displacement: s = (v² – u²) / 2a
Substitute this into the work equation:
W = ma × (v² – u²) / 2a
Simplify the expression:
The acceleration terms cancel: W = ½m(v² – u²)
This shows that the net work done equals the change in kinetic energy. For an object starting from rest (u = 0), the work done becomes W = ½mv². Therefore, kinetic energy (Ek) is given by:
EQUATION
—-----------------------------------------------------------------
Kinetic Energy (Ek) = ½ m v²
Ek (J) = Kinetic energy, measured in joules
m (kg) = Mass of the object
v (m s⁻¹) = Velocity of the object
—-----------------------------------------------------------------
This result demonstrates how the familiar equation for kinetic energy arises directly from the relationship between work, force, and motion.
Interpretation and Significance
The equation Ek = ½mv² shows that kinetic energy depends quadratically on velocity. This means that doubling the speed of an object increases its kinetic energy by a factor of four. Similarly, kinetic energy is directly proportional to mass: doubling the mass doubles the kinetic energy at the same speed.
This relationship reflects the mechanical behaviour of systems: a small increase in velocity requires a disproportionately larger increase in energy. This principle has important implications in transport, collisions, and energy efficiency.
Work–Energy Principle: The net work done on an object equals the change in its kinetic energy.
The principle provides a quantitative method for analysing motion when forces and displacements are involved, allowing physicists to describe real-world phenomena such as braking distances, projectile motion, or energy loss due to friction.
Translational Motion and Energy Transfer
In this subsubtopic, the motion considered is translational, meaning the object moves in a straight line without rotation. The kinetic energy derived here refers only to this type of motion. In later topics, rotational kinetic energy will be treated separately.
Energy transfer in this context occurs through mechanical work — the process by which a force acting over a distance changes an object’s energy state. When an object accelerates, chemical or electrical energy (for example, from a car engine or motor) is transformed into kinetic energy.
If positive work is done on the object, its kinetic energy increases.
If negative work (for example, from friction) is done, kinetic energy decreases.
When no net work is done, the kinetic energy remains constant, corresponding to motion at a steady velocity.
This interpretation allows energy changes to be traced through any mechanical system using the same basic principles.
Energy as a Scalar Quantity
Kinetic energy is a scalar quantity, meaning it has magnitude but no direction. While velocity is a vector quantity, squaring it in the kinetic energy formula removes the direction, leaving only magnitude. As a result, kinetic energy is always positive or zero, never negative.
The absence of direction simplifies energy analysis, making it useful for evaluating systems where multiple forces act in different directions.
Scalar Quantity: A physical quantity that has magnitude only and no direction.
Understanding that energy is scalar ensures that students correctly interpret how energy adds or transfers in systems, without confusing it with directional quantities like force or momentum.
Summary of Key Relationships
Force causes acceleration, producing displacement and performing work.
Work done equals the change in kinetic energy, forming the basis of energy conservation in motion.
Kinetic energy increases with both mass and the square of velocity, showing the sensitivity of energy to changes in speed.
Ek = ½mv² applies to translational motion and is derived directly from first principles using Newton’s laws and kinematic relationships.
FAQ
Kinetic energy depends on the square of velocity because it originates from the relationship between work and motion. When a constant force accelerates an object, both the distance travelled and the velocity increase linearly with time. Multiplying these together in the work calculation results in a quadratic dependence on velocity.
This means that a small increase in speed causes a large increase in kinetic energy. For example, doubling velocity quadruples the energy, which explains why high-speed collisions cause significantly more damage.
Yes. An object moving at constant velocity has kinetic energy even when the net force acting on it is zero.
The absence of a net force simply means there is no change in kinetic energy — not that kinetic energy is absent. In this case, the object maintains its existing kinetic energy because there is no acceleration or deceleration to transfer energy in or out of its motion.
Yes. Kinetic energy is not absolute; it depends on the observer’s frame of reference.
For example, a car travelling at 20 m s⁻¹ relative to the ground has kinetic energy in that frame. However, to a passenger inside the car, its kinetic energy is zero because, relative to them, the car isn’t moving.
This highlights that kinetic energy, unlike mass, is frame-dependent and must always be defined relative to a chosen reference point.
Kinetic energy is based on the square of velocity (v²), which is always positive or zero. The squaring process removes any directional information associated with the velocity vector.
If an object is stationary (v = 0), kinetic energy = 0 J.
If it moves, v² is positive, so kinetic energy is positive.
Negative kinetic energy would imply a negative magnitude of motion, which is physically meaningless because energy represents the capacity to do work, not a direction.
Students often make several small but critical errors when deriving this expression:
Forgetting that force and displacement must act in the same direction for W = F s to apply directly.
Ignoring that the derivation assumes constant acceleration and straight-line motion.
Confusing work done with power or impulse.
It’s also common to incorrectly assume that the ½ in the equation arises from dividing by two forces or distances, rather than from the mathematical relationship between acceleration, velocity, and displacement in the derivation.
Practice Questions
Question 1 (2 marks)
A car of mass 1200 kg is moving at a speed of 15 m s⁻¹. Calculate its kinetic energy.
Mark scheme:
Substitution into formula Ek = ½mv² (1 mark)
Ek = ½ × 1200 × (15)²Correct answer with unit: 1.35 × 10⁵ J (1 mark)
Question 2 (5 marks)
A student releases a trolley of mass 2.0 kg from rest on a smooth, horizontal surface. A constant horizontal force of 5.0 N acts on the trolley for a distance of 3.0 m.
(a) Calculate the work done on the trolley by the force. (2 marks)
(b) Using appropriate equations of motion, determine the final speed of the trolley after it has moved 3.0 m. (3 marks)
Mark scheme:
(a)
Correct use of work formula W = F × s (1 mark)
Correct calculation: 5.0 × 3.0 = 15 J (1 mark)
(b)
Statement or use of work–energy principle: work done = change in kinetic energy (1 mark)
Substitution: 15 = ½ × 2.0 × v² → v² = 15 (1 mark)
Final answer with correct unit: v = 3.9 m s⁻¹ (1 mark)

