OCR Specification focus:
‘Recall and derive Ep = mgh in a uniform gravitational field; choose reference levels appropriately.’
Gravitational potential energy (GPE) describes the stored energy of an object due to its position in a gravitational field. It forms a core part of energy analysis in mechanics.
Understanding Gravitational Potential Energy
Gravitational potential energy is one of the most fundamental forms of potential energy. It represents the energy an object possesses because of its position relative to the Earth or another massive body. When an object is raised against gravity, work is done on it, and this work is stored as gravitational potential energy. Conversely, when it falls, the stored energy is released, often becoming kinetic energy.
Gravitational Potential Energy (GPE): The energy an object possesses because of its position in a gravitational field.
The concept of GPE allows us to describe energy transfers within a system and to predict motion in gravitational fields, assuming minimal energy losses.
Deriving the Equation Ep = mgh
The relationship between gravitational potential energy and height can be derived from the definition of work done by a force. Work done is the product of the force applied and the distance moved in the direction of that force. In a uniform gravitational field, the force due to gravity is constant and equal to the weight of the object, which is given by F = mg.
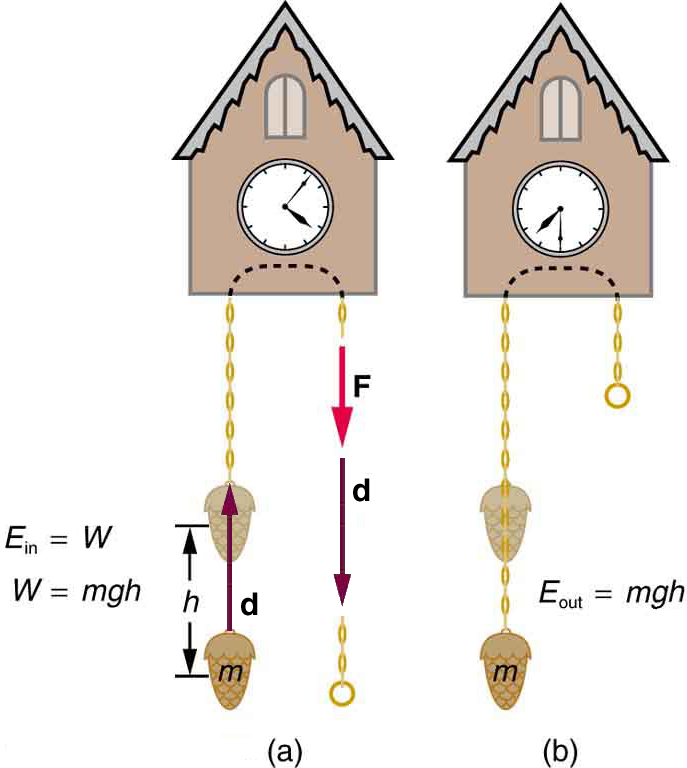
A mass is raised vertically through height h while a force equal to its weight mg is applied. The work done against gravity, W = mgh, is stored as gravitational potential energy. Vectors and labels make the energy-transfer pathway explicit. Source.
When an object of mass m is lifted vertically through a height h against the force of gravity, the work done on the object is given by:
EQUATION
—-----------------------------------------------------------------
Gravitational Potential Energy (Ep) = m g h
m = mass of the object (kilograms, kg)
g = gravitational field strength (newtons per kilogram, N kg⁻¹)
h = vertical height moved (metres, m)
—-----------------------------------------------------------------
This equation shows that the change in gravitational potential energy depends directly on the mass of the object, the gravitational field strength, and the vertical height change.
The Concept of Reference Levels
Gravitational potential energy is relative, not absolute. The value of Ep depends on where the zero of potential energy is chosen. This reference level can be chosen conveniently to simplify calculations.
Commonly, the ground level is taken as Ep = 0.
In some problems, a lower surface or a starting height may be defined as the reference level.
The difference in potential energy between two points is what has physical meaning, not the absolute value.
This flexibility means that only changes in Ep (ΔEp) influence the motion or energy transfers in mechanical systems.
Gravitational Field and Uniformity
The equation Ep = mgh is valid only in a uniform gravitational field, where g is constant. Near the Earth’s surface, this assumption holds well because variations in g with altitude are negligible for most everyday heights.
However, in contexts such as:
Spaceflight or planetary motion,
Large altitude changes,
the gravitational field strength varies, and the approximation of uniform g is no longer valid. In such cases, more general formulations using gravitational potential from Newton’s law of gravitation are required.
Within the A-Level scope, though, Ep = mgh is considered fully sufficient for all uniform-field problems.
Physical Interpretation
When an object is raised vertically, work must be done against the weight of the object. This work is stored as gravitational potential energy. The greater the height, the more energy is stored.
Key points to interpret Ep = mgh:
If h increases, Ep increases — energy is stored.
If h decreases, Ep decreases — energy is released.
If h is zero (reference level), Ep = 0.
If h is negative (below reference), Ep is negative, representing a position below the chosen zero level.
This sign convention helps describe motion relative to the chosen datum point, especially in problems involving energy conservation.
Linking GPE to Work Done and Energy Transfer
The increase in gravitational potential energy of an object equals the work done to raise it against gravity. Conversely, as the object falls, its potential energy is converted to kinetic energy, heat, or other forms depending on the context.
This link underpins the principle of conservation of energy, which ensures that energy cannot be created or destroyed — only transferred between forms.
Work Done: The energy transferred when a force moves an object through a distance in the direction of the force.
For a constant upward force equal to the object’s weight:
Work done = Force × Distance = mg × h = mgh
Hence, work done = change in gravitational potential energy.
This equality demonstrates that energy transfer and work done are equivalent quantities when dealing with gravitational effects in a uniform field.
The Role of g (Gravitational Field Strength)
The gravitational field strength g determines how much energy is required to lift an object through a certain height. On Earth, g ≈ 9.81 N kg⁻¹, but this value differs on other planets or celestial bodies.
For example:
On the Moon, g ≈ 1.6 N kg⁻¹
On Jupiter, g ≈ 24.8 N kg⁻¹
Thus, an object gains or loses different amounts of potential energy for the same height change depending on where it is located.
Energy Changes Between Points
When analysing a system involving movement between two heights, it is often useful to express the change in gravitational potential energy as:
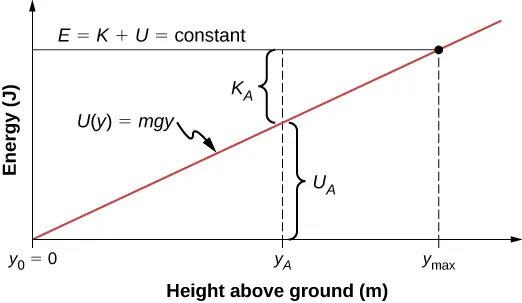
Potential energy U(y)=mgyU(y)=mgyU(y)=mgy is a straight line through the chosen reference level, illustrating the linear dependence on height. The plot also shows a constant total energy line and the partition between U and K. Extra detail: the total-energy line and kinetic-energy region go slightly beyond the syllabus but help visualise why only changes in Ep matter. Source.
EQUATION
—-----------------------------------------------------------------
Change in Gravitational Potential Energy (ΔEp) = m g (h₂ – h₁)
ΔEp = difference in energy between two vertical positions
h₁, h₂ = initial and final heights respectively (m)
—-----------------------------------------------------------------
This form highlights that only the change in height matters, reinforcing the importance of selecting a clear reference level.
Summary of Key Insights
Gravitational potential energy quantifies the energy stored due to an object’s height in a gravitational field.
The relationship Ep = mgh connects energy, mass, gravitational field strength, and height.
It is derived from the work done against the force of gravity in a uniform field.
The reference level determines the zero point for potential energy.
Only changes in Ep affect motion and energy transformations.
The equation is an essential foundation for analysing energy transfers, mechanical work, and motion under gravity at A-Level.
FAQ
If an object moves purely horizontally, its height relative to the chosen reference level does not change. Therefore, its gravitational potential energy remains constant.
Although Ep = mgh is unchanged, other energy forms (such as kinetic energy) may vary if forces act horizontally. Only vertical movement affects gravitational potential energy in a uniform field.
Potential energy is defined relative to a reference level, not absolutely.
Setting Ep = 0 at a convenient point—often the ground—simplifies calculations. The choice is arbitrary, as only changes in Ep (ΔEp) matter in physics. This means all real energy transfers depend on height differences, not on where zero is chosen.
No. In a uniform gravitational field, Ep depends only on the vertical height difference between two points.
Whether an object moves vertically or along an inclined plane, the change in Ep is identical if the vertical displacement is the same.
This property shows that gravitational force is a conservative force, meaning energy changes depend only on start and end positions.
Gravitational potential energy depends on g, which varies from planet to planet.
A smaller g (like on the Moon) means less Ep is gained for the same height change.
A larger g (like on Jupiter) means much more Ep for the same mass and height.
This variation explains why jumping feels easier on the Moon and why lifting objects on massive planets requires far more work.
When a lift moves upwards at constant speed, work is still done against gravity, and the lift’s Ep increases by mgh.
However, because the lift moves at constant velocity, its kinetic energy doesn’t change—the energy input from the motor exactly balances the work done against gravity and resistive forces.
If the lift moves downwards, the reverse occurs: gravitational potential energy decreases while the motor controls the descent safely.
Practice Questions
Question 1 (2 marks)
A 2.0 kg object is lifted vertically by 1.5 m in a region where the gravitational field strength is 9.8 N kg⁻¹.
Calculate the increase in the object’s gravitational potential energy.
Mark scheme:
Correct substitution into Ep = mgh (Ep = 2.0 × 9.8 × 1.5) → 1 mark
Correct answer Ep = 29.4 J (accept 29 J if rounded) with unit → 1 mark
Question 2 (5 marks)
A rock of mass 3.0 kg is dropped from rest from a height of 20.0 m above the ground.
(a) Calculate the loss in gravitational potential energy when the rock reaches the ground.
(b) Assuming air resistance is negligible, determine the speed of the rock just before it hits the ground.
(c) Explain what would happen to the energy values if air resistance were not negligible.
Mark scheme:
(a) Use Ep = mgh = 3.0 × 9.8 × 20.0 = 588 J → 1 mark
State that this is the loss in gravitational potential energy → 1 mark
(b) Apply conservation of energy: loss in Ep = gain in Ek → 1 mark
½mv² = 588 → v = √(2 × 588 ÷ 3.0) = 19.8 m s⁻¹ (accept 20 m s⁻¹) → 1 mark
(c) Explanation:
With air resistance, some energy is transferred to the surroundings as heat or sound, so kinetic energy gained < gravitational potential energy lost → 1 mark

