OCR Specification focus:
‘Analyse exchanges between gravitational potential energy and kinetic energy with minimal losses.’
Energy exchanges between gravitational potential energy (g.p.e.) and kinetic energy (k.e.) are central to understanding how moving and elevated objects interact within conservative systems under gravity.
Energy Exchange Between g.p.e. and k.e.
In many physical systems, energy constantly shifts between different forms while the total energy remains conserved. When an object moves vertically or along a slope, there is a continuous interchange between gravitational potential energy and kinetic energy. Understanding this exchange helps explain motion under gravity, from free-falling bodies to pendulums and roller coasters.
Gravitational Potential Energy (g.p.e.)
Gravitational potential energy represents the energy stored in an object due to its position in a gravitational field. When an object is elevated, work has been done against the force of gravity, giving it potential to do work when it falls.
Gravitational Potential Energy (g.p.e.): The energy possessed by an object due to its position in a gravitational field.
The reference level from which height is measured can be chosen conveniently (often the ground). Only differences in potential energy are physically meaningful.
EQUATION
—-----------------------------------------------------------------
Gravitational Potential Energy (Ep) = mgh
m = mass of object (kg)
g = gravitational field strength (N kg⁻¹)
h = height above reference level (m)
—-----------------------------------------------------------------
As an object’s height changes, its gravitational potential energy changes proportionally. The larger the mass or greater the height, the greater the stored g.p.e.
Kinetic Energy (k.e.)
Kinetic energy is the energy of motion, dependent on both mass and speed. When an object accelerates due to gravity, it gains kinetic energy while losing gravitational potential energy.
Kinetic Energy (k.e.): The energy associated with the motion of an object.
EQUATION
—-----------------------------------------------------------------
Kinetic Energy (Ek) = ½ mv²
m = mass of object (kg)
v = speed of object (m s⁻¹)
—-----------------------------------------------------------------
This expression shows that kinetic energy increases with the square of velocity, meaning even small increases in speed lead to significant increases in kinetic energy.
Energy Transformations in Free Fall
When an object falls freely under gravity (neglecting air resistance), gravitational potential energy is converted entirely into kinetic energy. The principle of conservation of energy ensures that total energy remains constant throughout the fall.
At the start of the fall:
The object has maximum g.p.e. and zero k.e.
During the fall:g.p.e. decreases as height decreases.
k.e. increases as velocity increases.
At the bottom:g.p.e. is minimal, and k.e. is maximal.
If air resistance is ignored, the total mechanical energy (g.p.e. + k.e.) remains unchanged. The conversion process can be represented as:
Loss in g.p.e. = Gain in k.e.
However, if resistive forces act, some energy transfers to the surroundings as thermal energy or sound, representing non-mechanical pathways and reducing the useful kinetic energy gained.
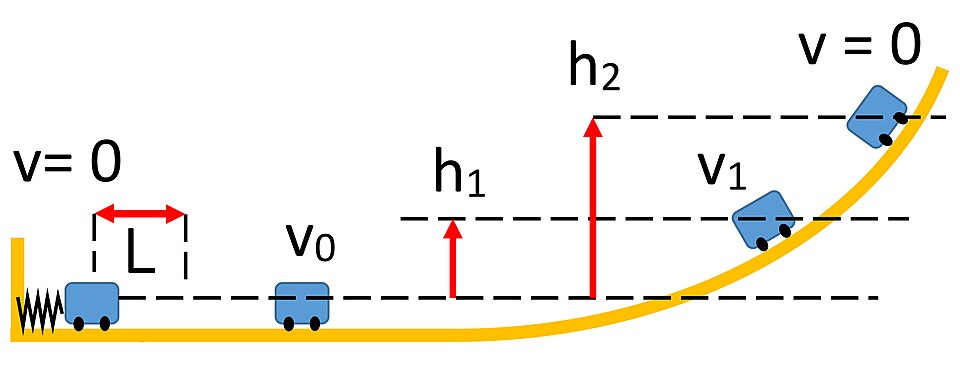
Energy Exchange on Inclined Paths
The same principles apply to motion along slopes or curved paths. For an object sliding down a ramp:
The component of gravitational force along the slope performs work on the object.
The rate of conversion between g.p.e. and k.e. depends on the slope’s angle and the presence of friction.
In an ideal smooth system (no friction), the conversion is complete and reversible.
When an object ascends a slope, the process reverses—kinetic energy is converted into gravitational potential energy until motion ceases or external work is applied.
The Role of the Conservation of Energy
The principle of conservation of energy is fundamental to understanding this exchange. It states that energy cannot be created or destroyed, only transformed from one form to another. In a closed system, the total mechanical energy remains constant provided no external forces (like friction or air resistance) do work.
EQUATION
—-----------------------------------------------------------------
Conservation of Mechanical Energy: Ep₁ + Ek₁ = Ep₂ + Ek₂
Ep₁, Ek₁ = initial energies
Ep₂, Ek₂ = final energies
—-----------------------------------------------------------------
This equation allows prediction of velocity, height, or other quantities when analysing motion under gravity. It demonstrates that the decrease in potential energy equals the increase in kinetic energy, assuming negligible losses.
Energy Losses and Real Systems
Real systems seldom exhibit perfect energy interchange. Common causes of energy loss include:
Air resistance, converting mechanical energy into heat.
Friction, especially in mechanical components like bearings or contact surfaces.
Deformation, such as bending or sound production during motion.
Despite these losses, energy is not destroyed but transferred to other stores, usually as internal energy of the surroundings. The total energy of the system and environment remains conserved, maintaining the law of conservation of energy.
Energy Diagrams and Tracking Transfers
Energy exchange can be visualised using energy flow diagrams or bar charts to show how energy moves between stores. These help students conceptualise conservation in complex systems such as pendulums, projectiles, or oscillations. Key transitions typically include:
Gravitational store → Kinetic store (falling or descending motion)
Kinetic store → Gravitational store (ascending motion or climbing)
Mechanical store → Thermal store (through resistive processes)
Tracking these transfers clarifies that the form of energy changes, not the quantity of total energy within the system and surroundings.
Application to Real-World Systems
Understanding energy exchange between g.p.e. and k.e. is essential for interpreting real-world systems such as:
Roller coasters, where height and speed changes continuously interconvert g.p.e. and k.e.
Schematic roller-coaster track illustrating interconversion of gravitational potential and kinetic energy along the path. The annotation “KE + PE = constant” emphasises conservation of mechanical energy for an idealised, low-loss system. Extra details beyond the syllabus are minimal. Source.
Pendulums, demonstrating periodic energy exchange with minimal loss in ideal conditions.

Diagram of a simple pendulum at multiple positions, indicating high gravitational potential energy at the extremes and maximum kinetic energy at the bottom. It visually summarises the reversible energy exchange in an ideal, low-loss system. No extra content beyond the syllabus is included. Source.
Hydroelectric systems, where falling water’s g.p.e. is transformed into k.e. and then electrical energy.
In all such systems, accurate modelling requires considering both ideal mechanical energy transfers and inevitable non-conservative losses.
Key Insight
The exchange between gravitational potential energy and kinetic energy underpins the dynamics of motion in a gravitational field. Through careful analysis of energy transformations and losses, physics enables precise quantitative predictions of motion and performance across both natural and engineered systems.
FAQ
The rate of conversion depends on the acceleration due to gravity (g) and the height through which the object falls. A larger value of g, such as on Jupiter compared to Earth, results in a faster conversion because the object accelerates more rapidly.
In the absence of resistive forces, this conversion occurs uniformly, and the velocity gained can be determined from v² = 2gh, showing that higher starting positions or stronger gravitational fields produce greater speeds at impact.
In real systems, some of the energy is inevitably transferred to other forms, such as heat, sound, or deformation energy, due to friction or air resistance.
In an ideal (frictionless) system, there are no external forces doing work against motion, so the sum of gravitational potential energy and kinetic energy remains constant. Once resistive forces are introduced, the system is no longer closed, and mechanical energy is not conserved even though total energy (including thermal and sound) still is.
The reference level sets where gravitational potential energy is defined as zero, and this choice is completely arbitrary.
If you choose the ground as zero, objects above it have positive g.p.e.
If you choose a point higher than the object, its g.p.e. may be negative.
Only changes in g.p.e. between two points have physical meaning, so the choice of reference level does not affect measurable outcomes or energy exchanges.
At the top of its trajectory, the vertical component of velocity is zero, so vertical kinetic energy is zero. However, if the projectile has horizontal motion, it still possesses horizontal kinetic energy.
At that point, gravitational potential energy is at a maximum, and energy begins to convert back to kinetic energy as it descends. The total mechanical energy (g.p.e. + k.e.) remains constant if air resistance is neglected.
In ideal systems, such as a frictionless pendulum, energy transfers between g.p.e. and k.e. occur without any loss to other stores.
This means:
As the object rises, k.e. is fully converted to g.p.e.
As it falls, g.p.e. is fully converted back to k.e..
Because no energy is dissipated, the motion continues indefinitely with the same amplitude. In real systems, resistive forces cause gradual energy loss, reducing amplitude over time and making the exchange irreversible.
Practice Questions
Question 1 (2 marks)
A small ball is dropped from rest from a height of 2.0 m above the ground. Ignore air resistance.
(a) Describe how the gravitational potential energy and kinetic energy of the ball change as it falls.
Mark scheme:
1 mark: States that gravitational potential energy decreases as the ball falls.
1 mark: States that kinetic energy increases as the ball’s speed increases (due to acceleration under gravity).
Question 2 (5 marks)
A 0.50 kg trolley starts from rest at the top of a smooth slope 1.2 m high. The trolley moves down the slope and reaches the bottom. Air resistance and friction are negligible.
(a) Calculate the gravitational potential energy lost by the trolley as it descends. (2 marks)
(b) State and explain what happens to this energy as the trolley reaches the bottom. (3 marks)
Mark scheme:
(a)
1 mark: Correct equation stated: Ep = mgh.
1 mark: Substitution and correct answer: (0.50 × 9.8 × 1.2) = 5.88 J ≈ 5.9 J.
(b)
1 mark: States that gravitational potential energy is converted to kinetic energy.
1 mark: Explains that as the trolley accelerates, its velocity increases, so kinetic energy rises.
1 mark: Mentions that in the absence of resistive forces, total mechanical energy remains constant (energy is conserved).

