OCR Specification focus:
‘Solve multistep problems combining Ek and Ep; avoid sign errors and inconsistent reference points.’
Understanding how kinetic energy and gravitational potential energy interact in physical systems is essential for analysing motion, energy conservation, and mechanical processes accurately. Mismanaging reference levels and signs often causes conceptual and numerical errors.
Energy Relationships in Mechanics
The study of mechanical energy focuses on how energy is stored, transferred, and transformed within a system. For OCR A-Level Physics, the main concern in this section is how gravitational potential energy (g.p.e.) and kinetic energy (k.e.) convert between each other under the principle of conservation of energy in idealised systems.
In an isolated mechanical system, with no external work or frictional losses, the total mechanical energy remains constant. Thus, when one form of energy increases, the other decreases proportionally.
The Key Energy Forms
Kinetic Energy
Kinetic energy is the energy of motion. It depends on an object’s mass and speed.
Kinetic Energy: The energy a body possesses due to its motion, given by Ek = ½mv².
Kinetic energy is always positive, as mass and the square of velocity are both positive quantities. When speed increases, the kinetic energy rises exponentially.
EQUATION
—-----------------------------------------------------------------
Kinetic Energy (Ek) = ½mv²
m = Mass of the object (kg)
v = Velocity of the object (m s⁻¹)
—-----------------------------------------------------------------
Gravitational Potential Energy
Gravitational potential energy (Ep) represents the energy stored due to an object’s position in a gravitational field. The energy depends on the object’s mass, the gravitational field strength, and the height relative to a chosen reference level.
Gravitational Potential Energy: The energy an object has because of its position in a gravitational field, given by Ep = mgh.
EQUATION
—-----------------------------------------------------------------
Gravitational Potential Energy (Ep) = mgh
m = Mass of the object (kg)
g = Gravitational field strength (N kg⁻¹)
h = Height relative to reference level (m)
—-----------------------------------------------------------------
Analysing Energy Exchanges
When an object moves vertically, there is a direct energy exchange between kinetic and gravitational potential energy. As the object descends, its g.p.e. decreases while its k.e. increases, and vice versa when rising.

A labelled pendulum diagram showing Ep highest at the extremes and Ek highest at the lowest point, with continuous exchange between the two. This illustrates conservation of mechanical energy in an idealised system with negligible losses. The diagram’s simplicity supports correct sign use by treating energies as positive scalars. Source.
In an ideal closed system, without air resistance or friction:
Total mechanical energy remains constant.
The sum of Ek and Ep is the same at all points during motion.
Any change in one form is balanced by an equal and opposite change in the other.
This can be expressed as:
EQUATION
—-----------------------------------------------------------------
Conservation of Mechanical Energy: Ek + Ep = Constant
Ek = Kinetic energy (J)
Ep = Gravitational potential energy (J)
—-----------------------------------------------------------------
This equation provides the foundation for solving multistep problems, where energy transitions must be tracked carefully between states of motion and height.
Common Multistep Problem Structures
Students often encounter problems involving:
Vertical motion such as objects thrown upwards or dropped.
Inclined planes, where part of the motion is horizontal but gravitational effects remain significant.
Pendulum motion, where energy continuously transfers between kinetic and potential forms.
In these problems, it is critical to:
Identify all energy states clearly — initial and final positions.
Select an appropriate reference level for gravitational potential energy.
Apply the conservation of energy principle quantitatively to connect changes in Ek and Ep.
Substitute known values carefully and verify consistency of units.
Choosing Reference Levels
Errors frequently occur due to inconsistent reference points for height. Because g.p.e. is relative, the choice of where h = 0 is arbitrary, but it must be used consistently throughout the problem.
For example:
In free-fall, it is often convenient to take the ground level as h = 0.
In oscillating or projectile motion, the lowest point is typically chosen as the reference.
The actual values of g.p.e. depend on this reference, but changes in energy—which determine motion—do not. Hence, consistent reference choice prevents sign errors and maintains physical validity.
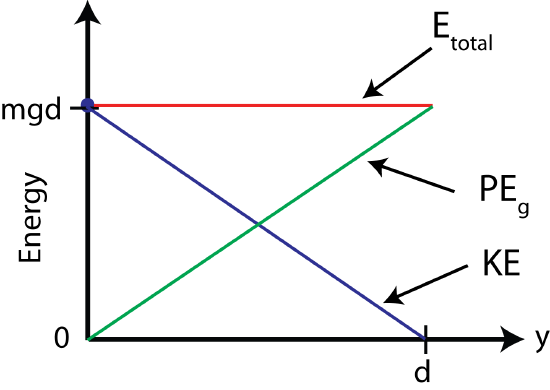
A plot showing Ep increasing linearly with height, Ek decreasing correspondingly, and Etot as a horizontal constant. The figure explicitly sets a zero-height origin, underscoring that reference choice is arbitrary but must be used consistently to avoid sign mistakes. This aligns with conservation of mechanical energy in a closed system. Source.
Avoiding Sign Errors
Sign conventions are a major source of mistakes in energy calculations.
To avoid them:
Treat g (gravitational field strength) as a positive magnitude, not a directional quantity, when using Ep = mgh.
If height decreases, interpret this as a loss of potential energy (negative change), not a negative height.
When substituting velocity, always use the magnitude of speed in Ek = ½mv².
Incorrectly mixing direction signs with scalar energy values leads to contradictory or physically impossible results.
Understanding Energy Conservation in Context
The energy exchange between kinetic and gravitational potential energy assumes negligible non-conservative forces. However, in real situations such as air resistance or friction, mechanical energy decreases due to transformation into thermal energy. In such cases, total energy (including all forms) is conserved, but mechanical energy alone is not.
OCR students should focus on recognising whether a system is closed or open, as this determines whether energy losses must be considered explicitly.
Diagnostic Tips for Error Prevention
To ensure precision in multistep problems:
Draw an energy diagram showing Ek and Ep at each key point.
Label the reference height and mark increases or decreases in energy.
Check dimensional consistency in all terms (energy in joules).
Interpret zero and negative results correctly: zero energy may mean rest or reference height, not necessarily absence of motion.
Additionally, always review whether the energy terms used correspond to the same object and reference level throughout your calculation steps.
Summary of Key Relationships
Kinetic energy depends on speed: Ek = ½mv².
Gravitational potential energy depends on height: Ep = mgh.
Total mechanical energy (Ek + Ep) remains constant in the absence of energy losses.
Energy exchanges reflect changes in motion and position.
Consistency in reference levels and sign conventions is essential for accurate results.
By mastering these principles, students can confidently analyse systems involving motion under gravity, ensuring clarity, correctness, and physical understanding in all multistep energy problems.
FAQ
Although kinetic energy (Ek) and gravitational potential energy (Ep) vary during motion, their sum remains constant in a closed system.
This happens because energy is only transferred, not created or destroyed. As an object falls, the loss in Ep exactly equals the gain in Ek, keeping the total mechanical energy the same.
If friction or air resistance acts, some mechanical energy converts to heat or sound, breaking the ideal conservation and lowering total mechanical energy.
No — kinetic energy is always positive because it depends on the square of velocity, ½mv².
While velocity itself can be positive or negative depending on direction, squaring it removes the sign. Thus, kinetic energy represents the magnitude of motion, not its direction.
Negative energy changes, however, may appear in calculations to show a loss in kinetic energy when an object slows down.
Changing the zero level of gravitational potential energy shifts all Ep values by a constant amount, but energy differences remain unchanged.
This means physical predictions such as speed, acceleration, or total mechanical energy are unaffected by the choice of reference.
To avoid confusion, consistently use one reference level — such as the ground or the lowest point in motion — throughout a problem.
Using a negative height can cause sign inconsistencies, especially when interpreting energy changes.
Instead of giving height a sign, treat energy changes as positive or negative depending on whether energy is gained or lost.
For instance:
A fall from 2 m to 0 m represents a loss of potential energy, not a negative height.
This approach keeps calculations consistent with scalar energy quantities.
If total mechanical energy appears to change, check for:
Energy losses through non-conservative forces like friction or drag.
Incorrect sign conventions, especially for height or direction.
Inconsistent reference points between energy states.
In realistic systems, apparent energy loss often indicates that part of the energy has been converted into thermal energy, sound, or deformation, rather than being destroyed.
Practice Questions
Question 1 (2 marks)
A ball of mass 0.40 kg is dropped from rest from a height of 2.5 m above the ground.
Ignore air resistance.
(a) Calculate the speed of the ball just before it hits the ground.
Use g = 9.8 m s⁻².
Mark Scheme – Question 1
Correct use of conservation of energy: mgh = ½mv² or equivalent (1 mark)
Correct calculation of v = √(2gh) = √(2 × 9.8 × 2.5) = 7.0 m s⁻¹ (accept 6.9–7.1 m s⁻¹) (1 mark)
Question 2 (5 marks)
A small object of mass 0.15 kg slides down a smooth ramp inclined at 30° to the horizontal. The object starts from rest at a height of 0.80 m above the bottom of the ramp.
(a) Calculate:
(i) the gravitational potential energy lost by the object,
(ii) the kinetic energy gained by the object at the bottom of the ramp.
(b) Explain why the kinetic energy at the bottom may be less than your calculated value if the ramp is not perfectly smooth.
Mark Scheme – Question 2
(a)(i)
Correct equation: Ep = mgh (1 mark)
Substitution: Ep = 0.15 × 9.8 × 0.80 (1 mark)
Correct answer: 1.18 J (accept 1.2 J) (1 mark)
(a)(ii)
Statement that in absence of friction, Ek = Ep lost (1 mark)
Correct value: Ek = 1.18 J (1 mark)
(b)
Explanation that friction or air resistance converts some mechanical energy into heat or sound, reducing kinetic energy (1 mark)

