One-sided limits evaluated algebraically and graphically (1.5.3) | AP Calculus AB Notes

AP Syllabus focus:
‘Determine one-sided limits analytically using limit laws and connect the results to graphical behavior of the function near the point of interest.’

One-sided limits describe how a function behaves as the input approaches a point from only the left or only the right, allowing precise analysis of directional behavior and continuity.

Understanding One-Sided Limits

One-sided limits deepen the study of function behavior by focusing on directional approach. A one-sided limit refers to the value a function appears to approach as x approaches a point c exclusively from the left (denoted $x \to c^{-}$ ) or from the right (denoted $x \to c^{+}$ ). These directional perspectives are essential for identifying subtle changes in behavior, evaluating continuity, and analyzing functions defined piecewise or with abrupt transitions. Because they capture behavior along a single direction, one-sided limits often reveal structural features that a two-sided limit might conceal.

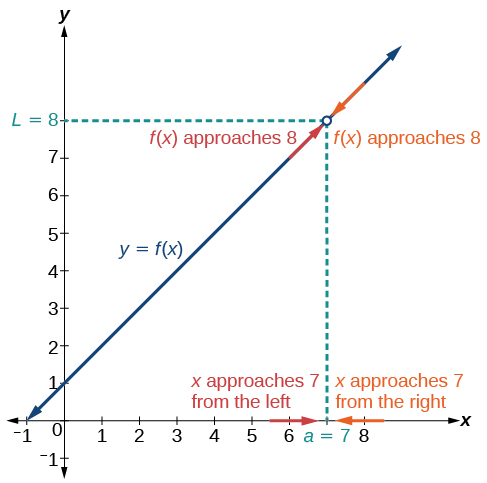
This graph illustrates a function approaching the same value from both sides of x=7x, emphasizing that one-sided limits describe directional behavior even when the function is undefined at the point. Source.

One-Sided Limit: A limit describing the value a function approaches as the input approaches a point from only one direction—either from the left or from the right.

One-sided limits also allow algebraic techniques to be used more selectively. When analyzing complicated expressions, students apply limit laws to each directional approach separately, ensuring that the function's structure is consistent with the direction from which x approaches.

Algebraic Evaluation of One-Sided Limits

Algebraic techniques offer precise tools for evaluating one-sided limits when the functional expression is known. These techniques apply the standard limit laws—such as those for sums, differences, products, and quotients—to the directional context.

When Algebraic Methods Are Most Effective

Algebraic evaluation is especially powerful when the function is expressed as a combination of elementary functions whose limits are already known to be continuous across their domains. To determine a one-sided limit algebraically, the following strategies are commonly applied:

Substitute values approaching the target point from the appropriate direction when the function is continuous at that point.
Apply limit laws to break a complex expression into simpler parts when each directional limit exists.
Factor or simplify an expression to expose behavior that is obscured in its original form.
Identify cases where the numerator or denominator creates directional differences, such as with absolute value or piecewise definitions.

$\lim_{x \to c^{-}} f(x) = L$
$x \to c^{-}$ = x approaches c from values less than c
$L$ = the value the function approaches

A single sentence here ensures separation between equation blocks while maintaining conceptual flow.

$\lim_{x \to c^{+}} f(x) = L$
$x \to c^{+}$ = x approaches c from values greater than c
$L$ = the value the function approaches

These algebraic expressions clarify that the direction of approach is an inherent part of the notation. Choosing the correct sign in the superscript depends entirely on the domain and the behavior of the function near the point of interest.

Graphical Interpretation of One-Sided Limits

Graphical reasoning complements algebraic methods by providing visual confirmation of directional behavior. Students examine how the graph behaves as it nears the target x-value from one side. Because graphs illustrate trends and discontinuities, they play an important role in interpreting results obtained analytically.

Identifying Directional Behavior on Graphs

A graph displays information about one-sided limits through the shape and trajectory of the curve near a point. Features to observe include:

Whether the left-hand graph segment approaches a particular y-value as x moves toward the point.
Whether the right-hand graph segment approaches the same or a different value.
Whether the graph shows a jump, hole, or vertical asymptote, each of which affects the existence or value of a one-sided limit.

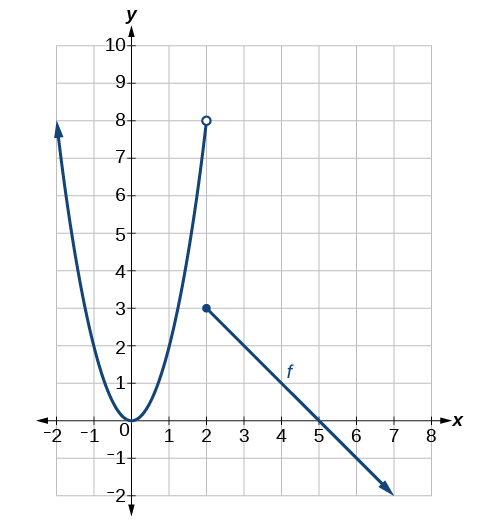
As x approaches 2 along the curved branch, the function approaches the open-circle value near 8. However, the filled point at (2,3) defines the actual function value, highlighting a removable discontinuity and reinforcing that limits depend on nearby values, not the function’s assigned value. Source.

Whether the function is defined differently on each side, as this may create mismatched one-sided limits.

Graphical analysis reinforces the idea that limits concern approach, not necessarily function values.

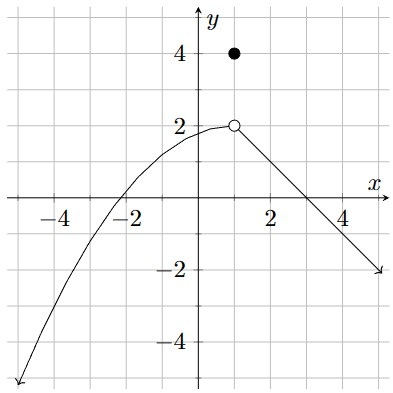
The graph shows that the function approaches a value of 2 from both sides as x approaches 1, even though the function value at x=1 is defined to be 4. This illustrates that a limit depends on nearby behavior rather than the function’s actual value at the point. Source.

Connecting Algebraic and Graphical Approaches

The specification emphasizes relating algebraic findings to graphical observations. This connection strengthens conceptual understanding by ensuring that students do not rely solely on symbolic manipulation. When both methods are aligned, students gain confidence that the limit laws have been applied correctly. When they disagree, the discrepancy often indicates an overlooked feature such as a domain restriction or piecewise transition.

Understanding these relationships prepares students for future topics involving continuity, differentiability, and rigorous analysis of dynamic change in functions.

FAQ

One-sided limits clarify whether each side of a function approaches the same value, allowing you to distinguish between removable and jump discontinuities.

If both one-sided limits agree but differ from the function value, the discontinuity is removable.
If they disagree, the discontinuity is a jump, even if the function happens to be defined at the point.

Two-sided limits concern behaviour at a single target point, while one-sided limits consider directional approach. Functions may align at one specific point yet diverge in structure elsewhere.

A function could be piecewise with separate left and right definitions, leading to different one-sided behaviour at other boundaries even if they match at the chosen point.

Several algebraic structures naturally produce directional differences:

• Absolute value expressions
• Piecewise definitions
• Rational expressions with factors that switch sign on either side of a point
• Functions involving roots that restrict the domain

These features can cause different behaviour depending on whether x approaches from below or above the target value.

Yes. Graphical imprecision affects interpretation but not the mathematical definition of the limit.

If the function’s rule or a more detailed graph confirms a clear trend from one side, the one-sided limit is determined by that behaviour, not by the drawing’s accuracy.

However, poorly scaled or low-resolution graphs can give misleading impressions, so numerical or algebraic checks are recommended.

The derivative is built from a limit that examines the behaviour of the difference quotient as the interval shrinks.

One-sided limits help ensure that the instantaneous rate of change is well defined, especially for functions with corners or cusps.

If the left-hand and right-hand derivative limits differ, the derivative does not exist at that point, even though the function may still have a well-defined one-sided limit.

Practice Questions

Question 1 (1–3 marks)
The graph of a function f is shown near x = 2. As x approaches 2 from the left, the graph approaches the y-value 5. As x approaches 2 from the right, the graph approaches the y-value 3.
(a) State the value of the limit of f(x) as x approaches 2 from the left.
(b) State the value of the limit of f(x) as x approaches 2 from the right.
(c) Determine whether the two-sided limit of f(x) as x approaches 2 exists. Give a reason for your answer.

Question 1
(a) 1 mark: Correct value stated as 5.
(b) 1 mark: Correct value stated as 3.
(c) 1 mark: Correct conclusion that the two-sided limit does not exist because the one-sided limits are not equal.

Total: 3 marks.

Question 2 (4–6 marks)
A function g is defined as follows:
g(x) = 4 – x for x < 1
g(x) = kx + 1 for x ≥ 1

(a) Find the left-hand limit of g(x) as x approaches 1.
(b) Find the right-hand limit of g(x) as x approaches 1.
(c) Determine the value of k that makes g continuous at x = 1.
(d) Using your value of k, explain whether both one-sided limits at x = 1 are equal and how this relates to the continuity of g.

Question 2
(a) 1 mark: Left-hand limit correctly found as 4 – 1 = 3.
(b) 1 mark: Right-hand limit correctly expressed as k(1) + 1 = k + 1.
(c) 2 marks:
• 1 mark for setting the equality 3 = k + 1 to ensure continuity.
• 1 mark for solving correctly to obtain k = 2.
(d) 2 marks:
• 1 mark for stating that both one-sided limits equal 3 when k = 2.
• 1 mark for explaining that equality of one-sided limits means the limit exists and matches the function value, confirming continuity at x = 1.

Total: 6 marks.

Try All Topic Practice Questions

Written by:

Dr Rahil Sachak-Patwa

Oxford University - PhD Mathematics

Rahil spent ten years working as private tutor, teaching students for GCSEs, A-Levels, and university admissions. During his PhD he published papers on modelling infectious disease epidemics and was a tutor to undergraduate and masters students for mathematics courses.