Understanding derivative notation is essential for interpreting how a quantity changes with respect to another, allowing students to connect symbolic forms with graphical behavior and contextual meaning.

Interpreting Derivative Notation

Derivative notation communicates how a function’s output changes relative to its input. Each notation reflects the instantaneous rate of change, emphasizing how sensitive the function value is to small variations in the input. In AP Calculus AB problems, students must recognize these notations across formulas, graphs, and real-world settings and understand that they all represent the same underlying concept.

The Function Notation f′(x)

When a function is written as $f(x)$, its derivative is denoted by $f′(x)$, meaning the derivative of $f$ with respect to $x$. This notation highlights the derivative as a new function with its own set of inputs and outputs.

Because $f′(x)$ is itself a function, it can be evaluated, graphed, or substituted into expressions just like the original function. Students will often encounter statements such as “find $f′(3)$” or “determine where $f′(x)$ is positive,” each requiring interpretation grounded in rate-of-change meaning.

The Notation y′ and Its Use in Equations

In equations where the dependent variable is written explicitly as $y$, the derivative is written as $y′$, pronounced “y prime.” This notation is compact and frequently used when $y$ is defined by an explicit formula without naming a function.

Because $y′$ emphasizes the variable rather than the function name, it often appears in algebraic manipulations, differential equations, and expressions describing slope. This versatility makes the notation especially useful in symbolic work where the focus is on relationships rather than functional labels.

The Leibniz Notation dy/dx

The notation $dy/dx$ highlights the derivative as a ratio of differentials, reflecting how a small change in $x$ influences the corresponding change in $y$.

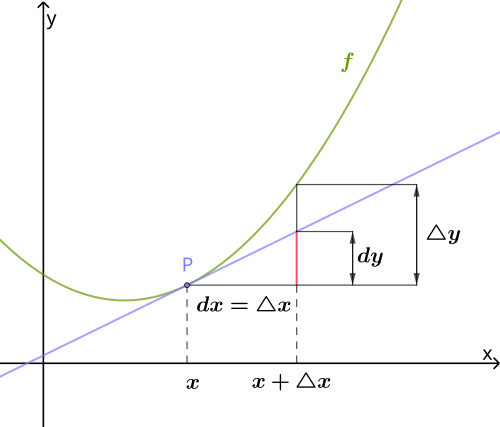
This diagram illustrates $dy$ as a linear response to a small change $dx$, highlighting the idea that the derivative $dy/dx$ measures the instantaneous change in output relative to input. It reinforces the interpretation of the derivative as a local linear approximation. Some advanced visual cues appear, but they are not required for AP Calculus AB. Source.

This notation is especially prevalent in word problems where relationships between variables carry practical meaning, such as speed, growth, or rates of accumulation. In such contexts, the structure of $dy/dx$ reinforces the idea of “change in output per unit change in input,” echoing units like meters per second or dollars per year.

Connections Among Derivative Notations

Although $f′(x)$, $y′$, and $dy/dx$ look different, they express the same mathematical idea. Recognizing when each is appropriate helps students move fluidly through various representations.

Use cases include:

• $f′(x)$ when working with named functions or matching functions to graphs.

• $y′$ when manipulating equations or expressing derivatives succinctly in symbolic contexts.

• $dy/dx$ when interpreting rates in real-world tasks or applying units to derivative expressions.

Understanding these distinctions allows students to interpret derivative expressions accurately, regardless of the notation chosen in the problem.

Derivative Notation in Graphs

Students often encounter derivative notation when analyzing graphical behavior. For a graph of $y = f(x)$:

• $f′(x)$ corresponds to the slope of the tangent line at each point.

• Positive or negative derivative values describe whether the graph is rising or falling.

• The magnitude of $f′(x)$ communicates how steeply the graph changes.

Graphical tasks may ask students to estimate $f′(a)$ by observing the tangent line at $x = a$ or to determine intervals where the derivative is positive, zero, or negative.

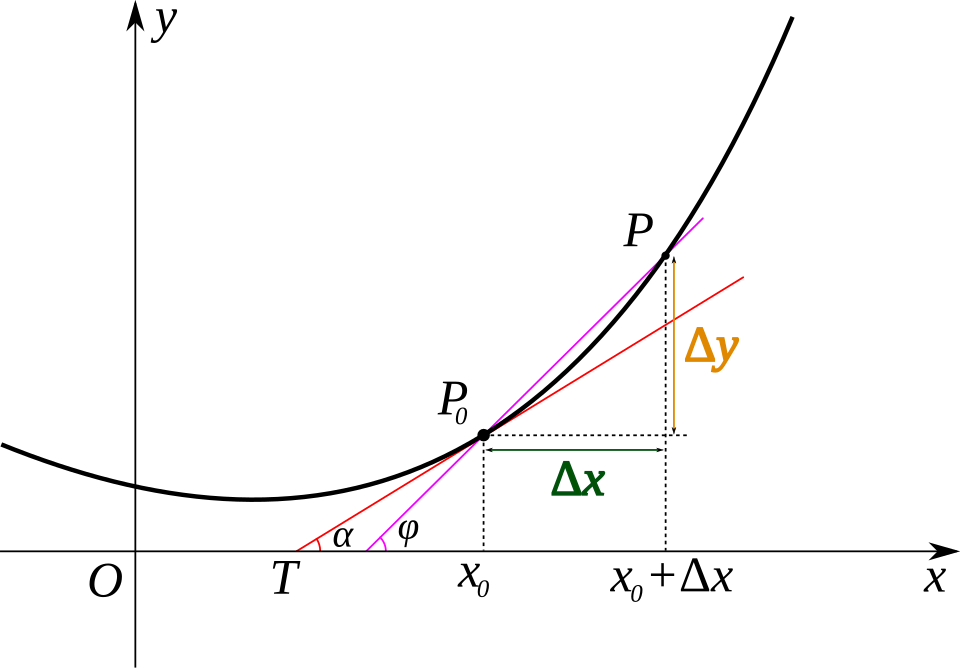
This diagram shows a function’s graph with a tangent line, illustrating the geometric meaning of the derivative as the slope of the tangent. The labeled components highlight changes in output relative to changes in input. Extra annotations support intuition but exceed what the syllabus strictly requires. Source.

Derivative Notation in Word Problems

In real-world applications, derivative notation reflects meaningful relationships between measurable quantities. Expressions such as $dy/dx = 5$ may indicate a growth rate, speed, or rate of consumption depending on the context.

Important features include:

• Units associated with $dy/dx$ reinforce its interpretation as a rate.

• Statements like “$f′(3) = -2$” signal decreasing output at a specified input value.

• Word problems may mix notations, requiring translation between symbols and verbal descriptions.

Summary of Notational Roles

To navigate AP Calculus AB problems effectively, students must identify derivative notation in multiple settings:

• Symbolic: manipulating expressions involving $f′(x)$, $y′$, or $dy/dx$.

• Graphical: associating notation with tangent-line slopes and qualitative behavior.

• Applied: interpreting derivatives as instantaneous rates with meaningful units.

Mastery of these forms enables students to interpret derivatives consistently and recognize their significance regardless of the notation presented.