The derivative function formalizes how a quantity changes at every input value, using limits to capture instantaneous change and produce a new function describing local behavior.

Defining the Derivative Function

The derivative function describes how a function’s output changes with respect to its input at each point where the limit-based definition exists.

The derivative function is foundational in calculus because it allows us to analyze variation across an entire domain rather than at a single point. When the limit exists for each relevant $x$, the result is a new function that encodes instantaneous rates of change.

Understanding the Limit Structure

The expression inside the derivative’s definition is called a difference quotient, and it measures how much the function changes over an interval of length $h$.

By shrinking the interval length $h$ toward zero, the difference quotient converges—when the limit exists—to a precise instantaneous rate.

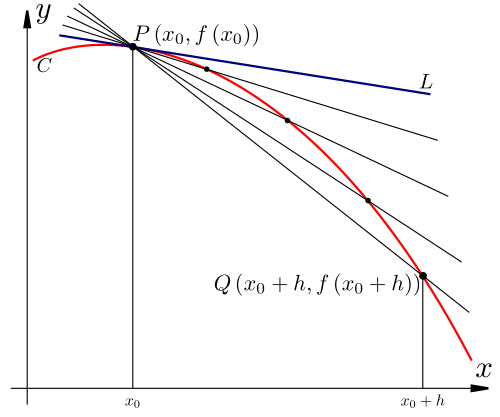
A curve C is shown with a secant line joining the points at x and x+h. As h becomes smaller, the secant line rotates toward the tangent line L, illustrating the limit process that defines the derivative. This visual emphasizes that $f'(x)$ is obtained as the limiting slope of secant lines as the two points on the graph merge into one. Source.

This limit-based viewpoint is essential because many real-world and mathematical processes rely on changes occurring over infinitesimally small intervals.

Equation Form of the Derivative Function

Students benefit from seeing the derivative written in standard symbolic form, which reinforces its structure and purpose.

This expression highlights the relationship between the original function and its derivative: the derivative evaluates how $f$ changes, while $f$ itself provides the base values from which those changes are measured.

Interpreting $f'(x)$ as a New Function

Once defined, the derivative is treated as a standard function that can be graphed, tabulated, or analyzed algebraically. Key interpretation points include:

• Domain considerations: $f'(x)$ is defined only where the limit exists.

• Continuity implications: Differentiability requires continuity, though continuity alone does not guarantee differentiability.

• Behavioral insights: The sign and magnitude of $f'(x)$ reveal whether $f$ is increasing or decreasing and how rapidly.

A derivative function often provides a more revealing view of behavior than the original function, especially when analyzing trends, turning points, and local linear approximations.

The Derivative as a Function of Local Behavior

The derivative represents the instantaneous rate of change, a concept that generalizes to multiple contexts such as velocity, growth rate, and sensitivity analysis. Even in abstract settings, the derivative quantifies how outputs respond to infinitesimal input changes.

This understanding reinforces why limits are essential: instantaneous behavior cannot be captured without letting interval lengths approach zero.

Connecting the Derivative to Graphs

Graphically, the derivative function describes the slope of the tangent line to the graph of $f$ at each point where the derivative exists.

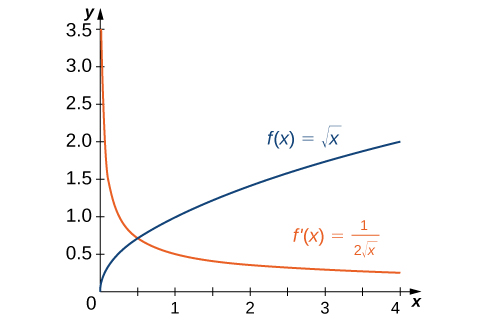
The graph of $f(x)=\sqrt{x}$ is plotted together with its derivative $f'(x)=\frac{1}{2\sqrt{x}}$. For each x in the domain, the value of $f'(x)$ gives the slope of the tangent line to the graph of f at that point. The steep tangent near x=0 corresponds to very large values of $f'(x)$ there, indicating a vertical tangent in the original graph. Source.

A tangent line provides the best linear approximation to the function near that point.

Students should note the following conceptual connections:

• The derivative reflects the steepness and direction of the function’s graph.

• Sharp corners or cusps may prevent the derivative from existing because the slope changes abruptly.

• Smoothness in the graph typically corresponds to a well-defined derivative.

These connections help students appreciate the derivative as both an algebraic and geometric idea.

Viewing the Derivative as a Limit-Generated Rule

Although later techniques allow differentiation without computing limits every time, it is crucial to recognize that all derivative rules stem from the limit definition. The limit form ensures consistency across functions and validates shortcuts like the power rule.

Important ideas include:

• Every derivative rule must agree with $\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}$.

• Limit-based reasoning ensures derivative formulas remain accurate for complex expressions.

• Understanding the definition supports troubleshooting when functions behave unexpectedly.

This grounding in limits strengthens conceptual mastery and prepares students for more advanced derivative applications.

Structural Overview of $f'(x)$ Across a Domain

The derivative function often reveals patterns that are less apparent in $f(x)$ itself.

Key observations:

• If f'(x) > 0, the function is locally increasing.

• If f'(x) < 0, the function is locally decreasing.

• If $f'(x) = 0$, the function may have a local extremum or a point of inflection, depending on broader behavior.

These interpretations rely on the derivative being defined through limits, which guarantee precision in describing local variation.

The Central Role of Limits in Defining Derivatives

Limits ensure that the derivative function is not based on approximations but on exact instantaneous behavior. Without limits, one could only compute average changes, not instantaneous ones. By defining $f'(x)$ through the limit of a difference quotient, calculus establishes a rigorous, universally applicable framework for analyzing change.