Deriving the Power Rule from First Principles (2.5.1) | AP Calculus AB Notes

AP Syllabus focus:

‘Use the definition of the derivative as a limit of a difference quotient to compute derivatives of simple power functions and motivate the general power rule.’

This section introduces how the power rule emerges naturally from the limit definition of the derivative, showing why differentiation of power functions follows a predictable and generalizable pattern.

Derivatives from First Principles

The goal of this subsubtopic is to derive the familiar power rule using the fundamental limit-based definition of the derivative. To begin, recall that the derivative represents the instantaneous rate of change of a function at a point, computed through a limiting process.

Derivative (at a point): The limit of the average rate of change as the interval shrinks to zero.

Because this subsubtopic focuses specifically on power functions, we investigate how the derivative arises from algebraic manipulation of the difference quotient. The central object is the difference quotient, introduced when computing an average rate of change but now reppurposed to capture instantaneous behavior.

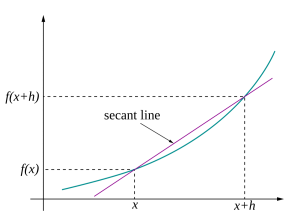
This diagram shows two points on a function connected by a secant line, whose slope represents the difference quotient. It visually demonstrates the average rate of change between x and x+h. As the interval shrinks, the secant slope approaches the slope of the tangent line, i.e., the derivative. Source.

$\text{Difference Quotient for } f(x) = \dfrac{f(x+h)-f(x)}{h}$

$h$ = Increment in the input

The derivative exists only when the limit of this expression as $h \to 0$ exists. Understanding this structure is important before examining how power functions behave.

Setting Up the Derivative of a Power Function

Let the function be $f(x)=x^n$ , where $n$ is a positive integer. We substitute this into the difference quotient and analyze how the expression simplifies. Central to this derivation is recognizing how the algebraic expansion of $(x+h)^n$ reveals the pattern that leads to the power rule. The usefulness of this approach lies in its ability to illustrate how the derivative formula emerges structurally rather than being taken as a memorized rule.

The Role of Algebraic Expansion

To fully derive the result, the expression $(x+h)^n$ must be expanded. This is where binomial structure becomes essential, because the expansion creates multiple terms involving powers of $x$ and $h$ .

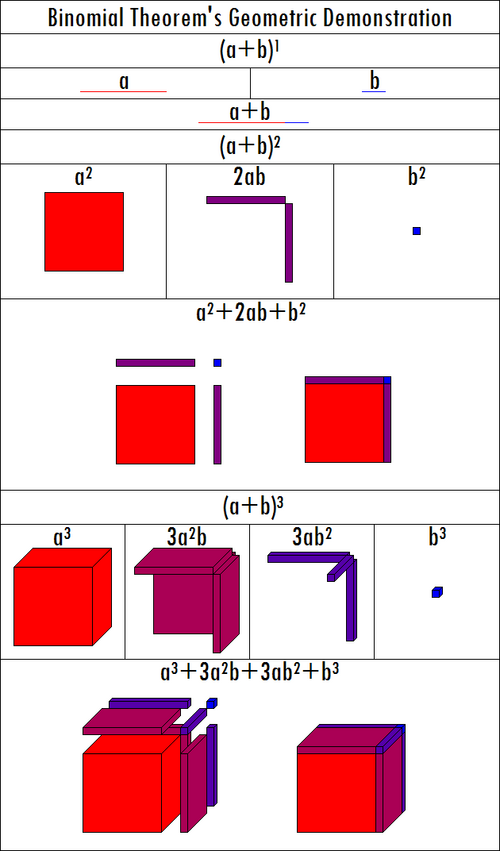
This image provides a geometric visualization of the binomial theorem, showing how expressions like (a+b)ⁿ expand into structured area components. It demonstrates why expansions naturally produce multiple x–h terms. The geometric interpretation exceeds syllabus requirements but supports conceptual intuition. Source.

$(x+h)^n = x^n + n x^{\,n-1} h + \text{higher-order terms in } h$

$n$ = Positive integer exponent

This expansion highlights why differentiation of power functions consistently produces a factor of $n$ multiplied by a reduced exponent. Higher-order terms include powers of $h$ that vanish in the limit, leaving only the linear term in $h$ relevant to the derivative.

A key takeaway is that the limit process naturally filters out all nonlinear $h$ terms, revealing the rate of change encoded in the function’s algebraic structure.

Executing the Limit Process

After substitution and expansion, the next step is to analyze how the expression simplifies once divided by $h$ . This division prepares the expression for taking the limit as $h$ approaches zero. The simplification step demonstrates that only the coefficient of the first-degree term in $h$ contributes to the derivative.

Why Higher-Order Terms Disappear

Each term involving $h^2$ , $h^3$ , and so on becomes negligible as $h \to 0$ . Since these terms still contain a factor of $h$ after dividing by $h$ , they shrink to zero, leaving only one dominant term. This behavior motivates and justifies the structure of the power rule, linking the algebraic form of the function to its instantaneous rate of change.

$f'(x) = \lim_{h\to 0}\dfrac{(x+h)^n - x^n}{h} = n x^{\,n-1}$

$f'(x)$ = Derivative of the power function

By seeing the derivative emerge directly from the limit definition, students understand not only the rule but also the reasoning behind it.

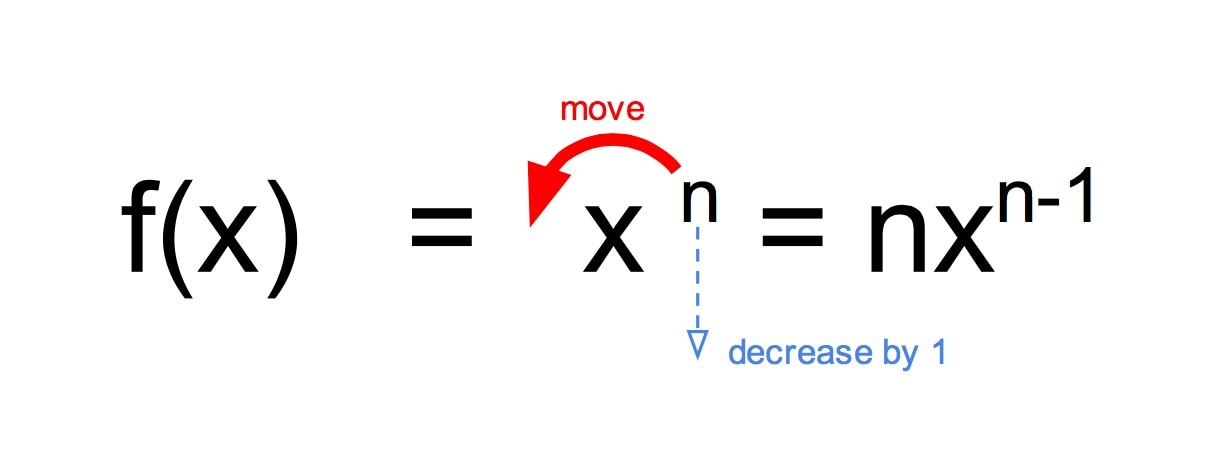
This compact visual summarizes the power rule, illustrating how the exponent becomes the new coefficient and then decreases by one. It reinforces the symbolic pattern derived from first principles. The image serves as a concise mnemonic aligned with the final expression f′(x) = nxⁿ⁻¹. Source.

Motivating the General Power Rule

The structure of the derivation reveals two important insights that justify the general power rule:

- The exponent decreases by one because subtracting $x^n$ from the expansion and dividing by $h$ isolates the term involving $x^{\,n-1}$ .

- The original exponent appears as a coefficient because the expansion of $(x+h)^n$ contains $n$ copies of the $x^{\,n-1}h$ term, demonstrating why the derivative of $x^n$ is $n x^{\,n-1}$ .

Conceptual Significance

This derivation supports deeper understanding beyond symbolic manipulation. It shows that the power rule is not arbitrary; it arises from:

- The algebraic structure of power functions.

- The limiting process that defines instantaneous change.

- The predictable pattern created by binomial expansion.

FAQ

When substituting x + h into a power function, the binomial expansion reveals how each term in the expression depends on h. Only the term containing h to the first power ultimately contributes to the derivative; all higher-power terms vanish in the limit.

This structure explains why the coefficient n and the reduced exponent n − 1 naturally appear in the power rule.

Yes, but it requires algebraic manipulation before applying the limit definition. For example, x⁻ⁿ must be rewritten as 1 divided by xⁿ so that the difference quotient can be simplified meaningfully.

The resulting derivative still follows the same pattern: the exponent becomes the coefficient, and the new exponent decreases by one.

The strength of the first-principles derivation lies in its generality. Once shown for xⁿ, the rule applies to each term in any polynomial because polynomial functions are sums of individual power terms.

The linearity of limits and differentiation allows each term to be differentiated independently and then recombined.

Terms with h², h³, or higher shrink much faster than the linear h term as h approaches zero. After dividing the expanded expression by h, higher-power terms still contain at least one factor of h.

Since these terms vanish in the limit, only the first-degree term determines the derivative.

Working from the definition shows how instantaneous rate of change emerges from the structure of the function itself, rather than appearing as an arbitrary rule.

It also reveals the algebraic mechanism behind differentiation, making it easier to understand and trust more advanced rules built from this foundation.

Practice Questions

Question 1 (1–3 marks)
The derivative of a function f is defined using first principles.
Given f(x) = x³, use the limit definition of the derivative to state the expression that must be evaluated in order to compute f′(x) from first principles.
Do not simplify the expression.

Question 1 (1–3 marks)
• 1 mark: Writes the correct difference quotient for f(x) = x³:
[f(x + h) − f(x)] / h
• 1 mark: Substitutes correctly to obtain [(x + h)³ − x³] / h
• 1 mark: Includes the limit notation needed for first principles:
lim as h → 0 [(x + h)³ − x³] / h

Maximum: 3 marks

Question 2 (4–6 marks)
A function g is defined by g(x) = x⁴.
(a) Starting from the limit definition of the derivative, derive g′(x).
(b) Explain briefly why, in the limit process, all terms involving powers of h greater than 1 vanish as h approaches 0.
(c) State the general pattern for the derivative of xⁿ for positive integers n, based on your derivation.

Question 2 (4–6 marks)

(a) Deriving g′(x) (3 marks)
• 1 mark: Writes the correct first-principles setup:
lim as h → 0 [g(x + h) − g(x)] / h
• 1 mark: Correctly expands (x + h)⁴ or outlines its required expansion.
• 1 mark: Simplifies appropriately to obtain g′(x) = 4x³

(b) Explanation of higher-order h terms (1–2 marks)
• 1 mark: States that each higher-order term still contains at least h² after dividing by h.
• 1 mark: Explains that these terms tend to 0 as h approaches 0.

Maximum: 6 marks

Try All Topic Practice Questions

Written by:

Dr Rahil Sachak-Patwa

Oxford University - PhD Mathematics

Rahil spent ten years working as private tutor, teaching students for GCSEs, A-Levels, and university admissions. During his PhD he published papers on modelling infectious disease epidemics and was a tutor to undergraduate and masters students for mathematics courses.