Sum and Difference Rules for Derivatives (2.6.2) | AP Calculus AB Notes

AP Syllabus focus:
‘Differentiate sums and differences of differentiable functions by taking derivatives term by term, using f(x) ± g(x) → f′(x) ± g′(x) to simplify calculations.’

The sum and difference rules allow derivatives to be computed efficiently by treating each component function separately, streamlining differentiation and supporting deeper understanding of functional behavior.

Understanding the Purpose of Sum and Difference Rules

These rules provide a foundational method for differentiating expressions built from multiple functions. Rather than returning to the limit definition for every term, students use these rules to differentiate term by term, reinforcing the idea that differentiation operates locally on each part of an expression. This approach greatly reduces computational complexity and prepares students for more advanced rules introduced later in the course.

The Structure of Sums and Differences in Functions

A function expressed as a sum or difference, such as $f(x) + g(x)$ or $f(x) - g(x)$ , combines the behavior of its component functions. Because derivatives measure instantaneous change, the derivative of a combined function depends on how each individual part changes. This motivates why the derivative of a sum is the sum of the derivatives, and likewise for differences, provided all component functions are differentiable.

Differentiability and Its Role in These Rules

Before applying these rules, students must ensure that each component function is differentiable on the interval of interest. A function is differentiable at a point if its derivative exists at that point.

Differentiable Function: A function is differentiable at a point if its derivative exists there, meaning the instantaneous rate of change is well defined.

Formal Statement of the Sum and Difference Rules

Although the rules appear intuitive, they stem from the linearity of the derivative operator. When applied correctly, they reinforce the conceptual link between average rates of change, instantaneous rates, and functional behavior.

$\text{Sum Rule: } (f(x) + g(x))' = f'(x) + g'(x)$
$f(x)$ , $g(x)$ = Differentiable functions
$f'(x)$ , $g'(x)$ = Their derivatives

$\text{Difference Rule: } (f(x) - g(x))' = f'(x) - g'(x)$
Variables as above

Because differentiation respects addition and subtraction, students may apply the rules without rederiving them each time.

These equations highlight the operational simplicity of the rules: when differentiating long expressions, each term may be processed individually and reassembled.

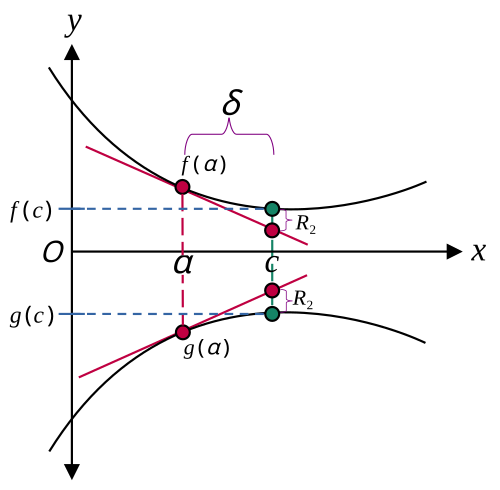
Graphical representation of tangent line approximation for two functions fff and ggg at the same input value. Each tangent line’s slope corresponds to the derivative of its function at that point, reinforcing that derivatives are computed per function. This also foreshadows how, under the sum and difference rules, the derivative of a combined function is built by adding or subtracting these individual slopes, even though the image itself does not show f±gf \pm gf±g explicitly. Source.

Why These Rules Matter in AP Calculus AB

The sum and difference rules are essential not only for symbolic calculations but also for interpreting real-world contexts. Many applied models combine functions representing different influences on a system. Being able to differentiate each part separately allows students to analyze how individual components contribute to total rates of change.

For example, if a quantity depends on multiple additive factors, the instantaneous rate of change of the total is the combined rate of change of its parts. This aligns with the syllabus requirement to “differentiate sums and differences of differentiable functions by taking derivatives term by term,” emphasizing both procedural fluency and conceptual clarity.

Key Features of the Rules

1. Linearity of Differentiation

The derivative operator behaves linearly under addition and subtraction. This linearity is one of the earliest structural properties students encounter in calculus and serves as a stepping stone to later rules involving products, quotients, and compositions.

2. No Additional Conditions Beyond Differentiability

Only one condition is necessary: the involved functions must be differentiable. Unlike some later rules that impose domain constraints (e.g., logarithmic derivatives), the sum and difference rules apply broadly.

3. Simplification Before Differentiation

In many expressions, especially polynomial or algebraic ones, simplifying the function before differentiating often reveals terms more easily handled with these rules. This strengthens algebraic reasoning alongside calculus skills.

4. Term-by-Term Interpretation

Students should internalize that each part of a function contributes individually to the overall rate of change. This perspective encourages deeper graphical and contextual reasoning, such as recognizing that increasing or decreasing trends in separate components combine predictably.

Practical Application Strategies

To apply these rules effectively, students should follow a consistent process:

Identify each term in the sum or difference.
Confirm differentiability of each component on the interval.
Differentiate each term individually using the appropriate rule (power rule, exponential rule, trigonometric derivatives, etc.).
Reassemble the differentiated terms, maintaining the original addition or subtraction structure.
Simplify if needed to express the derivative more clearly.

Developing fluency with this process prepares students to handle polynomial functions, trigonometric expressions, exponential models, and hybrid forms that frequently appear in AP-level problems.

Conceptual Interpretation of the Rules

Beyond procedural skill, students must interpret derivatives of combined functions meaningfully. The derivative of a sum represents the combined instantaneous contributions of its parts. The derivative of a difference reveals how competing processes influence overall change. These interpretations align closely with AP Calculus AB’s emphasis on understanding derivatives as instantaneous rates and using them to describe real-world relationships.

Integration with Later Topics

This subsubtopic serves as a foundation for subsequent derivative rules. Efficient handling of sums and differences allows students to focus on more complex operations like products, quotients, and compositions without being slowed by unnecessary re-evaluation of basic symbolic steps. Mastery here strengthens overall confidence and computational agility across the entire differentiation unit.

(1)

where denotes a derivative and and are the derivatives of and , respectively.

Given real-valued functions and that are continuous on the closed interval , sum rule for definite integration states,

(2)

Similarly, the sum rule for indefinite integration states,

Formal statement of the sum rule for derivatives: the derivative of a sum equals the sum of the derivatives. This compact formula visually reinforces the rule you state in the notes, (f±g)′(x)=f′(x)±g′(x)(f \pm g)'(x) = f'(x) \pm g'(x)(f±g)′(x)=f′(x)±g′(x). The page also includes sum rules for integrals, which extend beyond this subsubtopic but do not affect the correctness of this derivative-focused formula. Source.

FAQ

Use these rules whenever the expression is a straightforward addition or subtraction of functions without multiplication or composition. If no variables are being multiplied together or substituted into another function, the sum and difference rules are usually the correct choice.

A useful check is to rewrite the expression in its simplest algebraic form. If it becomes a list of separate terms, each depending on x, then differentiate term by term.

Yes. The order of terms does not affect differentiability or the operation of the rules. Differentiation respects both addition and subtraction regardless of arrangement.

However, placing terms in a consistent order can help avoid sign errors. Many students find it easier to group positive and negative terms before differentiating.

First check whether the original function could be simplified. Algebraic manipulation often shortens the derivative significantly.

Then check for common errors:
• missed negative signs
• incorrect power reductions
• forgetting to apply the rule to every term

A final check is to mentally estimate whether each term is increasing or decreasing to see if the sign of its derivative makes sense.

A constant term has no change as x changes, so its derivative is zero. When applying the sum and difference rules, this simply means the constant contributes nothing to the final derivative.

This is why, in expressions mixing constants and variable terms, only the parts involving x generate non-zero derivatives.

Yes, but only within intervals where all component functions are differentiable. At boundaries where a piecewise function changes formula, the derivative may fail to exist.

To apply the rules safely:
• differentiate each piece separately
• ensure the pieces join with matching left- and right-hand derivatives if a derivative at the boundary is required

Practice Questions

Question 1 (1–3 marks)
A function is defined by H(x) = 7x³ − 4x + 5x².
(a) Use the sum and difference rules to find H′(x).
(b) Hence, state the value of H′(2).

Question 1
(a) 2 marks
• 1 mark for correctly differentiating each term:
d/dx(7x³) = 21x², d/dx(−4x) = −4, d/dx(5x²) = 10x.
• 1 mark for the correct combined answer:
H′(x) = 21x² + 10x − 4.

(b) 1 mark
• Substitution into the derivative: H′(2) = 21(4) + 10(2) − 4 = 84 + 20 − 4 = 100.

Total: 3 marks

Question 2 (4–6 marks)
Let p(x) = 3f(x) − 2g(x), where f and g are differentiable functions.
You are given the following values:
f(1) = 4, f′(1) = −3
g(1) = 2, g′(1) = 5

(a) Use the sum and difference rules to write an expression for p′(x) in terms of f′(x) and g′(x).
(b) Hence calculate p′(1).
(c) Briefly explain, in words, why it is valid to differentiate p(x) term by term.

Question 2
(a) 2 marks
• 1 mark for applying the constant multiple rule correctly.
• 1 mark for applying the sum and difference rules correctly:
p′(x) = 3f′(x) − 2g′(x).

(b) 2 marks
• 1 mark for correct substitution of values: 3f′(1) = 3(−3) = −9 and −2g′(1) = −2(5) = −10.
• 1 mark for the final value: p′(1) = −9 − 10 = −19.

(c) 1–2 marks
• 1 mark for stating that f and g are differentiable functions.
• 1 mark for explaining that differentiability ensures each term’s derivative exists, allowing the derivative of the whole expression to be found by differentiating each part separately.

Total: 5–6 marks

Try All Topic Practice Questions

Written by:

Dr Rahil Sachak-Patwa

Oxford University - PhD Mathematics

Rahil spent ten years working as private tutor, teaching students for GCSEs, A-Levels, and university admissions. During his PhD he published papers on modelling infectious disease epidemics and was a tutor to undergraduate and masters students for mathematics courses.