AP Syllabus focus:
‘Differentiate f to obtain f′, then differentiate again to find the second derivative f″, provided each derivative exists, reinforcing that higher-order derivatives repeat familiar rules.’
Understanding how to move from a first derivative to a second derivative is essential for analyzing a function’s changing behavior, especially its curvature, motion characteristics, and overall graphical structure.
From First to Second Derivative
The process of obtaining the second derivative begins by differentiating a given function to find its first derivative, then differentiating once more. This sequential differentiation reinforces that familiar rules—such as the power rule, product rule, quotient rule, and chain rule—apply repeatedly whenever higher-order derivatives are required. The second derivative provides information about how the first derivative changes, preparing students for deeper analysis in later topics.
Understanding Higher-Order Differentiation
A higher-order derivative is any derivative taken after the first. The second derivative specifically measures how quickly the first derivative changes with respect to the independent variable. Whenever the first derivative exists and is differentiable, the second derivative is defined.
Second Derivative: The derivative of the first derivative of a function, describing the rate of change of the rate of change.
Before differentiating again, it is crucial to ensure that the first derivative is properly simplified, clearly written, and differentiable over the interval of interest. This prevents unnecessary complexity when applying familiar rules a second time.
A brief symbolic expression is often used in calculus to represent this repeated differentiation.
= the second derivative
= the first derivative
The notation helps students keep track of derivative order while recognizing that no new differentiation rules are required beyond those already mastered.
A sentence here ensures proper spacing before the next special formatting block.
Order of a Derivative: A number indicating how many times a function has been differentiated, with first, second, and third derivatives being the most common.
Graphically, you can think of three related curves: one for the original function, one for its slope f′f′f′, and one for how that slope is changing, f″f″f″.
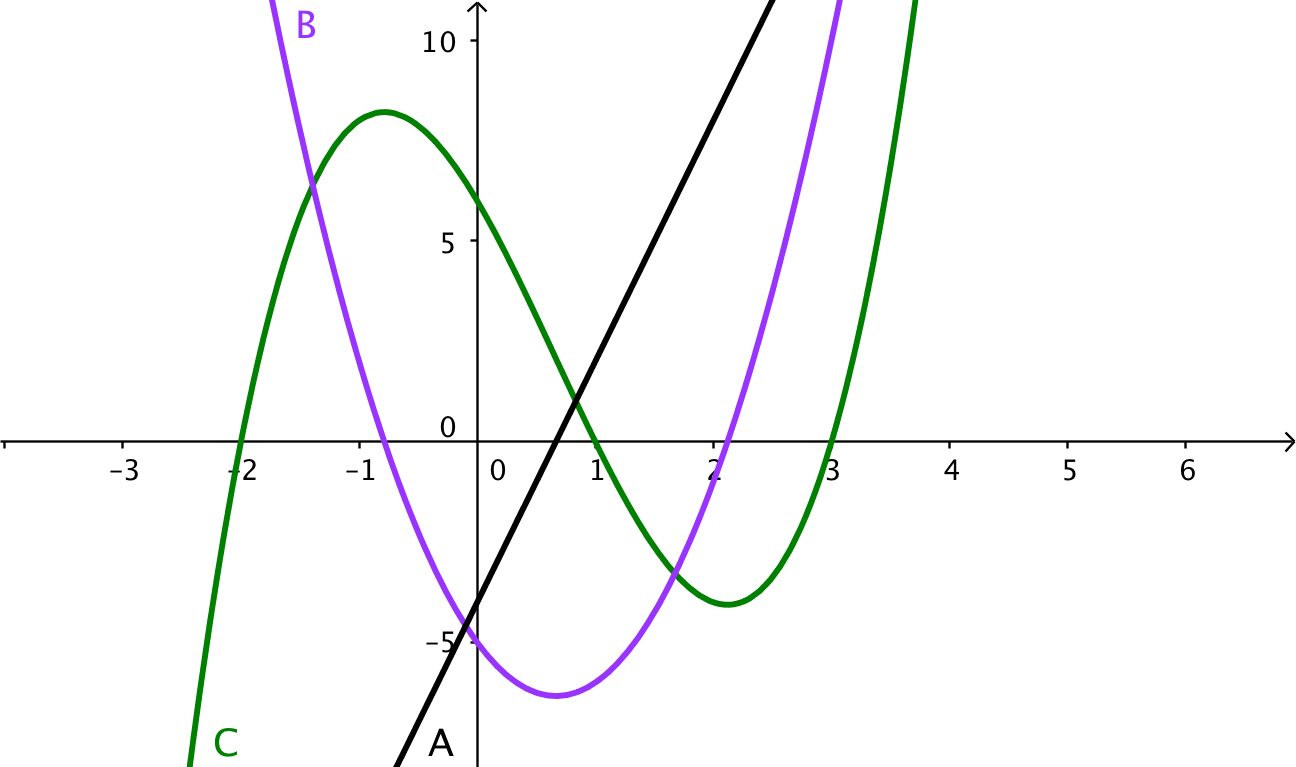
This graph shows a function fff (green), its first derivative f′(x)f'(x)f′(x) (purple), and its second derivative f′′(x)f''(x)f′′(x) (black) plotted together. Notice how local maxima and minima of fff occur where f′(x)=0f'(x) = 0f′(x)=0, and how changes in concavity correspond to sign changes of f′′f''f′′. The image includes curve labels, providing slightly more detail than required while effectively illustrating the relationship between the derivatives. Source.
Why the Process Matters
Differentiating twice reveals deeper structural information about a function. Whereas the first derivative describes slope and instantaneous rate of change, the second derivative describes how that slope changes. This information is foundational for later study of concavity, inflection points, and physical interpretations such as acceleration in motion problems.
Students should become comfortable interpreting second derivatives because they form a bridge between computational techniques and conceptual understanding of function behavior.
General Procedure for Finding the Second Derivative
Although each function may require a different combination of derivative rules, the overall procedure remains consistent.
To compute a second derivative:
Differentiate the original function once to obtain f′(x).
Simplify f′(x) algebraically so the next step is clear.
Differentiate f′(x) again to obtain f″(x).
Apply the power, product, quotient, or chain rule whenever the expression requires it.
Verify that each step is valid by ensuring differentiability where needed.
Higher-order differentiation is simply an extension of familiar skills, but accuracy becomes increasingly important, especially when expressions involve multiple operations.
Applying Familiar Rules More Than Once
Repeated differentiation often requires applying known derivative rules multiple times. Students should expect the following scenarios:
Power rule applications when exponents persist after the first differentiation.
Product or quotient rule repetitions if the structure of the original problem carries through to the first derivative.
Chain rule involvement whenever a composite function remains after the first differentiation.
Constant multiples remaining unaffected by repeated differentiation.
Terms disappearing once differentiated enough times, particularly in polynomial functions.
The iterative nature of this process helps students recognize patterns, especially when functions simplify dramatically after successive differentiation.
Structural Importance of the Second Derivative
Beyond computation, the second derivative plays a critical structural role in calculus. It helps determine:
How a curve bends or curves upward or downward.
How rapidly rates of change evolve in real-world models.
How functions behave locally, which is essential for curve sketching.
Whether certain features such as inflection points may exist, though full analysis occurs in later subtopics.
These interpretations rely on mastery of the process of moving from the first to the second derivative, reinforcing the central idea that repeated differentiation involves no new rules, only deeper application of existing ones.
For example, if f(x)f(x)f(x) is a smooth curve like a parabola, then f′(x)f′(x)f′(x) gives the slope of that curve at each point, and f″(x)f″(x)f″(x) measures how that slope itself is changing.
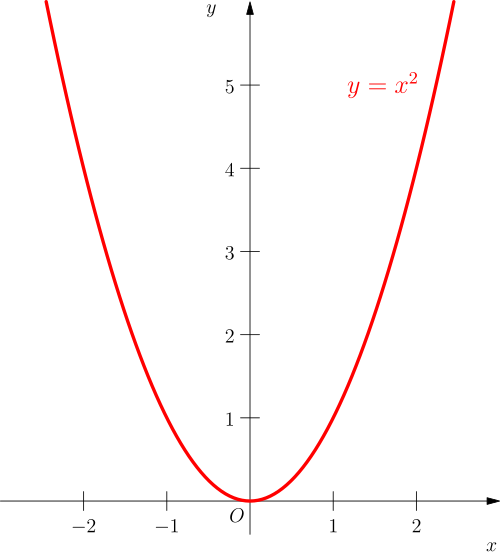
This figure shows the graph of the parabola y=x2y = x^2y=x2, a standard example illustrating repeated differentiation. For this function, f′(x)=2xf'(x) = 2xf′(x)=2x is linear and f′′(x)=2f''(x) = 2f′′(x)=2 is constant, reflecting steadily increasing slope. Although the image does not depict f′(x)f'(x)f′(x) or f′′(x)f''(x)f′′(x), it provides a clear geometric basis for understanding how successive derivatives relate to the shape of a function. Source.
Notational Clarity
Multiple notations exist for second derivatives, each serving a different purpose in calculus. Understanding them helps students read problems accurately and communicate solutions effectively.
= alternative shorthand notation
Students should become comfortable switching between notation systems depending on context, whether analyzing functions, solving differential equations later, or interpreting derivatives from graphs or tables.
Building Toward Advanced Concepts
The skill of differentiating twice prepares students for deeper conceptual ideas without adding mechanical complexity. Since higher-order derivatives simply repeat the familiar process of differentiation, confidence with the transition from f′ to f″ ensures readiness for analysis involving concavity, optimization structures, and motion interpretation in subsequent study.
FAQ
For a second derivative to exist at a point, the first derivative must exist in a neighbourhood of that point and be differentiable there.
This means the function must be sufficiently smooth, with no sharp corners, cusps, or vertical tangents that would prevent the slope from changing smoothly.
Continuity of the first derivative is usually a good indicator, though it is not strictly required in every case.
Yes, this is possible.
A function may have a well-defined slope at every point, but the slope itself may change abruptly at certain points, preventing the second derivative from existing there.
This typically occurs when the graph of the first derivative has a sharp corner or cusp.
Repeated differentiation can reduce the complexity of a function, especially for polynomials.
Each differentiation lowers the degree of a polynomial, eventually producing a constant or zero.
This simplification helps reveal patterns in how rates of change evolve and makes it easier to interpret long-term behaviour of functions.
If the second derivative is zero over an interval, the first derivative is constant, meaning the rate of change does not vary.
If the second derivative is non-zero, the rate of change is itself changing.
The size of the second derivative indicates how rapidly the slope is increasing or decreasing.
Yes, but only at isolated points.
At a single point, a second derivative of zero indicates that the slope is not changing at that instant.
However, for a function to be linear over an interval, the second derivative must be zero throughout that entire interval.
Practice Questions
Question 1 (2 marks)
A function f is differentiable for all real x and has first derivative
f′(x) = 6x − 4.
(a) Find the second derivative of f.
(b) State one conclusion about how the slope of f changes for increasing x.
Question 1
(a)
Correct differentiation of f′(x) to obtain f″(x) = 6 (1 mark)
(b)
Correct statement that the slope of f increases at a constant rate, or that the slope is increasing because the second derivative is positive (1 mark)
Question 2 (5 marks)
A particle moves along a straight line and its position at time t seconds is given by a differentiable function s(t).
The velocity of the particle is given by
v(t) = 3t² − 12t + 5.
(a) Find the acceleration of the particle at time t.
(b) Find the time(s) when the acceleration is zero.
(c) Describe what the sign of the acceleration tells you about how the velocity is changing for t > 4.
Question 2
(a)
Correct differentiation of v(t) to obtain acceleration a(t) = 6t − 12 (2 marks)
(b)
Correct equation set up: 6t − 12 = 0 (1 mark)
Correct solution t = 2 (1 mark)
(c)
Correct interpretation that for t > 4 the acceleration is positive, so the velocity is increasing (1 mark)

