AP Syllabus focus:
‘Apply the chain rule, product rule, or quotient rule repeatedly to compute higher-order derivatives for composite functions, using clear notation to track each differentiation.’
Higher-order derivatives of composite functions require systematic reuse of the chain rule, often combined with the product or quotient rule, to maintain clarity, accuracy, and efficient symbolic organization.
Higher-Order Derivatives Using the Chain Rule
Higher-order derivatives describe how earlier derivatives change and often arise when differentiating composite functions multiple times. Because each differentiation exposes additional structure inside a composition, repeated use of the chain rule is essential. When a composite expression also involves multiplication or division, the product rule or quotient rule must be integrated into the process. Developing a clear, stepwise strategy prevents errors and ensures accurate results.
Understanding Repeated Differentiation in Composites
When a function is built from nested components, each derivative reveals further layers of dependence on the inner function and its derivatives. The repeated presence of the inside function means the chain rule remains active at every stage. Higher-order derivatives can therefore expand quickly, and well-organized notation helps track each resulting term.
Higher-Order Derivative: The result of differentiating a function more than once, such as the second derivative f''(x) or the nth derivative f^(n)(x).
A higher-order derivative of a composite such as y = f(g(x)) is obtained by applying the chain rule repeatedly to the nesting of the functions.
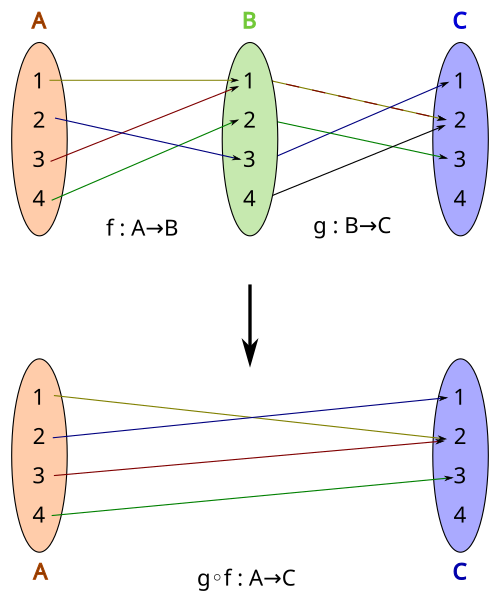
This arrow diagram shows a composite function g∘f built from two mappings f: A → B and g: B → C. It highlights how inputs move through the inner and then outer function, mirroring the layered differentiation structure in the chain rule. Students can connect the arrows to repeated differentiation steps in higher-order derivatives of composites. Source.
Between successive derivatives, the outer structure of the expression may change significantly, especially if differentiation introduces new products. This shift often increases the number of rules required at later stages.
Applying the Chain Rule Repeatedly
Each application of the chain rule differentiates an outer function while multiplying by the derivative of the inner function. When higher-order derivatives are computed, the inner function may be differentiated multiple times, generating additional layers of terms.
Chain Rule (First Derivative) = f′(g(x)) · g′(x)
f′(g(x)) = Derivative of the outer function evaluated at the inner function
g′(x) = Derivative of the inner function
For the first derivative of a composite, the chain rule gives dy/dx = f′(g(x)) · g′(x), and higher-order derivatives keep reusing this structure.
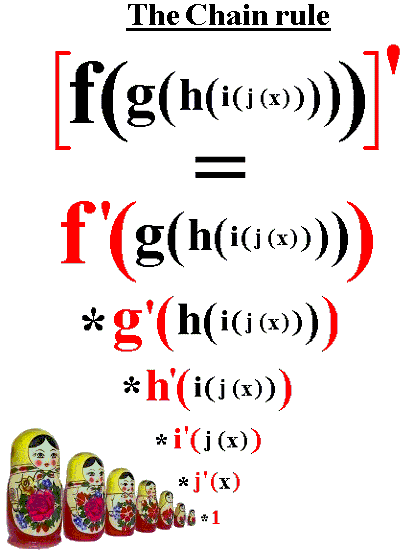
This formula panel summarizes the chain rule in multiple notations, including dy/dx = (dy/du)(du/dx) and (f∘g)'(x) = f'(g(x))g'(x). It reinforces that differentiating a composite multiplies the derivative of the outer function by the derivative of the inner function. This structural pattern underlies higher-order derivatives as the rule is applied repeatedly. Source.
A second differentiation requires differentiating both factors that appear in the first derivative, naturally invoking additional rule combinations. This process continues for third and higher derivatives whenever needed.
Coordinating the Chain Rule with Product and Quotient Rules
Because repeated differentiation of a composite almost always produces products, the chain rule quickly intertwines with the product rule. The structure may become increasingly algebraic, so recognizing these patterns early is essential. Students should prioritize symbolic clarity and track dependencies carefully.
Product Rule: A rule stating that the derivative of u(x)v(x) is u′(x)v(x) + u(x)v′(x).
A normal sentence ensures smooth continuity before the next block.
Quotient Rule: A rule stating that the derivative of u(x)/v(x) is (u′(x)v(x) − u(x)v′(x)) / (v(x))².
When these rules are combined repeatedly with the chain rule, each term must be handled separately. Failing to maintain consistent notation can obscure relationships among terms, particularly in higher-order derivatives.
Notational Strategies for Tracking Multiple Differentiations
Accurate organization is crucial when differentiating composites multiple times. Students should adopt consistent use of prime notation, Leibniz notation, or functional notation. Each system offers advantages depending on the structure of the function and the complexity of the derivative.
Key practices for clarity include:
Clearly labeling derivatives of inner and outer functions (for example, g'(x), g''(x)).
Maintaining parentheses around composite expressions to avoid misinterpretation.
Marking each differentiation step explicitly when multiple rules are used together.
Using indentation or line breaks when writing expansions involving many terms.
Tracking where each derivative originated so terms are not lost during simplification.
Planning the Differentiation Sequence
Before computing a higher-order derivative, it is beneficial to analyze the structure of the function to determine which rules will eventually become necessary. Composite functions often evolve into products after one differentiation, and products may become quotients depending on algebraic manipulation. Anticipating these changes improves efficiency and reduces rewriting later.
A strategic approach includes:
Identifying the outermost function whose derivative will appear first.
Identifying all inner functions and their derivatives that will appear repeatedly.
Predicting whether new product or quotient structures will develop after the first derivative.
Maintaining clear notation for every new term generated.
Why Repeated Use of the Chain Rule Matters
Higher-order derivatives provide important information about curvature, motion, and the behavior of models involving nested functional relationships. The chain rule ensures these derivatives correctly capture how inner functions influence outer ones at each stage of differentiation. When combined with product and quotient rules where appropriate, the chain rule produces complete expressions that reflect the layered structure of the original function.
Each time we differentiate again, the new derivative measures how the previous derivative is changing, so the second derivative describes how the slope changes and is closely linked to concavity.
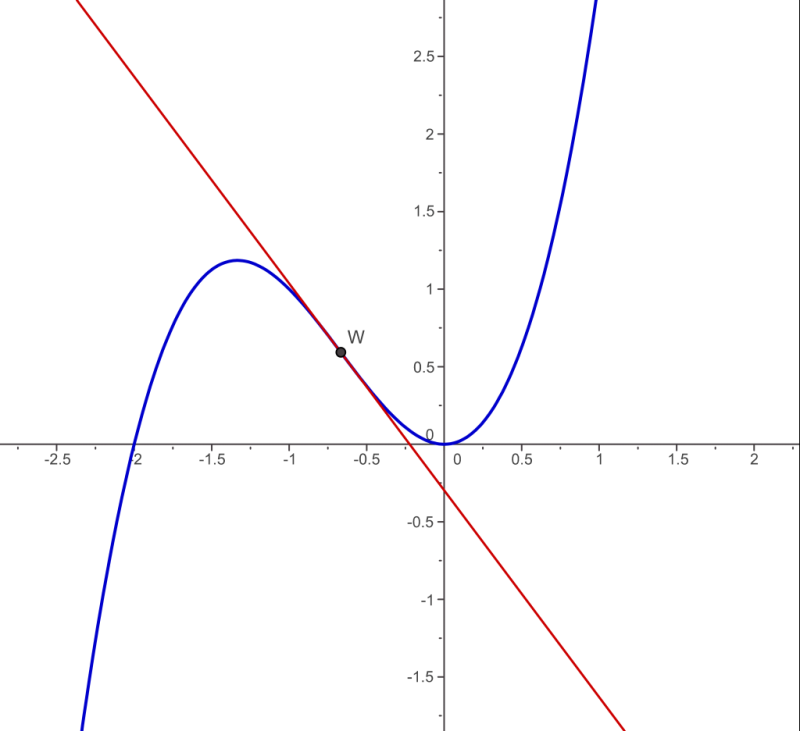
This graph shows the curve y = x³ + 2x² with an inflection point where the concavity changes sign. The behavior at this point reflects a change in the second derivative, found by differentiating the first derivative again. Although it features a specific polynomial rather than a composite function, it illustrates how higher-order derivatives describe changes in curvature. Source.
Summary of Process for Higher-Order Derivatives in Composites
Differentiate the outer function first, leaving the inside function unchanged.
Multiply by the derivative of the inside function, applying the chain rule.
Differentiate the resulting expression again, using product and quotient rules as required.
Keep notation consistent to track each function and its derivative order.
Repeat systematically until the required derivative order is reached.
FAQ
Look for functions built from nested expressions, especially where an inner function will still be present after the first differentiation.
Typical signals include:
• A composition appearing inside a product or quotient
• An inner function whose derivative is non-constant
• Expressions that become more complicated, not simpler, after one derivative
If the inner function does not disappear after differentiating once, repeated chain rule use is almost certain.
Each differentiation acts on every part of the previous derivative, and composite functions often produce products such as f’(g(x)) g’(x).
On the next differentiation, both factors must be differentiated, which triggers the product rule as well as further applications of the chain rule.
This branching effect continues with each derivative order, causing the expression to grow in length even if the original function is compact.
A structured layout prevents terms from being lost and clarifies which rule applies at each step.
Useful strategies include:
• Writing the derivative order (first, second, third) clearly before each line
• Indenting or spacing terms so product rule expansions remain readable
• Highlighting the inner function and its derivatives to avoid duplication
Clear layout often saves time compared with hurried algebraic manipulation.
Consider whether simplification removes or creates composite structure.
If simplification eliminates unnecessary nesting or factors that obscure the inner function, perform it first.
If simplifying would force expansion of expressions that are easier to differentiate in compact form, differentiate first.
A good rule of thumb: simplify only when it reduces the number of rule applications, not when it increases them.
The same symbols often reappear at different derivative orders, making ambiguity a genuine risk.
Precise notation ensures that:
• Derivatives of outer and inner functions are not confused
• Each chain rule multiplication is matched with the correct derivative
• Higher-order derivatives like p''(q(x)) and q''(x) are clearly distinguished
Well-kept notation reduces algebraic errors and helps track how each component contributes to the final derivative.
Practice Questions
(1–3 marks)
A function is defined by y = f(g(x)), where f and g are differentiable.
Given that g(2) = 5, g’(2) = 3, and f’(5) = −4, find y’(2).
Question 1 (3 marks total)
• Correct use of the chain rule structure y’(x) = f’(g(x)) · g’(x). (1 mark)
• Substitution of g(2) = 5 into f’(g(2)). (1 mark)
• Final numerical answer: y’(2) = f’(5) · 3 = −4 · 3 = −12. (1 mark)
(4–6 marks)
A function is defined by H(x) = x² · p(q(x)), where p and q are differentiable functions.
(a) Differentiate H(x) to obtain H’(x).
(b) Hence find H’’(x), showing clearly where the chain rule and product rule are applied.
Question 2 (6 marks total)
(a)
• Correct use of product rule on x² · p(q(x)). (1 mark)
• Correct derivative of x² giving 2x. (1 mark)
• Correct application of chain rule to p(q(x)), giving p’(q(x)) · q’(x). (1 mark)
Expression for H’(x) should be:
H’(x) = 2x p(q(x)) + x² p’(q(x)) q’(x).
(b)
• Correct differentiation of 2x p(q(x)) using product rule and chain rule. (1 mark)
• Correct differentiation of x² p’(q(x)) q’(x), applying product rule and differentiating p’(q(x)) with the chain rule. (1 mark)
• Fully simplified or clearly expressed final form of H’’(x) with all necessary terms. (1 mark)
A typical correct expression for H’’(x) (any equivalent form accepted):
H’’(x) = 2 p(q(x)) + 4x p’(q(x)) q’(x) + x² [ p’’(q(x)) (q’(x))² + p’(q(x)) q’’(x) ].

