AP Syllabus focus:
‘Understand notations for higher-order derivatives such as d²y/dx², y″, and f⁽ⁿ⁾(x), and recognize that all of them describe repeated differentiation of the same function.’
Higher-order derivative notation extends the idea of differentiation by providing systematic symbols that represent repeated derivatives, allowing students to interpret how a function’s behavior evolves across successive rates of change.
Higher-Order Derivatives in Context
Higher-order derivatives arise when a function is differentiated more than once, and their notation communicates both the order of differentiation and the underlying function being studied. In AP Calculus AB, understanding multiple notation systems is essential because different problem types—algebraic, graphical, and applied—may present derivatives using distinct symbolic forms. Despite the differences in appearance, all higher-order derivative notations share one purpose: they capture how earlier derivatives change and how the rate of change evolves with each differentiation.
Standard Function Notation for Higher-Order Derivatives
The most common notation for a higher-order derivative uses the function name directly. When a function is written as f(x), its first derivative is written as f'(x), the second derivative as f''(x), and, more generally, the nth derivative as f^(n)(x). Students should recognize that this pattern expresses repeated differentiation with efficiency and clarity, especially when the function is explicitly defined.

This diagram lists the standard prime notation for the first, second, third, fourth, and nth derivatives of a function using both y and f(x) notation. It highlights how the number of primes or the superscript (n) indicates the order of the derivative. The content matches the notation used in AP Calculus AB without adding any extended rules. Source.
Higher-Order Derivative f^(n)(x): The result of differentiating a function f repeatedly n times, assuming each derivative exists.
This notation is widely used in theoretical settings, where the order of differentiation is emphasized without reference to dependent variables such as y. It also appears frequently in polynomial and power function contexts, where discerning patterns in successive derivatives is particularly helpful.
Leibniz Notation for Higher-Order Derivatives
Another essential representation is Leibniz notation, which expresses higher-order derivatives in terms of the variables being differentiated. When a function is expressed as y = f(x), the first derivative appears as dy/dx, while the second derivative is written as d²y/dx², and the nth derivative as dⁿy/dxⁿ. This format highlights the differential relationship between x and y, making it especially valuable in problems involving implicit differentiation or when variables play a significant conceptual role.
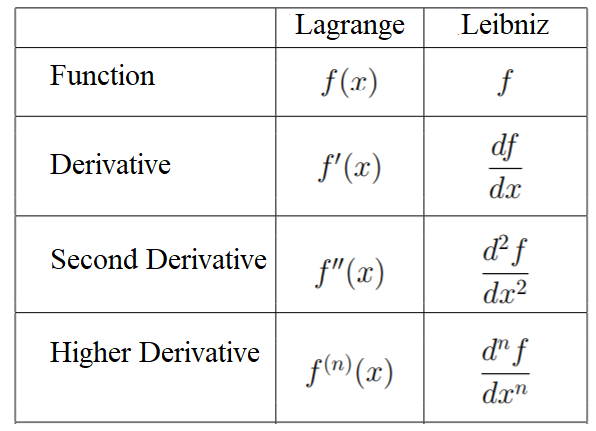
This table compares Lagrange’s prime notation f′(x), f′′(x), f^(n)(x) with the corresponding Leibniz forms dy/dx, d²y/dx², dⁿy/dxⁿ. It reinforces that these notations represent the same differentiation process using different symbolic conventions. The image also includes labels such as Function and First Derivative, which remain consistent with AP Calculus AB expectations. Source.
Second Derivative d²y/dx²: The derivative of the first derivative dy/dx with respect to x, describing how the rate of change of y itself changes.
Between the two systems, Leibniz notation is more explicit about which variable is independent, so it reinforces conceptual reasoning about slopes, curvature, and the structure of equations involving multiple variables.
Prime Notation and its Extensions
Prime notation uses apostrophes to show repeated derivatives, but it becomes cumbersome after the third derivative. The first derivative uses a single prime (y'), the second derivative uses two primes (y''), and the third derivative uses three (y'''). Beyond that point, notation typically shifts to y^(n) for clarity. Prime notation is most commonly applied when the dependent variable is written as y and when the functional relationship is straightforward enough that additional symbols are unnecessary.
Prime Notation y^(n): A compact way to express the nth derivative of y with respect to x, extending the prime system to higher orders.
While elegant, the prime system is used mainly for lower derivatives in AP Calculus AB problems, but recognizing the extension to y^(n) ensures that students can interpret more general expressions when they arise.
Relationships Among Notation Systems
Although the notations differ visually, they all represent the same mathematical idea: repeating the differentiation process. Students should become comfortable translating among them, particularly when a question switches notation mid-problem. Understanding that f''(x), y'', and d²y/dx² communicate the same second derivative helps prevent confusion and supports flexible thinking in applications involving motion, curvature, or function behavior.
Second Derivative = d²y/dx² = y'' = f''(x)
y = Dependent variable
x = Independent variable
Recognizing these equivalences ensures that notation does not become a barrier to understanding the mathematical meaning behind higher-order derivatives.
Higher-Order Derivatives and Differentiability Requirements
Before writing higher-order derivatives, it is crucial to remember that each derivative must exist for the next to be defined. This means the function must be differentiable enough times to support the order of derivative required. For instance, a second derivative exists only if the first derivative is itself differentiable. Similarly, expressing f^(n)(x) assumes the presence of all intermediate derivatives up to order n.
Why Multiple Notation Systems Matter
Different mathematical contexts favor different notations.
Function notation is concise and ideal for algebraic manipulation.
Leibniz notation is explicit and clarifies variable dependence.
Prime notation offers simplicity for early derivatives.
AP Calculus AB students benefit from mastering all forms, as exams, textbooks, graphs, and STEM fields frequently interchange them. Understanding these systems strengthens conceptual fluency and prepares students to interpret any derivative expression they encounter.
FAQ
Choose notation based on clarity and the structure of the expression.
• Use prime notation when the function is written simply as y or f and only low-order derivatives appear.
• Use Leibniz notation when variables must be shown explicitly, such as in expressions involving dy/dx or when differentiating implicitly.
• Use f^(n)(x) when discussing general derivative order or when the nth derivative appears without explicit variable dependence.
The goal is always readability and reducing ambiguity.
The exponent on the numerator indicates that the second derivative applies to y, while the exponent on the denominator reflects that differentiation is taken twice with respect to x.
This notation emphasises the repeated action of differentiating with respect to x, not exponentiation.
It provides a structural reminder that dy/dx is differentiated again with respect to x.
Yes. A function may be differentiable at all points but have a first derivative that fails to be differentiable somewhere.
This usually occurs at corners, cusps, or points where the slope changes abruptly.
Such cases show that the existence of dy/dx does not guarantee the existence of d^2y/dx^2.
Consistent notation allows you to track the order of differentiation and recognise emerging patterns.
• In polynomial functions, higher-order derivatives reduce degree in predictable steps.
• In trigonometric or exponential functions, notation helps signal when patterns become cyclical or stabilise.
Using f^(n)(x) is particularly effective when generalising patterns across multiple derivative orders.
Prime notation becomes unwieldy beyond the third derivative, making reading and transcription error-prone.
f^(n)(x) conveys order clearly, supports general statements, and avoids long chains of apostrophes.
It is also compatible with proofs, tables, and contexts where n varies, providing a flexible and universal notation system.
Practice Questions
(1–3 marks)
A function is defined by y = f(x). Write the second derivative of y with respect to x using:
(a) Leibniz notation
(b) prime notation
(a) Correct expression d^2y/dx^2. (1 mark)
(b) Correct expression y''. (1 mark)
Both correct: full 2 marks. One correct: 1 mark.
(4–6 marks)
A function g is differentiable for all real numbers, and its derivatives are given by:
g'(x) = 3x^2 − 4x
g''(x) = 6x − 4
(a) State the meaning of the notation g''(x).
(b) Write the third derivative using both function notation and Leibniz notation.
(c) Explain briefly why the derivative g^(n)(x) is defined only when all previous derivatives up to order n − 1 exist.
(a) States that g''(x) represents the derivative of g'(x) or the second derivative of g. (1 mark)
(b) Writes g'''(x). (1 mark)
Writes d^3g/dx^3. (1 mark)
(c) States that each derivative requires the previous one to exist or that repeated differentiation is only possible if earlier derivatives are defined. (1–2 marks depending on clarity)
Total: 4–6 marks depending on level of detail.

