AP Syllabus focus:
‘Follow a systematic process: draw a diagram, write an equation relating variables, differentiate implicitly with respect to time, substitute known values, and solve for the desired rate.’
A related rates problem requires a structured method so changing quantities can be connected clearly and solved efficiently, ensuring every derivative represents a meaningful rate with respect to time.
Step-by-Step Method for Solving Related Rates Problems
Understanding the Purpose of a Systematic Process
A related rates problem involves two or more quantities whose rates of change are linked. To maintain clarity, the procedure must be systematic so that each mathematical step reflects the physical or contextual situation accurately. Students often encounter difficulties when variables, units, or derivatives are mixed without organization, so a dependable framework ensures correctness and interpretability.
Step 1: Draw and Label a Diagram
A diagram clarifies spatial or quantitative relationships before any calculus is used.
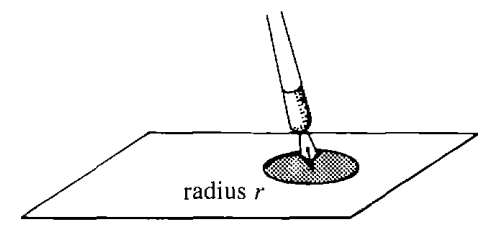
This figure shows an expanding circular ink blot whose area and radius both depend on time. The radius rrr and area AAA are labeled, illustrating how to assign variables before writing equations. Although the diagram comes from a specific example, it serves generally as a model for drawing and labeling diagrams in any related rates problem. Source.
Even a simple sketch can reveal how variables depend on one another and which parts of a situation are fixed or changing. When multiple variables appear, visual structure often determines the correct equation linking them.
Step 2: Identify and Label All Variables
Introduce each variable with a clear description. A variable is any symbol representing a quantity that may change over time or with respect to another measurement. At this stage, determine which quantities are constant, which are changing, and which rate you must ultimately compute.
Variable: A symbol representing a quantity that can change with respect to time or another variable.
When labeling variables, be consistent so derivatives can be interpreted without confusion.
Step 3: List Given Rates and the Desired Rate
A rate is the derivative of a quantity with respect to time, expressing how rapidly that quantity changes at a specific instant. State each known or unknown rate using proper notation such as or . This step ensures all information is accounted for before writing an equation.
Rate of Change: The derivative of a quantity with respect to time, indicating its instantaneous change per unit time.
One sentence here reinforces how these rates guide the differentiation step that follows.
Step 4: Write an Equation Relating the Variables
Use geometric, physical, or contextual relationships to connect the variables.
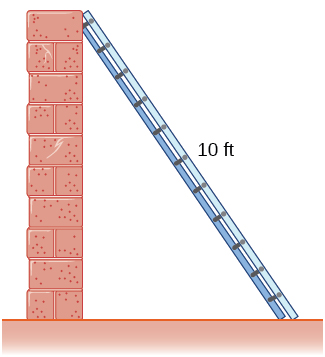
This figure shows a 10-ft ladder leaning against a wall, forming a right triangle with horizontal distance xxx and vertical height yyy. The diagram models two changing quantities whose rates will be related using the Pythagorean theorem before differentiating with respect to time. Numerical values in the diagram belong to a specific example but illustrate the general method for organizing a ladder-type related rates problem. Source.
The equation must be written before substituting numerical values, since related rates problems rely on differentiating relationships among variables, not isolated numbers. Only one equation is typically required, but it must capture all relevant dependencies.
Step 5: Differentiate Implicitly with Respect to Time
Every differentiation step must reference time because the goal is to connect how quantities change over time. This ensures that even variables not explicitly written as functions of time are treated as such during differentiation.
= A variable depending on time (units vary with context)
= Rate of change of the variable with respect to time (unit per time)
Implicit differentiation guarantees each derivative emerges as a rate linked to time-dependent behavior.
Step 6: Substitute Known Numerical Values
After differentiation, substitute all given quantities and rates corresponding to the instant described in the problem. This step should occur only after differentiation so the structure of the relationship between variables remains intact. Careful substitution maintains consistency in units and ensures the resulting expression reflects the specific moment of interest.
Step 7: Solve Algebraically for the Desired Rate
Once the equation includes only one unknown rate, solve for it. The resulting value represents the instantaneous rate at the given moment, not a general formula. During this stage, algebraic precision is essential because small errors propagate easily through rate calculations.
Step 8: Interpret the Result in Context
Interpretation is a critical stage in related rates problems because the computed value must make sense within the situation. Interpretations should include the quantity changing, the instant when it is changing, the direction of change (increasing or decreasing), and the units associated with the rate.
Organizational Strategies for Accuracy
To follow this procedure effectively, maintain orderly work throughout the problem. Students can enhance accuracy by using structured lists and clearly labeled steps.
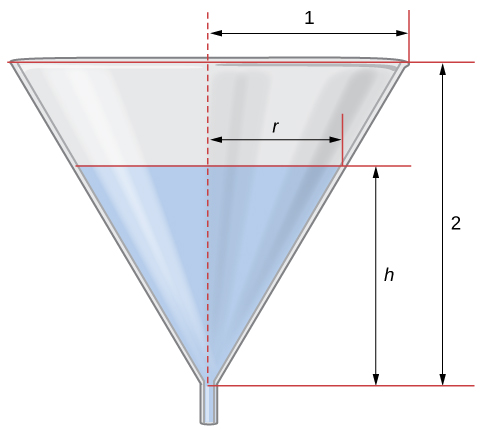
This figure shows a cone-shaped funnel of fixed height and top radius, partially filled with water whose height hhh and surface radius rrr change over time. The labeling highlights fixed dimensions and changing variables so that geometric relations such as can be applied systematically. The specific numerical values shown exceed syllabus requirements but illustrate the general structure of a multi-variable related rates setup. Source.
Useful organizational strategies include:
Writing all variable definitions before beginning any calculus.
Recording each rate with proper units to avoid mismatches after substitution.
Conserving symbolic expressions until differentiation is complete.
Labeling each stage of the process to maintain logical flow.
Why This Systematic Approach Matters
Related rates problems often involve multiple moving parts, and the relationships among variables can shift depending on context. A reliable method ensures that every derivative corresponds to the correct variable and that time remains the consistent independent variable. Without this structure, students may inadvertently mix quantities, omit essential dependencies, or misinterpret the resulting rate.
The step-by-step approach outlined here aligns directly with the AP Calculus AB syllabus expectation that students can “draw a diagram, write an equation relating variables, differentiate implicitly with respect to time, substitute known values, and solve for the desired rate.” By internalizing this structure, students prepare themselves to tackle related rates problems across a range of geometric, physical, and applied situations with accuracy and confidence.
FAQ
Time provides a consistent reference for comparing how multiple quantities change simultaneously. Even if a variable is not explicitly expressed as a function of time, it changes because the situation itself evolves over time.
Using time prevents mixing incompatible rates and ensures that each derivative represents a physically meaningful change. It also allows different types of quantities — lengths, areas, volumes, angles — to be connected within one coherent framework.
Choose the variable most closely tied to the physical change driving the scenario. For example, if water is being poured, the volume is the natural primary variable.
You can also look for:
• Quantities with known rates
• Variables with clearer geometric relationships
• Variables whose derivatives directly answer the question
The primary variable does not need to be solved for directly but often simplifies the differentiation process.
A good diagram clarifies which dimensions are fixed, which are changing, and how the quantities depend on each other. It should also visually separate constant lengths from variable ones.
Effective diagrams usually include:
• Arrows indicating direction of change
• Clear distinction between static boundaries and dynamic quantities
• Enough detail to form a correct equation, but never unnecessary clutter
Substituting early collapses the relationship into constants, eliminating the ability to apply differentiation correctly. Related rates require recognising how variables jointly change, which is only visible in symbolic form.
Preserving variables until after differentiation ensures:
• All dependencies between quantities remain intact
• The resulting derivative expresses an actual relationship between rates
• Fewer algebraic errors caused by prematurely removing variables
Interpret the sign, magnitude, and units of your result relative to the real situation. A negative rate should correspond to a quantity decreasing at that moment, while a positive one indicates growth.
You can also check reasonableness by asking:
• Does the direction match the described motion or change?
• Are the units consistent with the rate type (e.g., metres per second)?
• Is the magnitude plausible for the physical setting?
Practice Questions
Question 1 (1–3 marks)
A spherical balloon is being inflated, and its radius is increasing at a constant rate of 0.4 centimetres per second. Write an equation showing the relationship between the rate of change of the balloon’s volume and the rate of change of its radius, and hence state the expression for dV/dt in terms of r.
Question 1
• 1 mark for stating or using the correct volume formula for a sphere:
V = (4/3)πr³
• 1 mark for differentiating implicitly with respect to time:
dV/dt = 4πr² dr/dt
• 1 mark for substituting dr/dt = 0.4 to obtain the expression
dV/dt = 4πr²(0.4) or equivalent simplified form.
Total: 3 marks
Question 2 (4–6 marks)
A ladder 5 metres long rests against a vertical wall. The bottom of the ladder is being pulled away from the wall at a rate of 0.3 metres per second.
(a) Write an equation relating the height of the ladder on the wall, y, to the horizontal distance of the base of the ladder from the wall, x.
(b) Differentiate your equation with respect to time to relate dy/dt and dx/dt.
(c) Find dy/dt at the instant when x = 3 metres. State whether the top of the ladder is moving up or down the wall at this moment.
Question 2
(a) • 1 mark for correctly relating x and y using the Pythagorean theorem:
x² + y² = 25
(b) • 1 mark for differentiating implicitly with respect to time:
2x dx/dt + 2y dy/dt = 0
(c) • 1 mark for substituting x = 3 and dx/dt = 0.3 into the differentiated equation.
• 1 mark for correctly finding y using x² + y² = 25, giving y = 4.
• 1 mark for solving for dy/dt, obtaining a negative value and stating that the top of the ladder is moving down the wall.
Total: 6 marks

