Geometric related rates problems examine how areas, volumes, or related measurements change over time when one variable’s rate is known, emphasizing differentiation of formulas linking geometric quantities.

Understanding Geometric Related Rates

Geometric related rates problems involve quantities connected through geometric formulas whose values change with time. These problems require expressing how a geometric measurement varies as another dimension changes, typically using differentiation with respect to time.

When a problem involves a shape whose dimensions vary, each affected measurement becomes a time-dependent variable. Recognizing these variables is essential for correctly setting up a relationship that connects the changing quantities.

In geometric scenarios, the connection between quantities typically arises from formulas for area, volume, or perimeter, which must be differentiated implicitly to reveal how rapidly the associated measurements vary.

Using Geometric Formulas in Related Rates

Geometric relationships provide the foundational equation from which all subsequent differentiation emerges. Before differentiating, it is necessary to write an equation containing only the variables relevant to the changing quantities in the problem.

A sentence here clarifies that geometric rate relationships often require isolating variables and sometimes substituting known constraints before differentiating.

These foundational formulas allow one to connect the change of one dimension to the change of another through differentiation with respect to time.

Differentiating Geometric Relationships

Once the geometric equation is identified, the next step is differentiating both sides with respect to time, even if the equation itself does not explicitly involve time. Because dimensions such as radius, height, or side length vary with time, each variable must be treated as a function of time.

When differentiating a formula such as $A = \pi r^{2}$, the derivative incorporates the chain rule because $r$ changes over time, producing $\frac{dA}{dt} = 2\pi r\frac{dr}{dt}$. This expression explicitly links two rates: the rate at which the radius changes and the resulting rate at which the area changes.

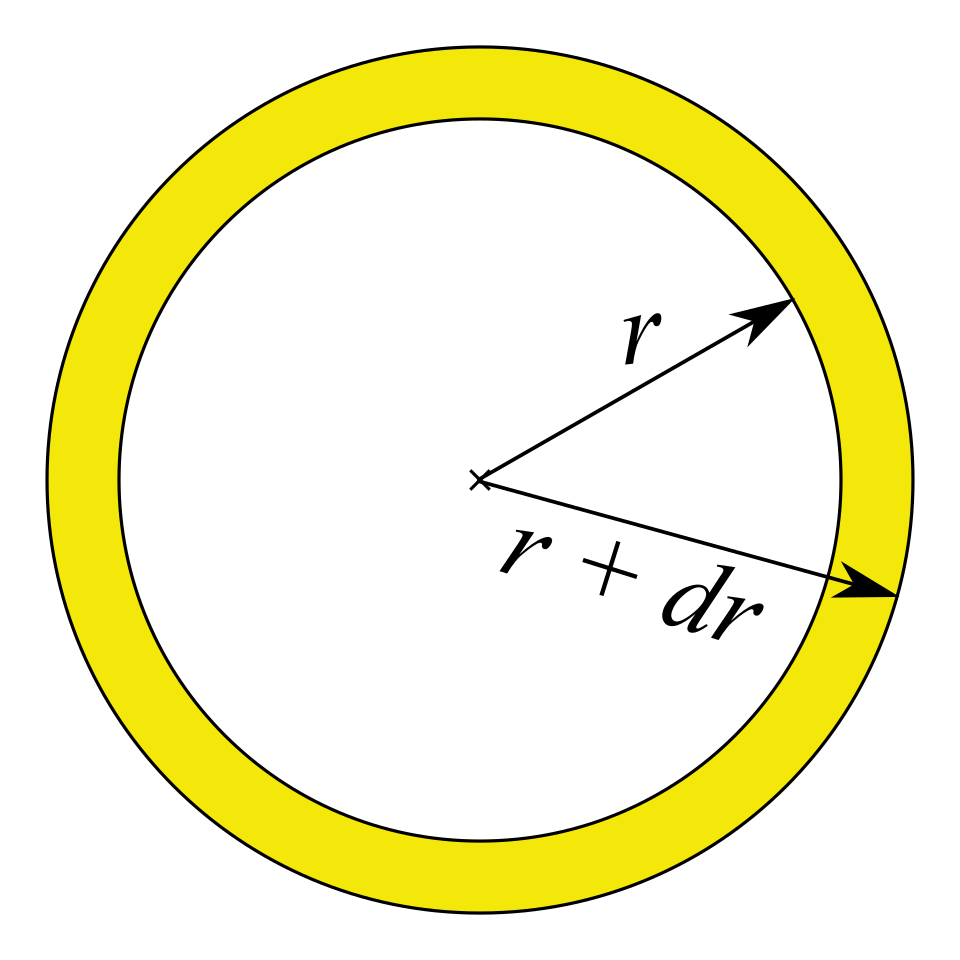
A circle with a thin yellow ring highlights the differential increase in area when the radius changes by a small amount. The shaded annulus corresponds to the relationship between circumference and area change. This diagram also hints at how integrating these differential areas gives the full formula $A = \pi R^{2}$. Source.

Similarly, differentiating volume formulas such as $V = \frac{4}{3}\pi r^{3}$ yields $\frac{dV}{dt} = 4\pi r^{2}\frac{dr}{dt}$. This step is central in geometric related rates problems because it produces the equation that directly relates known and unknown rates.

Interpreting Area-Based Rates

Area-related problems frequently involve shapes whose dimensions are expanding or contracting, and the rate of change of area depends not only on how fast a dimension changes but also on the current size of that dimension. In circles, a small increase in radius produces a much larger increase in area when the radius itself is large. Understanding this sensitivity to scale is essential for conceptual clarity.

For polygons or composite shapes, related rates might involve relationships between side lengths or angles. Even when the problem appears to involve multiple changing dimensions, the geometric constraints often reduce the number of variables.

Interpreting Volume-Based Rates

Volume-related problems often arise in contexts such as fluid flow, filling or emptying containers, or objects expanding uniformly. Differentiating a volume formula makes clear that the rate of volume change depends on the shape’s geometry at that instant.

When dealing with solids like spheres, cones, or cylinders, students must connect the changing dimension—whether a radius, height, or both—to how rapidly the entire volume changes.

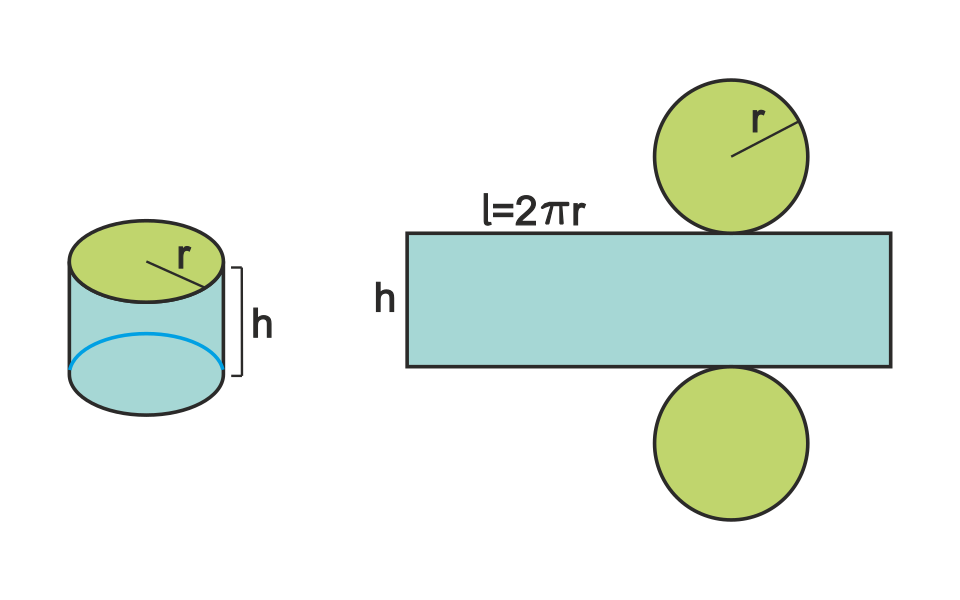
An unfolded cylindrical net displays how the radius and height define the structure of a cylinder. This helps illustrate why formulas such as $V = \pi r^{2}h$ depend directly on these measurements. The inclusion of the full net offers geometric insight into the relationships used in related rates problems. Source.

Because volume formulas typically involve higher powers, even moderate changes in a single dimension can produce large changes in volume.

Structure of a Geometric Related Rates Solution

Although the focus here is on conceptual understanding rather than step-by-step examples, geometric related rates problems consistently follow a clear structure. Students should be comfortable applying this structure:

• Identify geometric quantities that vary with time.

• Write the geometric formula connecting these quantities.

• Differentiate implicitly with respect to time, ensuring each variable is treated as time-dependent.

• Substitute known values at the instant of interest to find the desired rate.

• Express units clearly, reflecting area per unit time or volume per unit time as appropriate.

Units and Interpretation in Area and Volume Rates

Rates involving area typically use units such as square meters per second, while volume rates use cubic meters per second. Correct unit interpretation reinforces conceptual understanding of what the derivative represents in geometric contexts. Understanding these units ensures that students not only compute a value but also interpret its meaning in a way aligned with the AP Calculus AB syllabus.

A graduated measuring cylinder illustrates a real-world container whose liquid height and volume may change over time. This visual supports interpreting how cylinder-based volume formulas connect to observable measurements. The realistic detail goes slightly beyond the syllabus focus but reinforces the connection between geometry and applied rate problems. Source.