Understanding when a tangent line approximation gives an overestimate or underestimate helps students judge the reliability of linearization and interpret how concavity shapes a function’s local behavior.

Overestimates and Underestimates with Tangent Lines

Tangent line approximations rely on the idea that differentiable functions are locally linear, meaning the tangent line at a point can approximate nearby function values. Determining whether this approximation lies above or below the actual function is essential for correct interpretation. This topic focuses on how concavity, revealed through the sign of the second derivative, dictates whether the tangent line will overestimate or underestimate the true value of a function near a point of tangency.

When working with a differentiable function $f(x)$, its tangent line at $x=a$ provides a linear approximation, sometimes called a local linearization. Whether this line stays above or below the function depends entirely on how the function curves—its concavity—around $x=a$.

Understanding Concavity in This Context

Concavity describes how a function bends, and its sign indicates whether the graph opens upward or downward. The tangent line sits differently relative to this curvature, which is what leads to overestimates and underestimates.

A sentence here separates definition/equation blocks to meet formatting rules.

Concavity plays the authoritative role in determining approximation behavior:

• Concave up (f''>0) → function lies above its tangent line.

• Concave down (f''<0) → function lies below its tangent line.

These relationships are fundamental for identifying the type of estimation produced by the tangent line near the point of tangency.

How Concavity Determines Overestimates and Underestimates

The position of the tangent line relative to the function determines whether the approximation over- or underestimates the actual value. This comparison depends entirely on the sign of $f''(a)$ at the point of tangency.

When the Function Is Concave Up

If f''(a) > 0, the graph bends upward. The tangent line touches the graph at $x=a$ but otherwise stays below the curve in a neighborhood around that point. Therefore, any tangent line approximation for nearby $x$-values yields an underestimate of the true function value.

Key characteristics:

• The slope of the tangent line matches $f'(a)$, but the function increases at a faster rate due to upward bending.

• The curvature lifts the graph above the linearization.

• The difference between the function and tangent line grows as one moves farther from $a$.

When the Function Is Concave Down

If f''(a) < 0, the graph bends downward. In this case, the tangent line lies above the actual function for $x$-values close to $a$. This produces an overestimate of the true value.

Key characteristics:

• The tangent line keeps rising (or falling) at a constant rate, but the function’s rate of change decreases due to downward bending.

• The curvature pushes the graph below the tangent line.

• Overestimates become larger the farther one moves from the point of tangency.

For a concave down function near $x=a$, the graph bends like an upside-down bowl, and the tangent line lies above the curve close to the point of tangency.

Graph of $y=\cos(x)$ with multiple tangent lines illustrating local linear approximations. Near $x=0$, the function is concave down, so the tangent lines lie above the curve, producing overestimates. Multiple tangent points are shown to emphasize that this behavior occurs repeatedly along the curve. Source.

Bullet List Summary for Fast Identification

• Concave up (f''>0)

  • Tangent line is below the function.

  • Tangent line approximation is an underestimate.

• Concave down (f''<0)

  • Tangent line is above the function.

  • Tangent line approximation is an overestimate.

Interpreting the Behavior Graphically

Graphical interpretation reinforces the conceptual understanding of concavity and estimation type. Visualizing the function’s curvature clarifies how the tangent line compares to the actual function values:

• For a concave-up curve, the upward bend lifts the function away from the straight-line approximation.

• For a concave-down curve, the downward bend pulls the function beneath the tangent line.

These conceptual pictures help students connect abstract derivative behavior to intuitive graph shapes.

Using Concavity to Support Accurate Judgments

Concavity analysis ensures correct qualitative decision-making in applied problems. When interpreting real-world scenarios—such as approximating quantities related to growth, decay, or rates—students must consider whether the approximation logically fits the underlying curvature of the function. Failing to evaluate concavity can lead to incorrect assumptions about the direction and magnitude of error in tangent line approximations.

At a point where the function changes from concave down to concave up, the tangent line crosses the graph at an inflection point, and tangent-line estimates switch from overestimates to underestimates (or vice versa).

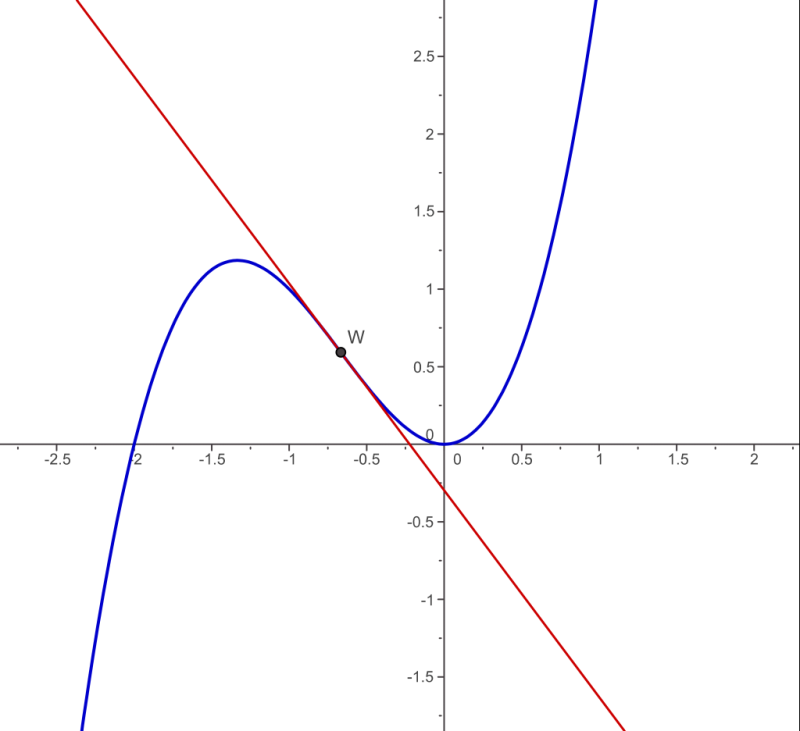
Graph of $y = x^3 + 2x^2$ with a tangent line at its inflection point. To the left, the curve is concave down and the tangent line lies above the graph, giving overestimates; to the right, concave up behavior makes the tangent line fall below the graph, giving underestimates. The explicit function extends slightly beyond syllabus requirements but clearly illustrates the concavity change and its effect on linearization. Source.

Practical Strategy for Students

When determining the nature of a tangent line approximation, rely on the second derivative:

• Identify $f''(a)$ and its sign.

• Use concavity to determine the relative position of the tangent line.

• Conclude whether the tangent line approximation produces an overestimate or underestimate for nearby values of $x$.

This structured reasoning ensures clarity, precision, and adherence to AP expectations in analyzing tangent line behavior.