The First Derivative Test provides a systematic way to determine whether a critical point marks a local maximum, a local minimum, or neither by examining how the sign of the derivative changes around that point.

Understanding the Role of the First Derivative Test

The First Derivative Test connects the behavior of the derivative to the overall shape of a function. Because the derivative describes the instantaneous rate of change, a shift in its sign reveals whether a function transitions from increasing to decreasing or vice versa. This method allows us to classify the nature of a critical point without relying on second derivative information.

Critical Points and Their Importance

A critical point is a point on the graph where the first derivative equals zero or does not exist, provided the original function is defined at that point. These points are essential because local extrema, when they exist, must occur at critical points. The First Derivative Test gives a reliable framework for analyzing these situations.

Before applying the test, it is necessary to understand how the derivative’s sign indicates whether a function is increasing or decreasing. These ideas form the basis for interpreting the sign change that determines the classification of the critical point.

The Statement of the First Derivative Test

The First Derivative Test evaluates what happens to the sign of $f'(x)$ as we move through a critical point. The AP syllabus emphasizes the underlying principle:

How the Test Works

To apply the test, examine the sign of $f'(x)$ immediately to the left and right of a critical point $c$. Interpret the meaning of those signs using the following logical structure:

• If $f'(x)$ changes from positive to negative as we pass through $c$, the function transitions from increasing to decreasing.

  • This pattern indicates a local maximum at $c$.

• If $f'(x)$ changes from negative to positive, the function transitions from decreasing to increasing.

  • This pattern indicates a local minimum at $c$.

• If $f'(x)$ does not change sign, the behavior of the function does not switch from increasing to decreasing or vice versa.

  • In this case, the point is neither a local maximum nor a local minimum, but it remains a critical point.

These sign changes provide information that is purely local, meaning the classification is based only on the function’s immediate neighborhood around the point, without requiring global information about the entire interval.

The First Derivative Test uses sign changes in f′(x) around a critical point to determine whether that point is a local maximum, a local minimum, or neither.

A graph illustrating local and global maxima and minima, showing how peaks and valleys correspond to the types of extrema identified using the First Derivative Test. The image also distinguishes global from local extrema, which slightly exceeds this subsubtopic but remains helpful for interpreting the test’s conclusions. Source.

Why the Test Is Reliable

The strength of the First Derivative Test lies in its use of the derivative’s sign, which directly reflects the increasing or decreasing behavior of the function. A change in sign is equivalent to a change in direction of motion, making it possible to determine the exact nature of the turning point.

Because the derivative represents the slope of the tangent line, sign changes in f′(x) capture how the graph of f shifts from rising to falling, or from falling to rising.

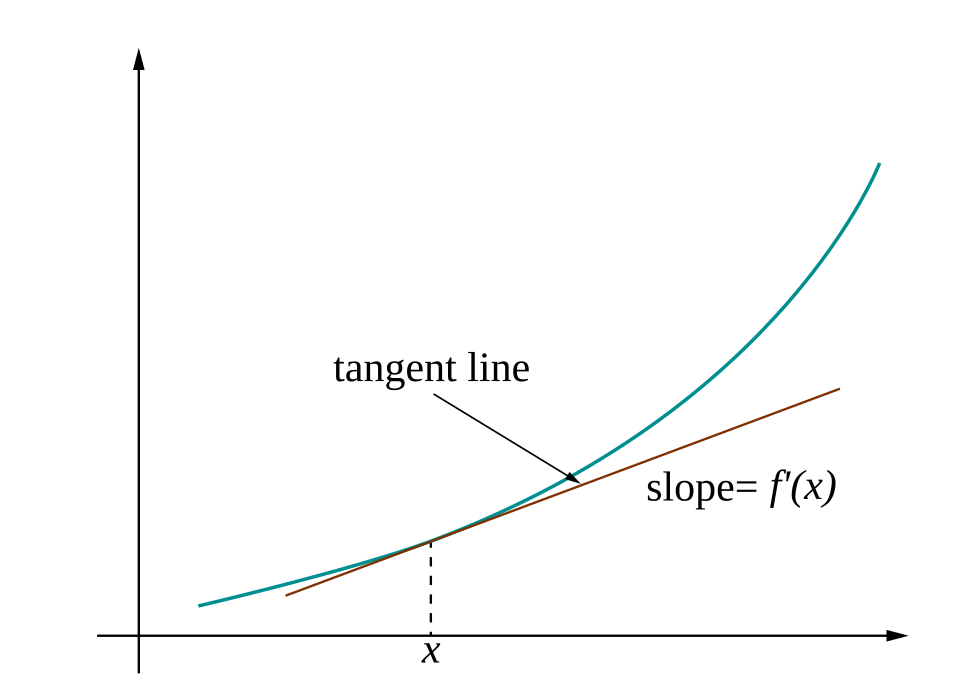
A curve with its tangent line is shown, representing how the sign of $f'(x)$ corresponds to the slope of the tangent. This visual reinforces the idea that interpreting slope is essential to understanding sign changes in the First Derivative Test. Source.

Applying the Test in a Structured Way

The classification procedure benefits from a consistent, repeatable structure. AP Calculus AB students should internalize the following process:

Step-by-Step Approach

• Identify all critical points of the function by finding where $f'(x)=0$ or where $f'(x)$ is undefined.

• Create intervals around each critical point to determine the sign of the derivative on each side.

• Evaluate the sign of $f'(x)$ within each interval rather than at the critical point itself.

• Compare the signs to determine whether a sign change occurs as you move through the critical point.

• Classify the point as a local maximum, local minimum, or neither using the First Derivative Test.

This structure ensures clarity and supports accuracy when analyzing the behavior near critical points.

Emphasizing Key Terminology

Students must be familiar with the specific vocabulary used within the test, including increasing, decreasing, sign change, and local extremum. Because AP Calculus relies on precise written justifications, correctly naming these ideas is essential for communicating reasoning in free-response contexts.

A full understanding of this terminology allows students to make accurate, well-structured statements using the First Derivative Test. This is especially important when explaining why a function attains a specific type of extremum at a particular point.

Interpreting Results Verbally

Clear interpretation is a central part of AP Calculus AB communication. Students should express First Derivative Test findings using precise language:

• Refer explicitly to the sign of the derivative.

• State clearly whether the derivative changes from positive to negative or negative to positive.

• Use formal phrases such as “the function is increasing on…” or “the derivative changes sign at…” to justify conclusions.

Strong verbal reasoning complements symbolic work and strengthens conceptual mastery, allowing students to connect derivative behavior with overall function shape.