This section explains how the First Derivative Test identifies a local minimum by examining how the sign of the derivative changes on either side of a critical point within an interval.

Identifying Local Minima Using the First Derivative Test

A local minimum occurs when a function’s value at a point is lower than the values at nearby points.

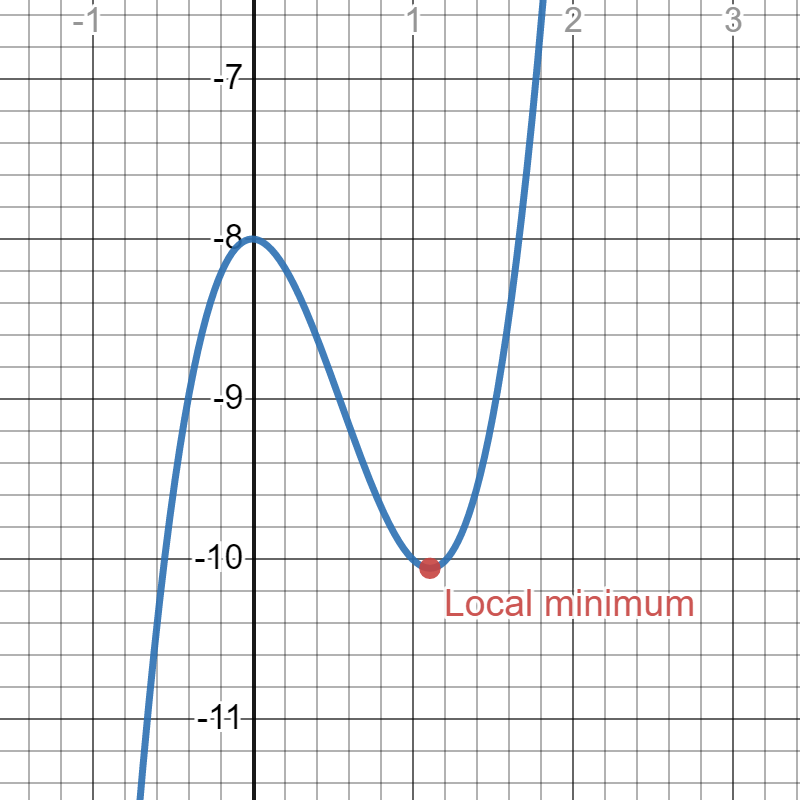
This graph shows a function with a clearly visible local minimum where the curve dips before rising again. The shape demonstrates how the function value at the minimum is less than the values nearby. The image does not explicitly show derivative values, so the connection to $f'(x)$ must be inferred from the slope of the curve. Source.

In the context of the First Derivative Test, the AP specification emphasizes that a function has a local minimum at a critical point when its derivative changes sign from negative to positive at that point.

When applying this test, recall that a critical point is any value of $x$ where the derivative is zero or undefined, as long as the original function is defined at that value. Critical points serve as candidates for local extrema, and the First Derivative Test allows us to classify them by analyzing the behavior of the derivative around the point.

Understanding the Role of the Derivative’s Sign

The derivative represents the instantaneous rate of change of a function. Examining its sign on an interval allows us to determine whether the graph is rising or falling.

After introducing the idea of increasing behavior, it is equally important to consider decreasing behavior to understand transitions.

Between these two behaviors lies the essential shift that allows a local minimum to occur. When the derivative changes from negative to positive, the function switches from decreasing to increasing, creating a point where the function’s value is locally the smallest.

How the Sign Change Creates a Local Minimum

To classify a local minimum using the First Derivative Test, focus on the structure of change in the derivative’s sign across the critical point. This approach is algebraic in nature but reveals a geometric idea: the function curves downward into a trough and then curves upward afterward.

Sign Change Pattern for a Local Minimum

A critical point becomes a local minimum if the derivative behaves as follows:

• The derivative is negative just to the left of the critical point.

• The derivative is zero or undefined at the critical point.

• The derivative is positive just to the right of the critical point.

This pattern indicates a shift from decreasing to increasing behavior.

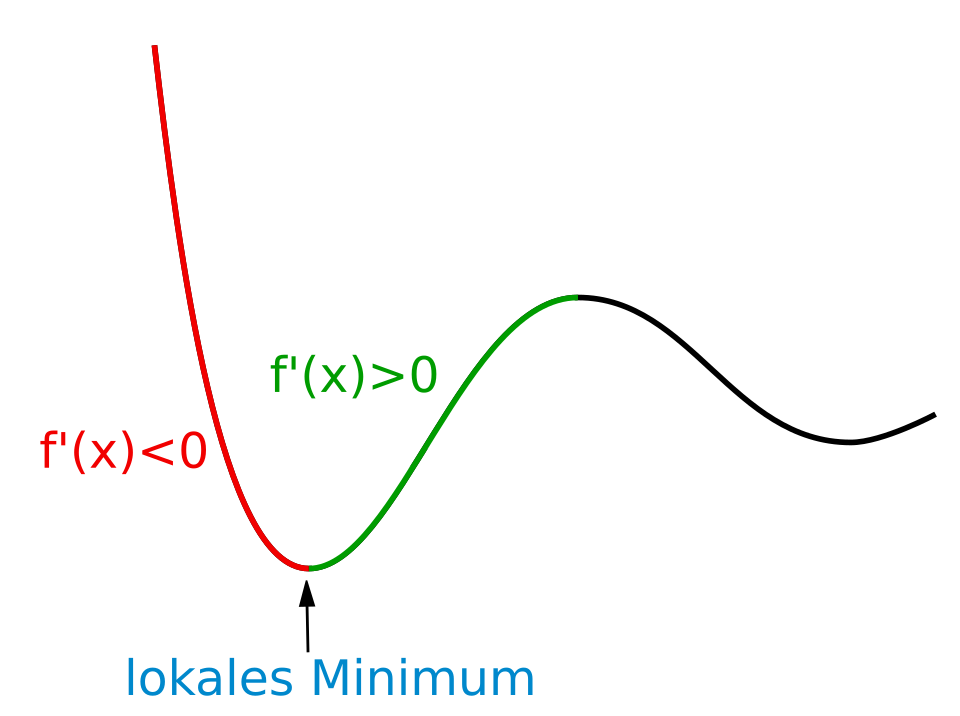
This schematic illustrates how a function decreases before the minimum and increases afterward, highlighting the sign change from negative to positive in $f'(x)$. The diagram uses simple curves and arrows to reinforce the structural behavior of a local minimum. Some labels appear in German and reference maxima, adding minor detail beyond this subsubtopic. Source.

Why This Pattern Creates a Minimum

A negative derivative means the function is sloping downward. As the function approaches the critical point, it continues decreasing. At the critical point, the slope levels out momentarily, resulting in a horizontal tangent if the derivative is zero. After that, a positive derivative indicates that the function begins to increase. This turning point forms a valley, which defines a local minimum.

Applying the First Derivative Test in Practice

To systematically determine whether a given critical point corresponds to a local minimum, use the following structured procedure.

Steps for Classifying a Local Minimum

• Identify the critical point: Solve $f'(x) = 0$ or determine where $f'(x)$ is undefined, provided the original function is defined at that $x$-value.

• Construct a sign chart: Select test points on intervals to the left and right of the critical point, and determine whether the derivative is positive or negative at those points.

• Evaluate the sign change:

  • If $f'(x)$ goes from negative to positive, classify the critical point as a local minimum.

  • If this pattern does not occur, the point is not a local minimum.

• Describe behavior in words: Clearly state the sign of the derivative on each side of the critical point to justify the classification.

Importance of Proper Justification

Because AP Calculus AB emphasizes conceptual understanding, students must provide justification using the derivative’s sign rather than simply reporting the result. A complete justification addresses three components:

• The derivative’s sign on the interval immediately to the left of the critical point.

• The derivative’s sign on the interval immediately to the right of the critical point.

• The conclusion that the derivative’s change from negative to positive implies a local minimum.

The justification highlights the function’s transition from decreasing to increasing, matching the required reasoning in the AP syllabus.

Geometric Interpretation of the Local Minimum

Understanding the geometric meaning strengthens intuition. When the derivative is negative, the tangent lines tilt downward. At the critical point, the tangent becomes horizontal. When the derivative becomes positive, tangent lines tilt upward. The function’s graph therefore descends, flattens, and then rises, producing a recognizable valley shape. This visualization aligns with the analytical condition provided by the First Derivative Test and reinforces the connection between algebraic derivative behavior and geometric curve shape.

Distinguishing Local Minima from Other Critical Points

Not all critical points yield local minima, so the sign change criterion is crucial. If the derivative does not change sign across a critical point, then the point is not a local extremum. This distinction prevents misclassification and encourages careful evaluation.

By focusing on the derivative's sign pattern and applying the First Derivative Test consistently, students can reliably classify local minima as required by AP Calculus AB.

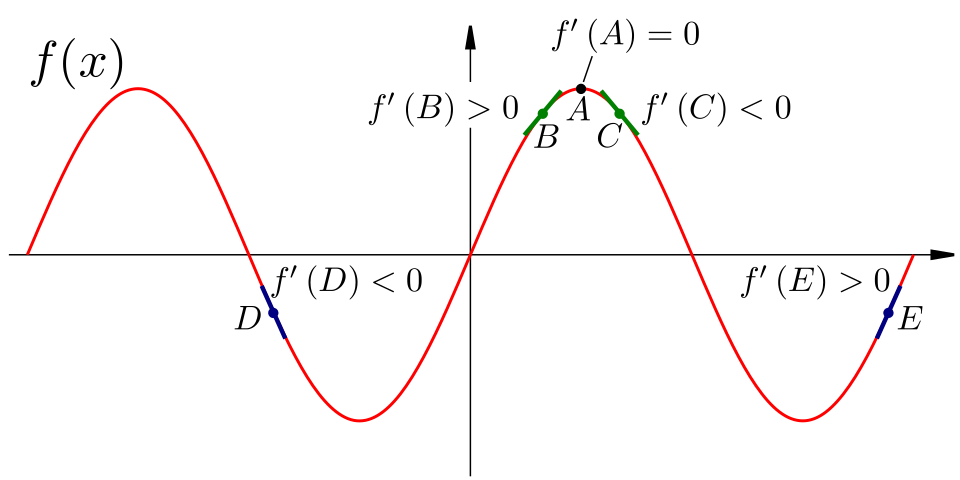
This diagram demonstrates how gradients at nearby points help determine whether a point is a maximum or minimum. Green arrows sample slopes correctly on both sides of a suspected extremum, while blue arrows illustrate incorrect testing positions. The figure includes both maxima and minima and uses vector-like gradients, extending slightly beyond the AP syllabus but reinforcing how $f'(x)$ must be checked on either side of the critical point. Source.