AP Syllabus focus:
‘If f′(x) changes from positive to negative at a critical point, then the function changes from increasing to decreasing and has a local maximum at that x-value.’
Understanding how to identify local maxima is essential for analyzing functions in calculus. The First Derivative Test offers a reliable, conceptual method grounded in derivative sign changes.
Classifying Local Maxima with the First Derivative Test
The First Derivative Test is a fundamental analytical tool in AP Calculus AB, allowing students to determine whether a critical point corresponds to a local maximum, local minimum, or neither. This subsubtopic focuses specifically on how to recognize when a function has a local maximum by examining changes in the sign of its first derivative, . It relies on understanding derivative behavior on intervals around the critical point and how that behavior reflects the underlying shape of the function.
Before applying the First Derivative Test, students must recall the role of the derivative in describing function behavior and the definition of a critical point, which lays the foundation for testing whether the point represents a maximum.
Critical Point: A point in the domain of a function where or where does not exist.
A local maximum is tied directly to how the function behaves immediately before and after the critical point, making the sign change in the derivative the essential feature.
The Role of the Derivative in Identifying a Local Maximum
A first derivative that is positive indicates that the function is increasing, while a derivative that is negative indicates that the function is decreasing. A local maximum occurs precisely when the direction of change shifts from increasing to decreasing at a specific x-value. This behavior is translated directly into a sign change in .
The AP specification highlights this criterion: If f′(x) changes from positive to negative at a critical point, then the function changes from increasing to decreasing and has a local maximum at that x-value.
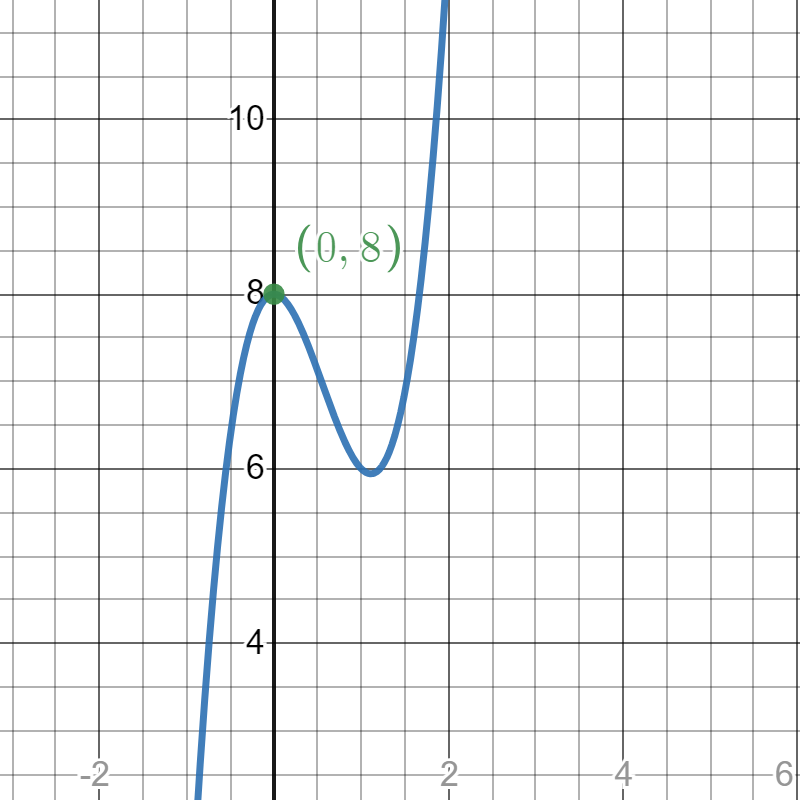
A smooth function rises to an interior peak and then falls, illustrating a local maximum. The function increases to the left of the peak and decreases to the right, reflecting the First Derivative Test condition before the point and after. The slope behavior is inferred from the graph’s shape rather than shown explicitly. Source.
Why a Sign Change Indicates a Maximum
The First Derivative Test relies on the intuitive geometric observation that a local maximum sits at a “peak” on the graph. If the function increases on the left of the point, it approaches the peak from below; if it then decreases on the right, it descends from the peak, ensuring the point is locally the highest.
This interpretation connects the algebraic derivative to the geometric shape of the graph. Because increasing behavior corresponds to slopes of tangent lines that are positive and decreasing behavior corresponds to negative slopes, the shift in sign of captures the full local behavior necessary to classify the point.
Process for Classifying a Local Maximum
When applying the First Derivative Test to classify local maxima, follow a structured analysis:
Identify all critical points by solving or locating where is undefined.
Verify that each critical point lies within the domain of the original function.
Create intervals around the critical point and determine the sign of on each side.
Observe the direction of change:
If on the interval to the left of the critical point and
on the interval to the right,
then the function has a local maximum at that x-value.
This set of checks ensures that the classification is based entirely on derivative behavior and remains fully consistent with the AP definition of a local maximum using the First Derivative Test.
Interpreting Derivative Sign Changes in Practice
When performing a sign analysis, the focus is not on the magnitude of but purely on whether it is positive or negative. Even a very small positive derivative indicates the function is rising there; a small negative derivative indicates it is falling. The test does not require computing actual function values, only determining the direction of change.
Because local maxima occur where behavior switches from increasing to decreasing, the sign chart becomes one of the most useful organizational tools. A simple visual inspection of signs surrounding the critical point is often the clearest method for classification.
Relationship Between the First Derivative Test and Function Shape
Once the derivative analysis is complete, students should be able to describe verbally how the function behaves near the local maximum. The function rises as it approaches the critical point, reaches a highest nearby value, and then falls as it moves away from the point. This aligns with both the conceptual and the geometric meaning of the derivative and reinforces the interpretive skills expected in AP Calculus AB.
Using the Test in Verbal Justifications
Because AP free-response questions often require written explanations, it is important to refer explicitly to the sign change in the derivative. A proper justification typically includes:
The identification of the critical point,
A statement describing the sign of on either side of that point, and
A concluding sentence stating that the point is a local maximum because changes from positive to negative.
This graph displays a function with a clear interior peak representing a local maximum. Nearby points lie below the peak, illustrating that the value is locally greatest. The visual emphasis supports identifying the point as a local maximum using the First Derivative Test’s sign-change criterion. Source.
Emphasizing the derivative’s sign ensures that explanations remain aligned with the First Derivative Test rather than appealing to intuition or relying on the appearance of the graph alone.
Importance of Domain Awareness
The derivative test applies only when the critical point lies within the domain of the function. If changes sign around a value not included in the domain, the point is not considered for extrema. Recognizing domain restrictions prevents misclassification and ensures proper use of the test.
Linking the First Derivative Test to Broader Function Analysis
Classifying local maxima is a key step in analyzing the overall behavior of a function. Once maxima are identified, they contribute to understanding the function’s graph, aiding in interpreting increasing and decreasing intervals and providing a foundation for deeper applications such as optimization.

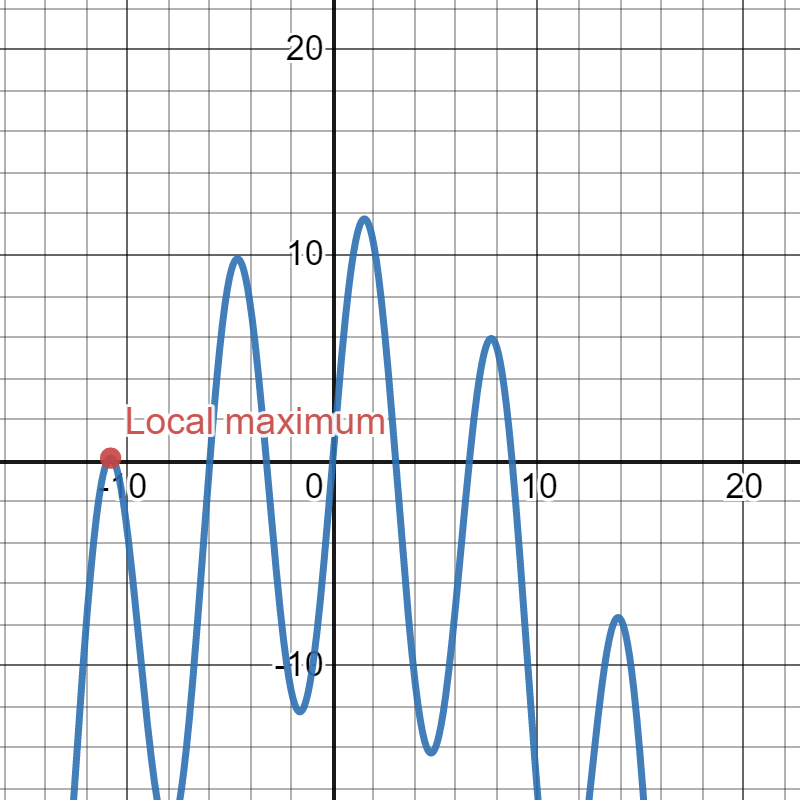
This diagram shows a function with multiple extrema, including local maxima identified by their peak positions. Points classified as local maxima occur where the curve rises and then falls, mirroring the First Derivative Test requirement that changes from positive to negative. The image also includes global extrema and local minima, which provide additional context beyond the immediate subsubtopic. Source.
FAQ
You only need to determine whether the derivative is positive or negative on each side of the critical point; the exact value is irrelevant.
A very small positive value still indicates the function is increasing, while a very small negative value indicates it is decreasing.
Choose test points that are clearly within the intervals but do not need to be especially close to the critical point.
Yes, a function may have several local maxima close to one another if it oscillates or changes direction repeatedly.
The First Derivative Test treats each critical point independently.
• Each time the derivative switches from positive to negative, that point is identified as a local maximum.
• The spacing between maxima does not affect the classification, only the sign change behaviour at each point.
In such cases, the First Derivative Test identifies the point as not being a local extremum.
This typically occurs at flat spots or points of inflection where the slope levels off briefly.
The function may continue increasing or decreasing without forming a peak.
The test still applies as long as the derivative exists on the open intervals around the critical point, even if it fails to exist at the point itself.
A sharp peak or cusp may still exhibit a clear sign change in the derivative on either side, revealing a local maximum.
The lack of differentiability at the point does not prevent classification.
If the critical point lies at an endpoint, the First Derivative Test cannot be applied because the derivative’s sign cannot be checked on both sides.
For interior points near boundaries, the test still works normally:
• Check the sign of the derivative on the side that exists within the domain.
• Only classify points where two-sided sign changes are possible; otherwise, classification must rely on other methods.
Practice Questions
(1–3 marks)
A function f has derivative f'(x). At x = 2, the derivative changes sign from positive to negative.
Explain what this implies about the behaviour of f at x = 2 using the First Derivative Test.
Question 1 (3 marks maximum)
• 1 mark: States that f has a critical point at x = 2.
• 1 mark: States that f'(x) changes from positive to negative at x = 2.
• 1 mark: Concludes that f has a local maximum at x = 2 by the First Derivative Test.
(4–6 marks)
The derivative of a function g is given for all x in the interval shown in the table:
x: 0 1 2 3 4
g'(x): -3 -1 0 2 -4
(a) Identify the x-value(s) where g has a critical point.
(b) Using the First Derivative Test, determine whether g has a local maximum, a local minimum, or neither at each critical point. Justify your answers using sign changes of g'(x).
(c) State the overall behaviour of g (increasing or decreasing) on each sub-interval determined by the critical points.
Question 2 (6 marks maximum)
(a) (1 mark)
• 1 mark: Correctly identifies x = 2 as the only critical point (where g' = 0).
(b) (3 marks)
• 1 mark: Notes that g'(x) is negative before x = 2 (e.g., at x = 1).
• 1 mark: Notes that g'(x) is positive after x = 2 until x = 3; then negative after x = 3, but for classification only the immediate change across 2 matters.
• 1 mark: Concludes that g has a local minimum at x = 2 because the derivative changes from negative to positive.
(c) (2 marks)
• 1 mark: Identifies intervals correctly: decreasing on (0,2), increasing on (2,3), and decreasing on (3,4).
• 1 mark: Provides a correct explanation relating each behaviour to the sign of g'(x).

