AP Syllabus focus:
‘If f′(x) does not change sign at a critical point, the First Derivative Test shows there is no local extremum there, even though the point is still critical.’
In the First Derivative Test, certain critical points resist classification because the derivative does not switch sign around them. Understanding why the test becomes inconclusive clarifies how functions behave near these subtle points.
When the First Derivative Test Fails to Classify a Critical Point
The First Derivative Test determines whether a function has a local maximum, local minimum, or neither at a critical point—a point where the derivative is zero or undefined. The test relies on detecting a change in sign of on either side of that point. When no sign change occurs, the test cannot identify a local extremum, leading to an inconclusive result.
The Role of Critical Points
A critical point is a point where the derivative behaves in a special way, often indicating interesting or important features of the graph. When or does not exist and lies within the domain of the function, the point is classified as critical. Critical points are locations where potential maxima, minima, or changes in behavior might occur.
Critical Point: A point in the domain where or does not exist.
Critical points, however, do not guarantee the presence of an extremum. They are merely candidates, and their classification depends entirely on how the derivative behaves around them.
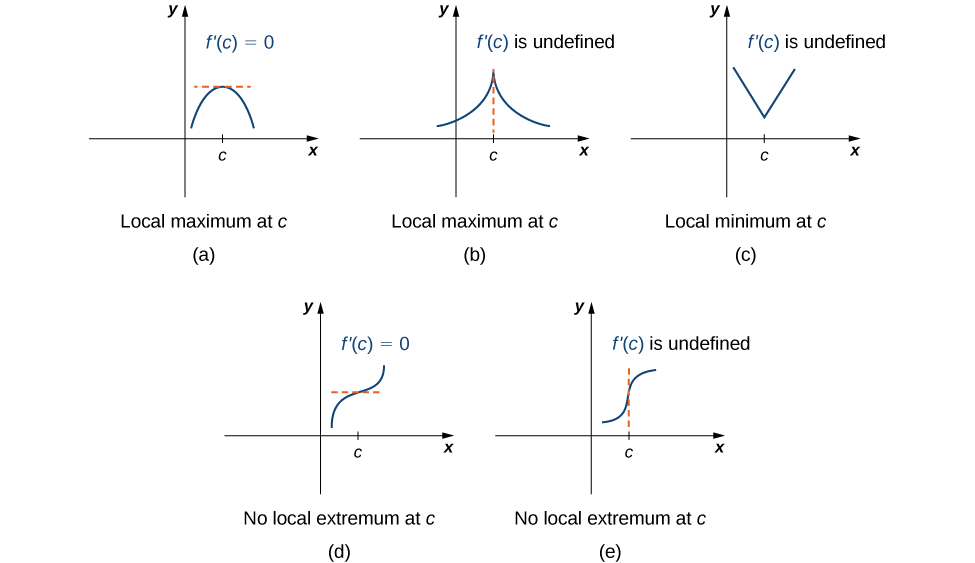
Composite figure with graphs showing cases where critical points may or may not correspond to extrema. Panels (d) and (e) illustrate situations where or undefined but the function has no local extremum, demonstrating why the First Derivative Test can be inconclusive. Extra detail: the diagram also includes true maxima and minima, which extends slightly beyond the specific syllabus focus. Source.
Why Sign Changes Matter
The First Derivative Test tests for sign changes in the derivative because these changes reflect transitions between increasing and decreasing behavior. A change from positive to negative indicates a turning point downward (a local maximum), while a change from negative to positive indicates a turning point upward (a local minimum). The absence of a sign change implies the function does not switch directions.
Some critical points represent points of inflection, plateaus, or flat regions where the function continues increasing or decreasing straight through the critical point without turning.
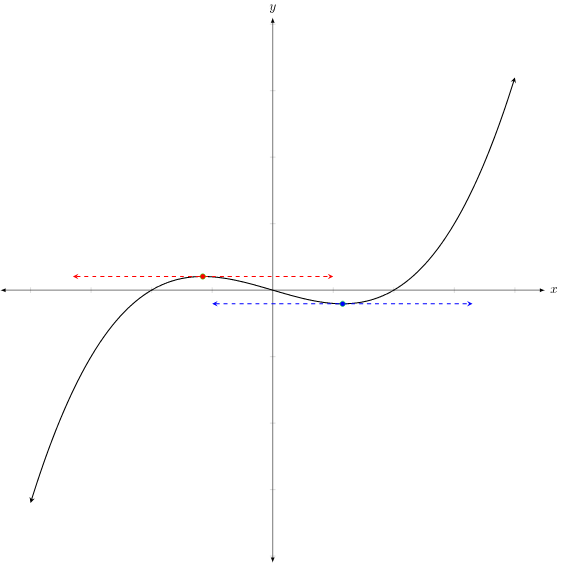
Graph of a function with a horizontal tangent at a critical point but no local extremum. The curve flattens at and continues increasing, showing that does not change sign and the First Derivative Test is inconclusive. Extra detail: the curve resembles a cubic function, providing one common model of this behavior. Source.
Understanding the Inconclusive Case
When the derivative remains positive on both sides of a critical point or remains negative on both sides, the First Derivative Test reports that the point is not a local extremum. Although the derivative may temporarily reach zero or fail to exist, the graph does not exhibit the turning behavior needed for maxima or minima.
Conditions Leading to an Inconclusive Test
Below are common situations in which the First Derivative Test does not provide classification:
Derivative zero but no direction change
is positive on both sides of
is negative on both sides of
Derivative undefined but no directional change
A sharp point or cusp exists, but the function keeps increasing or decreasing through the point
Flat spots or stationary inflection points
The derivative may equal zero, but concavity changes instead of direction
These situations align directly with the AP specification: even if a point is critical, the First Derivative Test may fail to classify it because no sign change occurs.
Typical Patterns in the Derivative’s Behavior
To analyze the inconclusive case clearly, it helps to consider the derivative’s behavior as one approaches the critical point:
Always positive
is increasing before and after the pointAlways negative
is decreasing before and after the pointMixed concavity
might flatten at the critical point but still not form a maximum or minimumConstant derivative near the point
Flat segments reflect no turning behavior
This reveals that critical points only signal potential extrema; the derivative’s sign pattern determines their actual nature.
How to Analyze a Critical Point When the Test Is Inconclusive
Although AP Calculus AB does not require alternative tests in depth, students must know what to do next when the First Derivative Test fails. The following steps expand your reasoning without crossing into another subtopic’s required techniques:
Steps for Further Investigation
Confirm the point is a true critical point by checking whether or does not exist.
Examine the sign of on both sides of the point using a sign chart, verifying that no change occurs.
Observe how the function behaves immediately around the point:
Does it keep rising?
Does it keep falling?
Does it flatten without turning?
Recognize that, per the AP definition, the function has no local extremum at this point.
These steps reinforce that the goal is not to classify using alternative tests, but simply to understand why the First Derivative Test declares the point inconclusive.
Interpreting Graphical Behavior
Graphs help illustrate inconclusive cases clearly. At such points, the graph may show:
A horizontal tangent where the curve continues increasing or decreasing
A sharp point where the curve moves through without switching direction
A stationary inflection point, where concavity changes but the direction of motion does not
In all cases, the essential idea holds: no change in monotonic behavior means no local extremum, aligning exactly with the AP syllabus requirement.
FAQ
An inconclusive First Derivative Test result occurs when a critical point exists but the derivative does not change sign around it. The test applies, but it cannot classify the point.
If there is no critical point, the test cannot be applied at all because there is no candidate point for an extremum.
In short, an inconclusive result means the test ran but produced no extremum; no critical point means the test cannot even begin.
Yes. A stationary point where the derivative does not change sign often corresponds to a point of inflection.
This occurs when the tangent is horizontal but the graph switches concavity instead of direction.
However, an inconclusive result does not guarantee an inflection point; it only rules out a local extremum.
Look at the behaviour of the function values immediately around the critical point.
You can:
• Compare values slightly to the left and right of the point.
• Check whether the function is strictly increasing or decreasing across it.
• Observe whether any flattening occurs only momentarily or consistently over an interval.
A turning point will show a directional change; a flat spot will not.
It can be difficult to interpret if the derivative values are very small, especially with numerical or graphical data.
However, as long as the derivative is strictly positive or strictly negative and maintains that sign, the test's conclusion remains valid.
The challenge lies not in the test itself but in accurately determining the sign of the derivative when values are near zero.
Yes. Some functions have extended flat regions, repeated stationary points, or oscillatory behaviour where the derivative touches zero repeatedly without changing sign.
In such cases:
• Each of those points is a critical point.
• None of them corresponds to a local extremum.
• The graph may oscillate gently or maintain monotonic behaviour despite multiple zeros of the derivative.
This is common in smooth functions that momentarily flatten at several nearby points without turning.
Practice Questions
(1–3 marks)
The function g is differentiable, and g has a critical point at x = 2 where g'(2) = 0. The derivative g' is positive for all x < 2 and positive for all x > 2.
State whether g has a local maximum, a local minimum, or neither at x = 2. Justify your answer using the First Derivative Test.
Question 1 (1–3 marks)
• 1 mark: Correct conclusion that g has neither a local maximum nor a local minimum at x = 2.
• 1 mark: Correct justification that g'(x) is positive on both sides of x = 2.
• 1 mark: Correct explanation that because there is no sign change in the derivative, the First Derivative Test shows no local extremum is present.
(4–6 marks)
A function f is differentiable on the real line. It is known that f'(1) = 0. The table below gives the sign of f'(x) on intervals around x = 1.
Interval Sign of f'(x)
x < 1 Negative
x = 1 Zero
x > 1 Negative
(a) Determine whether f has a local extremum at x = 1. Explain fully.
(b) Describe the behaviour of the graph of f near x = 1.
(c) State why the First Derivative Test is inconclusive for classifying a maximum or minimum at x = 1, even though f'(1) = 0.
Question 2 (4–6 marks)
• 1 mark: Correct conclusion in part (a) that f does not have a local maximum or minimum at x = 1.
• 1 mark: Recognition that f'(x) is negative on both sides of x = 1.
• 1 mark: Explanation in part (a) that the absence of a sign change means the First Derivative Test does not identify an extremum.
• 1 mark: In part (b), correct description that f is decreasing before and after x = 1, so the graph continues decreasing through x = 1.
• 1 mark: In part (c), correct explanation that although f'(1) = 0, the derivative does not change sign, so the test cannot classify the point as a maximum or minimum.
• 1 mark: Clear statement that x = 1 is still a critical point, even though it is not an extremum.

