AP Syllabus focus:
‘A graph is concave up on an open interval if its first derivative is increasing there, and concave down if its first derivative is decreasing on that interval.’
Concavity describes how a function bends and helps reveal deeper behavior than simple increases or decreases. Understanding how the first derivative changes clarifies a graph’s overall shape.
Concavity and the First Derivative
Concavity provides insight into how the rate of change of a function behaves on an interval. When studying a differentiable function, analyzing the first derivative shows whether the graph bends upward or downward. This perspective helps students connect geometric intuition with algebraic reasoning.
Understanding Concavity Through f′
Concavity is fundamentally about how the slope of the tangent line evolves. Because the slope at each point is determined by the first derivative, examining how that derivative behaves across an interval reveals how the graph is shaped.
Geometrically, a graph is concave up on an interval if the slopes of its tangent lines are increasing from left to right, and concave down if those slopes are decreasing.
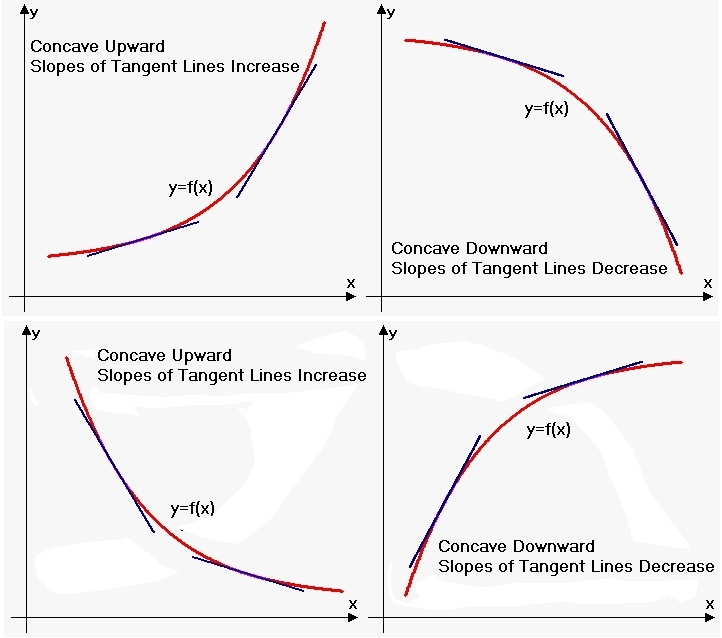
This figure compares concave up and concave down graphs using tangent lines. In the concave up panels, tangent slopes increase from left to right, while in the concave down panels they decrease. The image emphasizes that concavity is determined by how slopes change across an interval. Source.
Concave Up: The graph of a function bends upward on an interval when the slopes of its tangent lines increase across that interval.
A function is concave up when its first derivative is increasing, matching the syllabus statement. This increasing slope creates a shape that opens upward, reflecting continuously rising tangent-line slopes.
Concave Down: The graph of a function bends downward on an interval when the slopes of its tangent lines decrease across that interval.
Concave down behavior corresponds to a first derivative that is decreasing. The slope becomes smaller as x increases, causing the graph to bend downward.
These descriptions connect the graph’s curvature with changes in the first derivative without requiring second derivative formulas, maintaining focus on the syllabus requirement.
Visualizing Concavity With Changes in f′
Understanding how f′ behaves across intervals is central to describing concavity. Students should train themselves to observe how slope values change, not just whether they are positive or negative.
Interpreting Increasing and Decreasing Slopes
To determine concavity using only f′:
If f′ is increasing, the function is concave up on that interval.
If f′ is decreasing, the function is concave down on that interval.
This method aligns directly with the syllabus description and avoids confusion between derivative sign and derivative trend. A positive derivative simply means the function is increasing, but an increasing derivative means the graph is bending upward. The distinction between the value of f′ and how that value changes is a core conceptual insight in this topic.
Why Increasing or Decreasing f′ Matters
Because f′ measures slope, any trend in f′ reflects a trend in slope:
When slopes grow larger moving left to right, the curve must bend upward.
When slopes grow smaller, the curve must bend downward.
This reasoning provides geometric intuition. Students see that concavity is not about steepness alone but about how steepness evolves.
Using Graphs or Tables of f′ to Describe Concavity
Concavity can be analyzed using various representations of the first derivative, and each approach reinforces the same core idea.
From a Graph of f′
When given a graph of the first derivative:
An increasing graph of f′ indicates concave up behavior for the original function.
A decreasing graph of f′ indicates concave down behavior.
Students should focus on the trend of the graph rather than individual values. Even if f′ is negative, the function can still be concave up if the derivative is increasing, because the slopes become less negative over time.
From a Table of f′ Values
When provided a table:
Look for entries where f′ values rise as x increases, indicating concave up behavior.
Look for decreasing sequences of f′ values to conclude concave down behavior.
Tables emphasize numerical reasoning about slopes and strengthen conceptual understanding without reliance on algebraic expressions.
Key Points for Analytical Interpretation
Because concavity depends on changes in the first derivative, accurate interpretation requires clear reasoning about slope trends. Students should consistently connect these ideas to the syllabus phrasing about f′ increasing or decreasing.
At each point on the graph, the tangent line represents the instantaneous rate of change of the function, the value of the first derivative at that x-value.
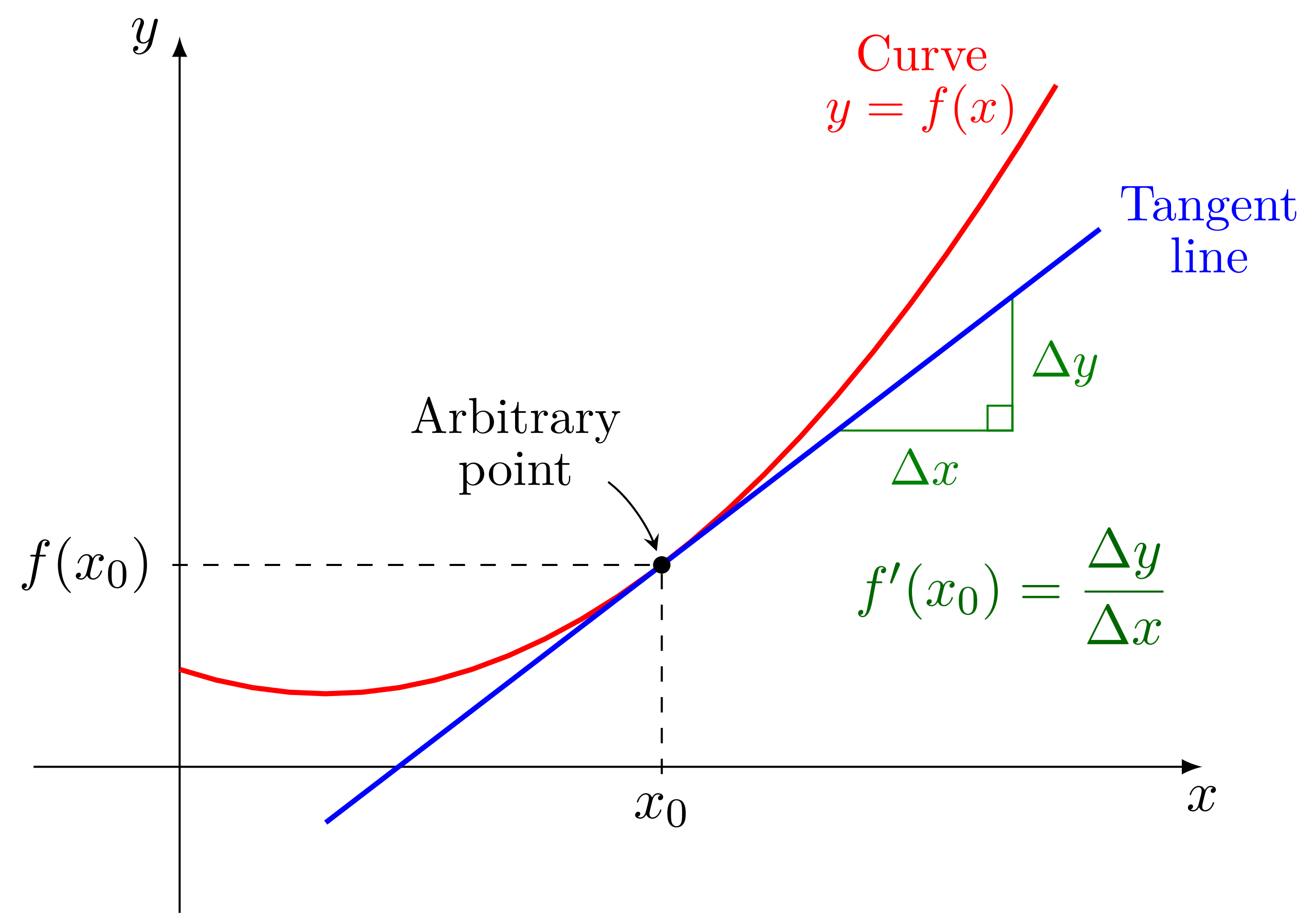
This graphic shows a smooth curve together with its tangent line at a single point of contact. The slope of the tangent line represents the instantaneous rate of change of the function at that point, corresponding to the value of the first derivative. Recognizing tangent lines as slopes at a point supports understanding how changing slopes determine concavity. Source.
Essential Interpretive Notes
Concave up does not mean the function is increasing; it means the slope is increasing.
Concave down does not mean the function is decreasing; it means the slope is decreasing.
Concavity statements apply only to intervals, not individual points.
The analysis assumes the function is differentiable over the interval being considered.
Practical Strategy for Students
To determine concavity efficiently:
Identify whether f′ is growing or shrinking as x increases.
Describe the resulting concavity using precise terminology.
Connect the behavior of f′ directly to how the graph bends.
Avoid confusing sign (positive/negative) with trend (increasing/decreasing).
This structured approach ensures alignment with the AP syllabus and supports clear, mathematically sound justifications when describing function behavior.
FAQ
An increasing first derivative means the slope values grow larger as x increases, regardless of whether those slopes are positive or negative. It describes a trend.
A positive first derivative simply means the slope is above zero, indicating the function is increasing, but this gives no information about how the slope is changing.
To determine concavity, focus on the trend of the slope values, not just their sign.
Concavity is determined by how the slope changes, not by whether the function rises or falls.
A decreasing function is concave up when its negative slopes become less negative across an interval. This means the function is still declining, but its rate of decrease is slowing.
This scenario is common when a function approaches a minimum or levels off after a steep drop.
Visual cues can help you infer the behaviour of the first derivative:
• When the graph bends upwards and slopes gradually steepen, f′ is increasing.
• When the graph bends downward and slopes flatten or tilt more sharply downwards, f′ is decreasing.
Even without exact values, observing how tangent lines would look gives insight into concavity.
Yes—concavity is often identifiable even on an approximate graph.
Look for whether the curve bends like a cup (concave up) or an arch (concave down).
Focus on how the steepness changes: do slopes become steeper or flatter as x increases?
Although precise values are unnecessary, you must be careful with sketches that are not smooth, as concavity analysis assumes differentiability.
Concavity reveals how a quantity's rate of change evolves over time.
For motion graphs, concave up behaviour means speed is increasing, while concave down behaviour signals slowing.
For growth curves, concave up indicates accelerating growth, whereas concave down shows diminishing returns.
By examining whether the slope trend increases or decreases, you gain insight into underlying processes without computing second derivatives.
Practice Questions
Question 1 (1–3 marks)
A function f is differentiable on an open interval. The following table gives selected values of its first derivative f′.
x: 1 2 3 4
f′(x): -5 -3 -1 0
(a) Determine whether the graph of f is concave up or concave down on the interval 1 < x < 4.
(b) Give a brief reason for your answer.
Mark Scheme for Question 1
• Correct statement that the graph is concave up on 1 < x < 4. (1 mark)
• Reason: f′ is increasing (the slope values become less negative), indicating concave up behaviour. (1–2 marks)
Total: 2–3 marks depending on clarity.
Question 2 (4–6 marks)
A differentiable function g has a first derivative g′ whose behaviour is described as follows:
• g′(x) decreases on the interval -2 < x < 0
• g′(x) increases on the interval 0 < x < 3
(a) State the concavity of the graph of g on each interval.
(b) At x = 0, g′ is continuous and equals -4. Explain why x = 0 may be a point where the concavity of g changes, and describe what this means for the shape of the graph.
(c) Without calculating any second derivative, explain how the behaviour of g′ alone allows you to justify your conclusions.
Mark Scheme for Question 2
(a)
• Correct concavity on -2 < x < 0: concave down (g′ decreasing). (1 mark)
• Correct concavity on 0 < x < 3: concave up (g′ increasing). (1 mark)
(b)
• Recognition that concavity changes at x = 0 because g′ switches from decreasing to increasing. (1 mark)
• Description that this indicates a possible point of inflection. (1 mark)
(c)
• Explanation that concavity is determined by whether g′ is increasing or decreasing, without needing g″; increasing g′ implies concave up and decreasing g′ implies concave down. (1–2 marks)
Total: 5–6 marks depending on detail and completeness.

