This shows why the Second Derivative Test can fail to classify a point and how to proceed when curvature information is insufficient for determining behavior.

When the Second Derivative Test Fails

Understanding when the Second Derivative Test becomes inconclusive is essential because not all critical points behave predictably under curvature analysis. Although the test often provides a quick way to classify extrema, some functions have points where second‐derivative information is too weak or unavailable to reveal local behavior. In such cases, AP Calculus AB students must rely on alternative derivative-based strategies.

A critical point is an $x$-value where $f′(x)=0$ or where $f′(x)$ does not exist, provided the value is in the domain of the original function.

The Second Derivative Test attempts to classify these points by evaluating the sign of $f″(c)$, but this method relies heavily on the existence and nonzero value of the second derivative. When those conditions fail, the test becomes inconclusive.

Why the Second Derivative May Be Inconclusive

There are two primary reasons this loss of reliability occurs:

1. The Second Derivative Equals Zero

If $f′(c)=0$ and $f″(c)=0$, the second derivative provides no curvature information. A zero second derivative means the graph may be flattening, but that flattening could correspond to many different shapes.

Situations that can produce this outcome include:

• Higher-order flatness, where several derivatives vanish before curvature appears.

• Horizontal points of inflection, where the graph flattens but does not change direction.

• Symmetric or balanced behavior, where competing tendencies cancel out at the point.

This situation forces us to avoid relying on second-derivative curvature cues because they cannot distinguish between a minimum, maximum, or neither.

If f′(c)=0 and f″(c)=0, the second derivative provides no curvature information at x=c, so the test cannot tell whether c is a max, min, or neither.

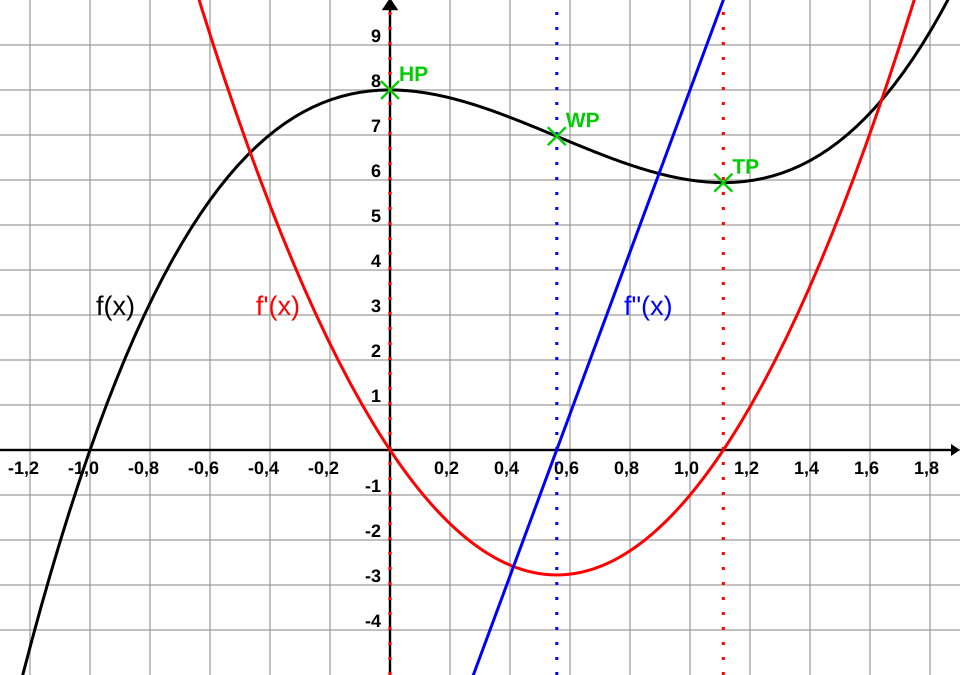
A cubic function is plotted in black with its first derivative shown in red and second derivative in blue. The labeled local maximum, local minimum, and inflection point illustrate how $f''(c)=0$ may correspond to different behaviors. This demonstrates why the Second Derivative Test is inconclusive when both $f'(c)=0$ and $f''(c)=0$. Source.

2. The Second Derivative Does Not Exist

If $f′(c)=0$ but $f″(c)$ does not exist, the Second Derivative Test cannot be applied. This occurs when:

• The graph has a sharp flattening or cusp-like behavior in $f′(x)$.

• The function’s rate of change changes abruptly, preventing differentiation.

• The curvature is undefined or infinite.

Even though $f′(c)=0$ shows a horizontal tangent line, the missing curvature information makes the standard test unsuitable.

Revisiting the Structure of the Second Derivative Test

The essence of the test depends on evaluating the concavity at a critical point. Concavity for AP Calculus AB purposes relies on the sign of the second derivative.

Normal sentence here to provide explanatory continuity. When either issue arises, no reliable curvature-based classification can occur, which is exactly what makes the test inconclusive.

How to Proceed After the Test Fails

Once students recognize that the Second Derivative Test breaks down, they must shift to a different method. The AP specification emphasizes the First Derivative Test as the primary backup strategy.

Using the First Derivative Test After Inconclusiveness

The First Derivative Test analyzes sign changes in the first derivative around the critical point and is more broadly applicable because it does not require smoothness beyond the existence of $f′(x)$ on intervals around the point.

To apply this test:

• Identify the critical point where the Second Derivative Test failed.

• Determine intervals directly to the left and right of that point.

• Evaluate the sign of $f′(x)$ on each interval.

• Interpret the change (or lack of change) to classify behavior.

This process is effective because increasing and decreasing behavior provides direct evidence of local maxima or minima.

Additional Indicators When Needed

When both curvature and sign-chart methods seem unclear, students can turn to additional information, including:

• Local graph behavior, when graphical representations are provided.

• Derivative tables, which summarize the sign of $f′$ across key points.

• Contextual smoothness assumptions, such as knowing the function is polynomial.

However, these are only secondary aids; the primary fallback remains the First Derivative Test.

Why the Inconclusive Case Matters

The inconclusive scenario highlights an important conceptual point in calculus: higher-order derivatives provide information about shape, but they do not always tell the full story. A function may appear flat at a point, yet its behavior on either side determines the actual extremum classification. AP Calculus students must therefore be comfortable switching analytical tools when necessary.

Understanding this limitation strengthens students’ conceptual grasp of derivative-based analysis and reinforces that no single test works universally.

Key Takeaways for AP Students

• The Second Derivative Test can only classify a critical point when $f′(c)=0$ and $f″(c)\neq 0$.

• If $f″(c)=0$ or $f″(c)$ does not exist, curvature information is insufficient.

• In such cases, the First Derivative Test provides the required classification method.

• Recognizing when a method fails is just as important as knowing when it succeeds.

When the Second Derivative Test is inconclusive, we return to the First Derivative Test and analyze sign changes in f′ or use graphs and tables to understand the function’s behavior near c.

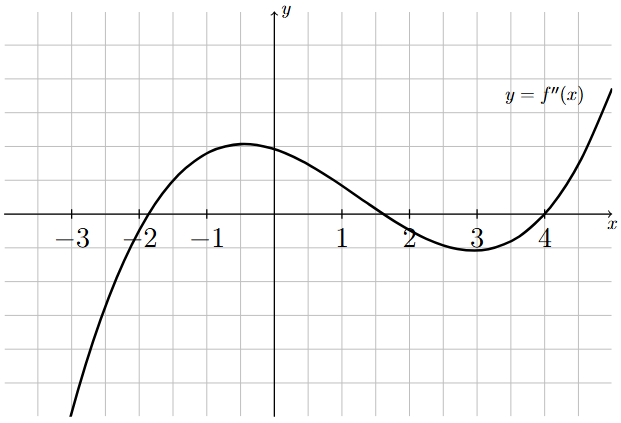
The graph displays a continuous second derivative that touches the $x$-axis at $x=0$ while remaining positive elsewhere. Because $f''(0)=0$ without a change of sign, the Second Derivative Test cannot classify the critical point. Examining $f'(x)$ instead provides the needed information about slope changes to determine the point’s behavior. Source.