AP Syllabus focus:
‘The Second Derivative Test classifies certain critical points: if f′(c)=0 and f″(c)>0, then f has a local minimum at c; if f″(c)<0, then f has a local maximum at c.’
The Second Derivative Test provides a powerful method for classifying certain critical points by examining concavity. It connects the sign of the second derivative to the local behavior of a function.
Understanding the Purpose of the Second Derivative Test
The Second Derivative Test helps determine whether a critical point corresponds to a local minimum, local maximum, or an inconclusive situation requiring another method.

A smooth curve shows local and global maxima and minima clearly labeled. This illustrates how different critical points on one function can represent different types of extrema when . The image contains both absolute and relative extrema, slightly exceeding the syllabus focus but reinforcing conceptual understanding. Source.
This test is particularly useful because it links ideas from differentiation, curvature, and function behavior. It is applied after identifying a critical point where the first derivative equals zero, and it relies on evaluating the concavity at that precise location.
A critical point is any point where a function’s derivative is zero or does not exist, provided the point lies within the domain of the function. This is where important features of the graph, such as peaks or valleys, may occur.
Term: A critical point is an -value in the domain of a function where or does not exist.
Because the Second Derivative Test only works when the first derivative equals zero at the point of interest, the test cannot be applied at points where the derivative fails to exist. A clear understanding of this restriction helps avoid misapplication.
Conditions Required for Applying the Test
Before using the Second Derivative Test, certain conditions must be met. These ensure that the method gives reliable information about the behavior of the graph near the critical point.
Necessary Conditions
The function must be differentiable near the point being tested so that the second derivative is defined in the surrounding region.
There must be a critical point where , since the test relies on substituting this value into the second derivative.
The value of must exist; if it does not, the test cannot be completed.
Because this test depends on concavity, it does not require analyzing intervals around the point unless fails to give conclusive information.
What the Second Derivative Represents
The second derivative gives information about the function’s concavity—how the graph bends. Positive second derivatives indicate that the graph bends upward, while negative second derivatives indicate downward bending.
Term: Concavity describes the direction a graph curves; upward curvature corresponds to positive second derivative values, while downward curvature corresponds to negative second derivative values.
Understanding concavity is essential because local minima typically occur where the graph bends upward, and local maxima occur where it bends downward.
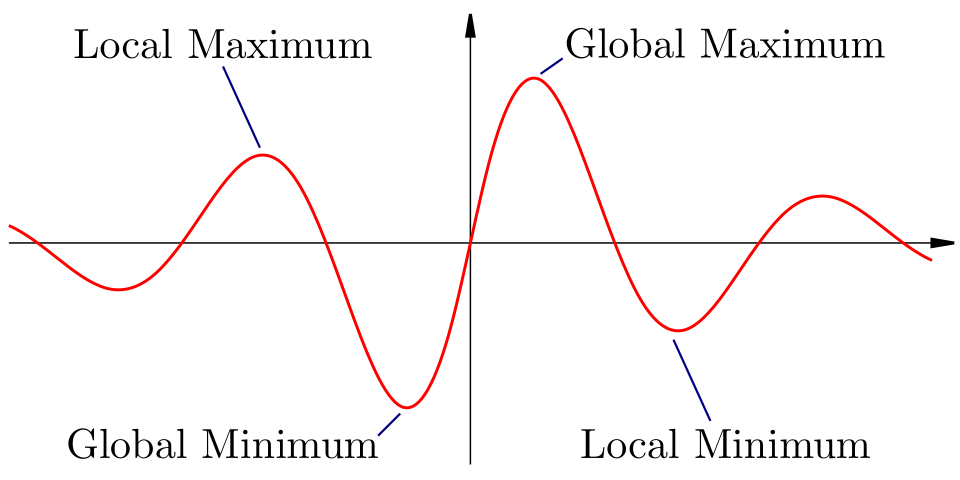
A damped oscillating function displays multiple local and global extrema. This illustrates how changing concavity produces alternating maxima and minima. The inclusion of both global and local extrema provides additional context beyond the syllabus but supports conceptual clarity. Source.
Formal Statement of the Second Derivative Test
The AP specification states: if and , the function has a local minimum at , and if , the function has a local maximum at . This classification method uses curvature to describe how the function behaves immediately around the point.
The Second Derivative Test does not guarantee that every critical point can be evaluated this way. If or does not exist, the test fails to classify the point and another method—often the First Derivative Test—must be used.
= Critical point where the tangent line is horizontal
= Indicates the graph is concave up at
= Indicates the graph is concave down at
This mathematical framework provides a structured pathway from derivative information to conclusions about local behavior.
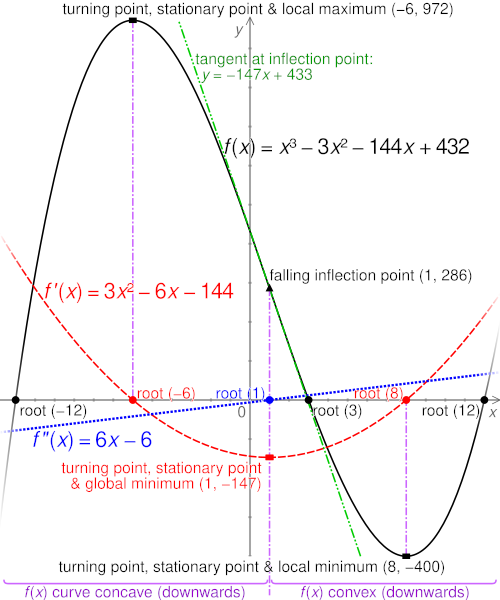
The graph shows a cubic polynomial alongside its first and second derivatives, with marked roots, stationary points, and an inflection point. It demonstrates how corresponds to extrema on the original function while indicates concavity at those points. The image includes detailed labels beyond the syllabus but offers a clear geometric connection between the derivatives and extremum classification. Source.
How the Test Classifies Local Extrema
The Second Derivative Test focuses on three potential outcomes:
1. Identifying Local Minima
If and , the function is concave up at . A graph that curves upward near a horizontal tangent resembles a valley, which means the point represents a local minimum. The upward curvature confirms the point is lower than nearby values.
2. Identifying Local Maxima
If and , the function is concave down at . A graph that curves downward near a horizontal tangent resembles a hilltop. This makes the point a local maximum because it is higher than points immediately surrounding it.
3. When the Test Is Inconclusive
When but or the second derivative does not exist, the test provides no classification. In these situations, the function may have a local extremum, a point of inflection, or no special behavior at all. The analysis must continue using alternative tools such as a sign chart for the first derivative.
Practical Advantages of the Second Derivative Test
The main benefit of the Second Derivative Test is its efficiency. Instead of analyzing intervals for increasing or decreasing behavior, you can quickly plug a critical point into the second derivative:
If positive, classify as a local minimum.
If negative, classify as a local maximum.
If zero or undefined, switch to a different method.
This makes it especially helpful when working with functions whose first derivative is complicated to analyze on intervals. In such cases, evaluating the second derivative at a single point is often much simpler and more direct.
FAQ
The test describes how sharply the function bends near the critical point. A positive second derivative indicates a bowl-shaped curve that opens upward, often meaning the minimum is gently sloped or tightly curved depending on the size of the value.
A negative second derivative indicates a hill-shaped curve opening downward, and the magnitude of the value reflects how steeply the curve bends.
The test works only on the sign of the second derivative, not its magnitude. However, when the value is extremely small, numerical or rounding error may obscure the true sign.
In such cases, it is safer to check the behaviour of the first derivative around the point or analyse the function’s expression more precisely before concluding.
The test assumes the function is smooth enough around the point for curvature arguments to apply. If the first derivative does not exist, the graph may have a cusp or corner, and curvature is not well defined.
Such points cannot be interpreted using concavity alone, so the test is invalid unless the derivative equals zero.
A larger magnitude of the second derivative indicates a sharper curve.
• A large positive second derivative produces a steep, tightly curved minimum.
• A small positive value gives a flatter, more open minimum.
• A large negative value indicates a sharply peaked maximum, while a small negative value suggests a flatter maximum.
Indirectly, yes. A change in the sign of the second derivative on either side of the critical point suggests a transition in concavity.
If the second derivative is positive at the critical point but negative nearby (or vice versa), the concavity shift implies the presence of an inflection point close to, but not at, the critical point itself.
Practice Questions
Question 1 (1–3 marks)
A function g has a critical point at x = 4, where g'(4) = 0. It is known that g''(4) is negative.
(a) State what the Second Derivative Test concludes about the point x = 4.
(b) Explain briefly why this conclusion follows from the value of g''(4).
Question 1 (3 marks total)
(a) 1 mark: States that x = 4 is a local maximum.
(b) 1 mark: States that a negative second derivative indicates the graph is concave down at x = 4.
1 mark: Connects concavity to the conclusion (a concave-down shape at a horizontal tangent gives a maximum).
Question 2 (4–6 marks)
A function f is differentiable on an open interval containing x = 1. You are given that f'(1) = 0 and f''(1) = 7.
(a) Use the Second Derivative Test to determine the nature of the critical point at x = 1.
(b) Give a clear explanation using concavity to justify your answer.
(c) Describe one situation in which the Second Derivative Test would not allow you to classify a critical point, and explain what alternative method could then be used.
Question 2 (6 marks total)
(a) 1 mark: Identifies x = 1 as a local minimum.
1 mark: Uses the fact that f''(1) is positive to support this.
(b) 1 mark: Explains that positive second derivative indicates concave-up behaviour.
1 mark: Relates concavity to the minimum (a concave-up shape with a horizontal tangent produces a minimum).
(c) 1 mark: States a situation such as f''(c) = 0 or f''(c) does not exist.
1 mark: Mentions that another method, such as the First Derivative Test or a sign analysis of f', must then be used.

