Understanding how concavity influences the classification of local extrema is essential in calculus, because it links geometric shape, derivative behavior, and the Second Derivative Test in a unified way.

Concavity as a Tool for Classifying Extrema

Concavity describes how a graph bends, and it plays a key role in determining whether a critical point corresponds to a local maximum, local minimum, or neither. The AP Calculus AB specification emphasizes that local minima appear in regions where the function is concave up, while local maxima appear where the function is concave down. This connection forms the core of the Second Derivative Test and is a powerful tool when the first derivative alone does not immediately reveal the function’s local behavior.

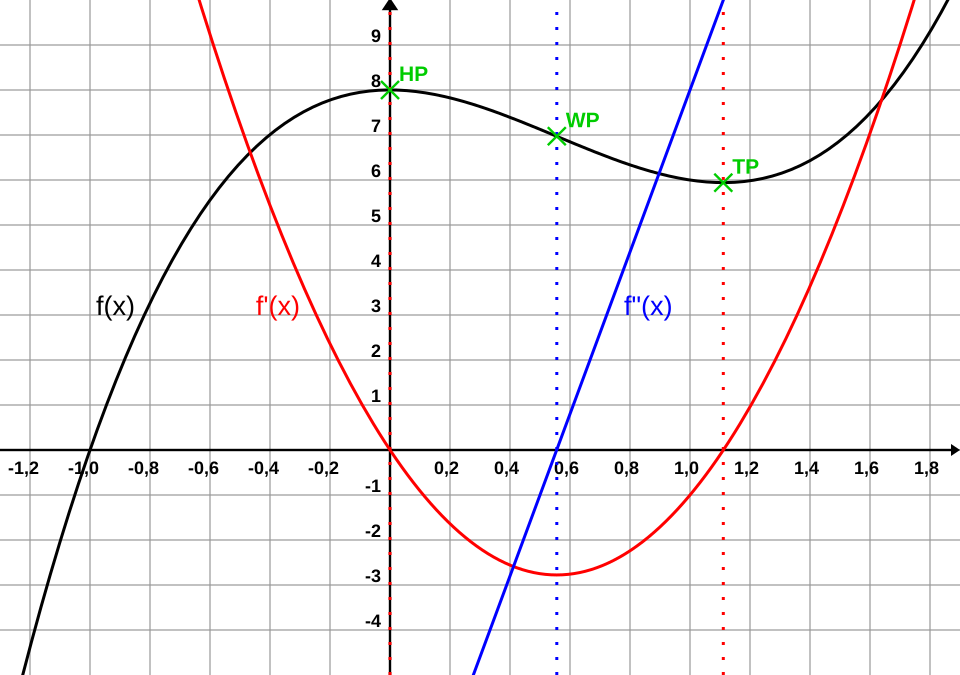
Graph of a cubic function $f(x)=3x^{3}-5x^{2}+8$ with local maximum, local minimum, and an inflection point labeled, accompanied by graphs of $f'(x)$ and $f''(x)$. The sign of $f''(x)$ illustrates where the graph is concave up or concave down, showing why concave-up regions produce local minima and concave-down regions produce local maxima. The inflection point is additional detail beyond this subsubtopic but reinforces how changing concavity relates to extrema. Source.

Definition of Concavity

A sentence explaining: Concavity provides geometric insight, allowing us to interpret how the slopes of tangent lines change around a point of interest.

Interpreting Concave Up and Concave Down Behavior

The sign of the second derivative reflects how the first derivative changes and how the function curves. When the graph is concave up, the function resembles a “cup” that opens upward; when concave down, it resembles a cap or an inverted bowl.

Concave down behavior requires a separate statement, but this description should not immediately follow the equation block.

When the second derivative is negative over an interval, the graph bends downward, meaning slopes are decreasing as x increases.

How Concavity Predicts Local Extrema

The Second Derivative Test relies on evaluating the sign of $f''(x)$ at a critical point—a point where the first derivative is zero or undefined. Concavity determines whether the point represents a maximum or minimum, based on the nature of the curve around it. This relationship comes directly from the AP specification for this subsubtopic, which states that concave-up regions produce local minima, while concave-down regions produce local maxima near the critical point.

The meaning of this definition is crucial because the Second Derivative Test only applies at these critical points, not at arbitrary points on the graph.

Using the Second Derivative Test to Classify Extrema Through Concavity

The Second Derivative Test offers a structured way to determine whether a critical point is a local maximum, a local minimum, or inconclusive.

• At a critical point where $f'(c)=0$, evaluate $f''(c)$ to determine concavity.
• If f''(c)>0, the function is concave up at x = c, and the point corresponds to a local minimum.
• If f''(c)<0, the function is concave down at x = c, resulting in a local maximum.
• If $f''(c)=0$ or does not exist, the Second Derivative Test does not provide a conclusion about local extrema.

These statements illustrate why concavity is central: it informs how slopes behave on each side of the point.

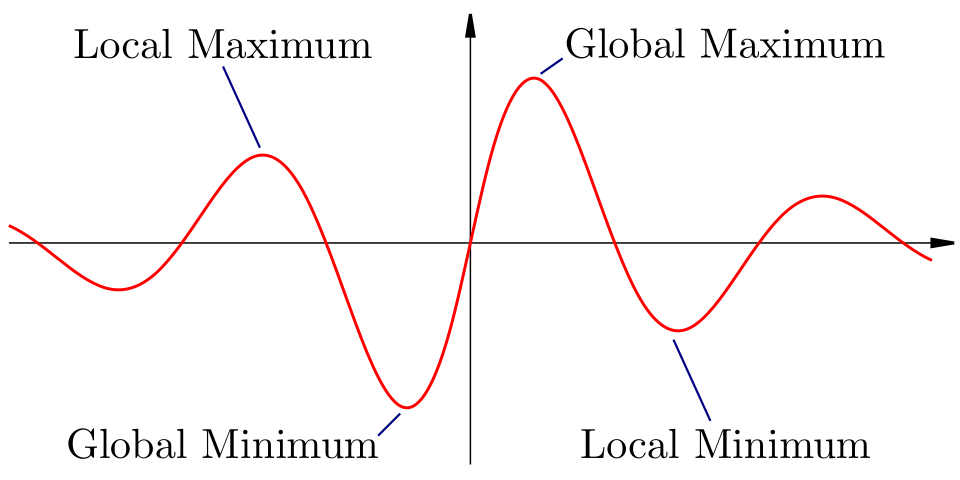
Graph of $f(x)=\sin(x)\exp(-|x/5|)$ with clearly marked local and global maxima and minima. The labeled peaks and valleys highlight where extrema occur and naturally suggest how concavity near each point determines whether it is a maximum or minimum. The distinction between local and global extrema is an additional detail but reinforces precise terminology about extrema. Source.

Geometric Interpretation of the Relationship

Concavity gives a visual interpretation of the Second Derivative Test. Because concave-up graphs open upward, the tangent line at the bottommost point will have zero slope and represent the lowest point locally. Likewise, concave-down graphs open downward, so the tangent line at the topmost point exhibits a local maximum. This geometric view reinforces the specification statement about maxima and minima emerging from concavity patterns.

Limitations Implied by Concavity and the Second Derivative

The Second Derivative Test does not always yield a definitive classification. Even if concavity information is incomplete—such as when $f''(c)=0$—a critical point still exists, but other methods like the First Derivative Test must be used. Concavity remains essential, yet its absence or ambiguity requires shifting strategies.

Why Concavity–Extrema Relationships Matter in Analysis

Connecting concavity to local extrema deepens a student's conceptual understanding of how differential information governs the shape of a function. It highlights that extrema are not isolated algebraic conditions but are tied to how a function curves in its neighborhood. The AP Calculus AB curriculum stresses this relationship so students can analyze graphs, justify behaviors clearly, and understand how derivative tests work together to describe the function’s structure.