Understanding how the first and second derivatives work together provides a powerful framework for analyzing a function’s overall shape, helping us describe its behavior with precision and clarity.

Using f′ and f″ to Understand the Shape of f

How Derivatives Reveal the Structure of a Graph

The behavior of a differentiable function is closely tied to the behavior of its derivatives. The first derivative describes how the function changes, while the second derivative describes how the rate of change itself is changing. Together, they enable us to construct a detailed picture of a function’s rising and falling behavior and its curvature.

When discussing the first derivative, we refer to the derivative of a function that captures its instantaneous rate of change.

The second derivative extends this idea by describing how rapidly the first derivative changes, helping us analyze the graph’s bending and overall shape.

These concepts work together to explain the essential geometric features emphasized in the AP syllabus for this subsubtopic.

Interpreting f′(x): Where the Function Rises or Falls

The first derivative immediately tells us whether the function is increasing or decreasing, which is one of the most fundamental aspects of graph shape. When $f′(x)$ is positive, the graph rises; when $f′(x)$ is negative, the graph falls. This information forms the foundation of any sketch of $f$.
A few core ideas about the first derivative’s relationship to graph behavior include:

• Positive f′(x) indicates an increasing function on the interval.

• Negative f′(x) indicates a decreasing function on the interval.

• Zeros of f′(x) indicate points where the tangent line is horizontal, often corresponding to potential local maxima, local minima, or transition points in the graph’s behavior.

Understanding these features helps us establish the basic rising and falling structure of a graph before refining it with second-derivative information.

Interpreting f″(x): How the Graph Bends

The second derivative adds another layer by describing concavity, which refers to the direction the graph bends. Using f″(x), we can identify where the graph is concave up or concave down, allowing us to sketch the graph with more accuracy and depth.
Important relationships from the second derivative include:

• Positive f″(x) means the graph is concave up, bending upward like a cup.

• Negative f″(x) means the graph is concave down, bending downward like a cap.

• Zeros of f″(x) may correspond to points where concavity changes, known as possible inflection points.

Even without computing exact function values, this information guides the general curvature needed when sketching or describing the function.

When f''(x) > 0 on an interval, the graph of $f$ is concave up there, and when f''(x) < 0, the graph is concave down.

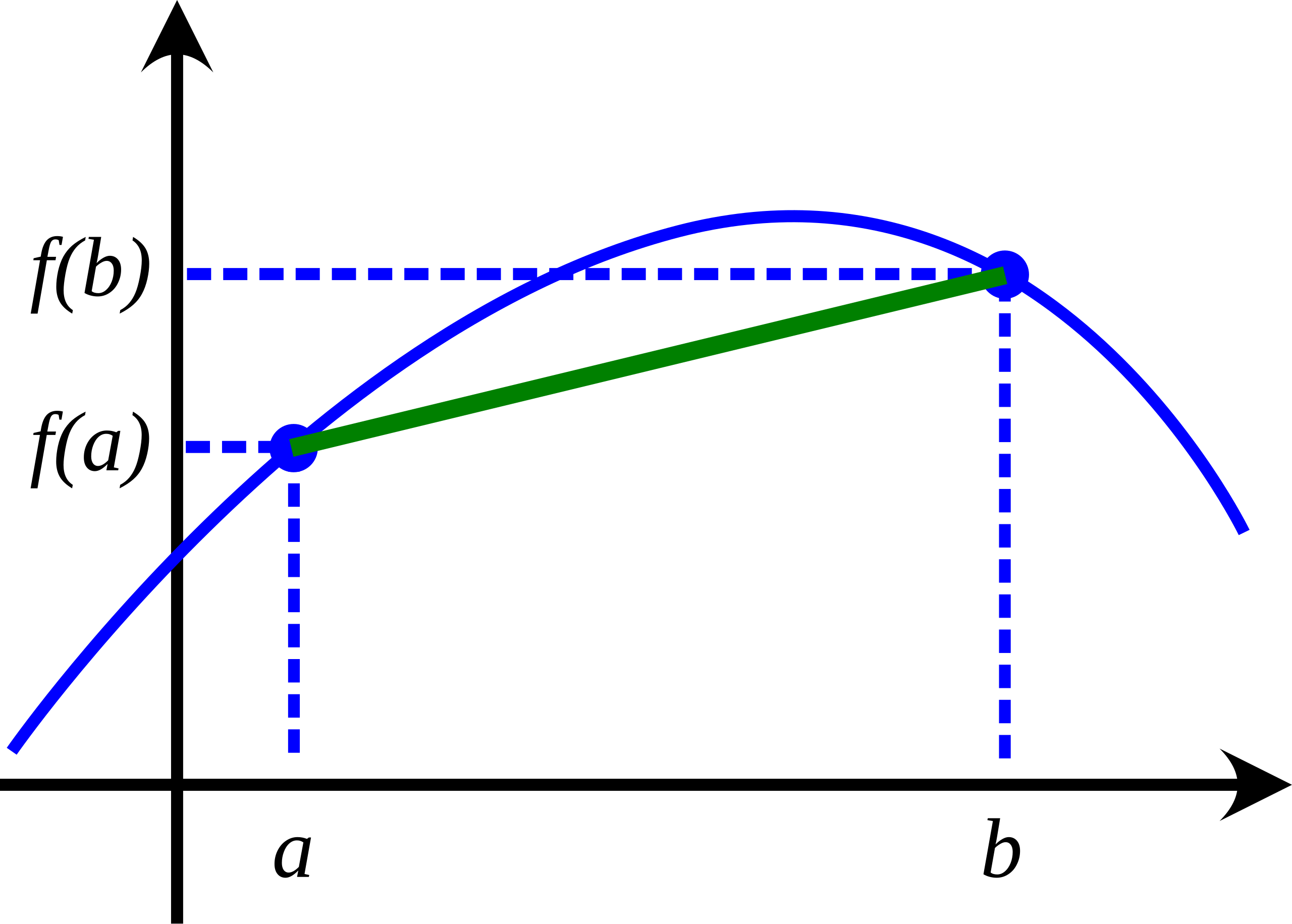
A concave function with its graph bending downward along the interval. The curve illustrates how concavity is determined by the sign of $f''(x)$, showing how the graph bends relative to its chords. This image does not show $f'(x)$ explicitly but supports the idea that $f''(x)$ describes how $f$ bends. Source.

Geometrically, a function is concave up if its graph lies above its tangent lines and concave down if its graph lies below its tangent lines along an interval.

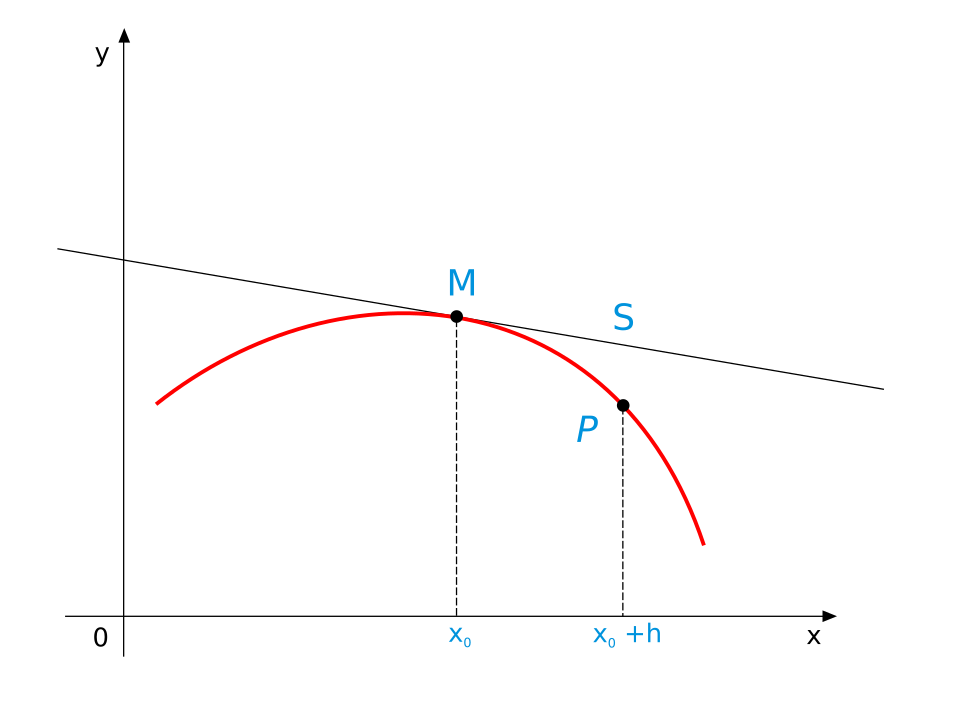
A concave function drawn with a tangent line touching the curve at one point. The diagram emphasizes how the curve consistently bends to one side of the tangent, illustrating the relationship between concavity and tangent-line behavior. The image does not label $f'(x)$ or $f''(x)$ but provides a geometric foundation for understanding how changes in $f'$ shape the graph. Source.

Combining f′ and f″ for a Full Picture of Behavior

Using both derivatives together is essential for understanding the overall shape of the graph. The interplay between the sign of the first derivative and the sign of the second derivative sharpens our description of behavior on any given interval.
Key combinations include:

• f′(x) > 0 and f″(x) > 0: The function is increasing and concave up, producing a shape that rises with an accelerating slope.

• f′(x) > 0 and f″(x) < 0: The function is increasing but concave down, rising more slowly as slopes decrease.

• f′(x) < 0 and f″(x) > 0: The function is decreasing but concave up, approaching a flatter slope as it descends.

• f′(x) < 0 and f″(x) < 0: The function is decreasing and concave down, descending with an increasingly steep slope.

These pairings transform the derivative information into a graphical interpretation that directly influences how the function is shaped on each interval.

Combining the signs of $f'(x)$ and $f''(x)$ lets us distinguish four basic local shapes: rising–concave-up, rising–concave-down, falling–concave-up, and falling–concave-down.

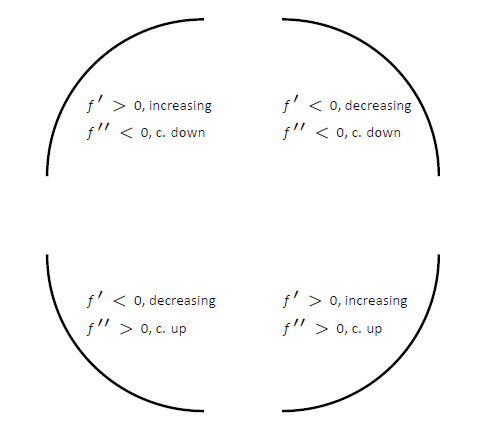
A four-panel diagram illustrating the combinations of increasing/decreasing behavior with concave up/down curvature. Each panel pairs the graph of $f$ with information about $f'$ and $f''$, highlighting how the signs of the derivatives control local shape. The figure includes an explanatory label describing the four concavity–monotonicity interactions, which aligns with AP-level expectations. Source.

Identifying Key Points with the Help of Both Derivatives

Certain important features of a graph—such as peaks, valleys, and changes in curvature—can only be fully understood by analyzing the derivatives together.
Some essential categories include:

• Critical points occur where $f′(x) = 0$ or where $f′(x)$ does not exist. These points are candidates for local maxima or minima.

• Points of inflection occur where concavity changes, typically where $f″(x) = 0$ and the sign of $f″(x)$ switches.

• Transition points mark boundaries between intervals of different behaviors, such as changing from increasing to decreasing or from concave up to concave down.

These features, powered by information from both derivatives, allow us to refine a graph sketch beyond the simple placement of plotted points.

Applying Derivative Information to Sketch the Graph of f

Once we understand how f′ and f″ behave, we can translate this information into an accurate and meaningful sketch of the function. While we do not compute values here, the process relies on organizing derivative information systematically:

• Note intervals of increasing and decreasing using the sign of f′(x).

• Identify candidate maxima and minima using zeros of f′(x).

• Determine concavity on intervals using the sign of f″(x).

• Locate potential inflection points by finding where f″(x) equals zero and changes sign.

• Combine all findings to construct the qualitative shape of f, ensuring that rising/falling and concavity behaviors align correctly.

Through this coordinated use of f′ and f″, students gain the ability to understand and describe the shape of a function in a way that is consistent, articulate, and aligned with the expectations of AP Calculus AB.