When sketching f from a given graph of f′, students rely on derivative information to reconstruct how the original function behaves, changes direction, and forms its essential geometric features.

Understanding the Goal When Sketching f from f′

Interpreting the graph of f′(x) allows us to infer the complete qualitative behavior of the original function f(x). Because the derivative encodes rates of change, the vertical placement of f′ relative to the x-axis tells us whether f rises or falls, while the points where f′ touches or crosses the axis identify where the tangent slope of f is horizontal. These observations lead to a sketch that accurately reflects the structure, shape, and transitions of f.

Heading 2

Identifying Increasing and Decreasing Behavior from f′

The graph of f′ serves as a guide to the monotonicity of f, and reading it correctly is essential to producing an accurate sketch of the original function. The values of the derivative provide immediate insight into the directional behavior of the graph.

Heading 3

Using the Sign of the First Derivative
The sign of f′(x) determines whether f(x) is moving upward or downward. When f′ lies above the x-axis, the rate of change is positive, and f is increasing; when f′ lies below the x-axis, the rate of change is negative, and f is decreasing.

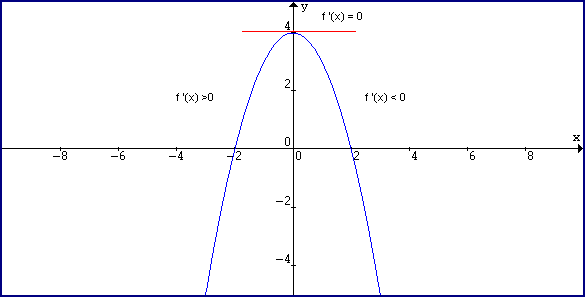
This diagram shows a parabola with tangent lines that have positive, zero, and negative slope at different points. It illustrates how the sign of $f'(x)$ determines whether $f$ rises, levels off, or falls. The slopes shown visually match the rules used when interpreting derivative sign. Source.

A normal sentence must appear here, so the discussion can continue before another definition or equation appears.

Learning to read these signs efficiently equips students to make confident predictions about how f behaves, even without an explicit formula.

Heading 3

Practical Indicators from the Graph of f′
When studying the derivative graph, students should focus on several strategic features:

• Intervals where f′ > 0: These correspond to rising sections of f.

• Intervals where f′ < 0: These correspond to falling sections of f.

• Where f′ = 0: These indicate possible horizontal tangents of f, and therefore possible local extrema.

• Sharp corners or undefined points of f′: These may suggest special behavior, although classification may require sharper analysis.

Understanding these indicators forms the foundation for recreating the broader structure of f.

Heading 2

Locating Key Features: Horizontal Tangents and Critical Behavior

The next major task in sketching f is pinpointing horizontal tangents and recognizing how f′ indicates changes in shape or turning points.

Heading 3

Identifying Roots of f′ and Their Significance
Points where f′ crosses or touches the x-axis are particularly significant because they correspond to locations on f where the slope is zero.

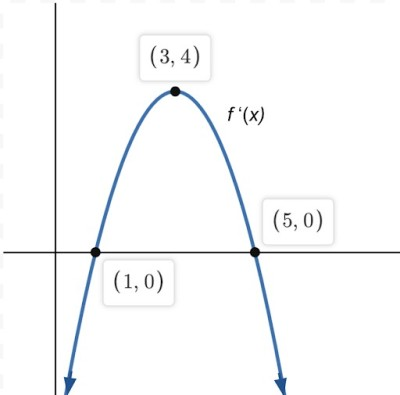
This graph shows $f'(x)$ as a parabola that crosses the x-axis twice, marking the x-values where $f$ has horizontal tangents. The sign of $f'(x)$ above and below the axis determines where $f$ is increasing or decreasing. The figure cleanly demonstrates how zeros of the derivative guide the structure of the sketch of $f$. Source.

These critical points are structural anchors that shape the curve of f, even though not all of them represent maxima or minima.

Heading 2

Building the Sketch of f Using the Behavior of f′

Once the student understands the sign changes, critical points, and slopes suggested by the derivative, sketching f becomes a systematic process.

Heading 3

Step-by-Step Strategy for Sketching
A clear approach ensures that the resulting sketch reflects all essential features:

• Start by marking all x-values where f′ = 0. These mark potential horizontal tangents on f.

• Identify where f′ is positive and negative to organize increasing and decreasing intervals.

• Observe the steepness of f′. A larger magnitude of f′ corresponds to a steeper incline or decline in f.

• Check transitions across roots or special points. Sign changes in f′ imply direction changes in f.

These coordinated observations create a reliable mental map for the appearance of f.

Heading 3

Understanding Changes in Slope Magnitude
Even though the primary focus is the sign of f′, the height of the graph of f′ above or below the x-axis suggests how rapidly f is rising or falling. Higher positive values correspond to quicker upward growth, and larger negative values correspond to faster downward movement. Recognizing these nuances helps produce a more accurate and natural sketch.

Heading 2

Connecting the Geometry of f′ to the Shape of f

Heading 3

Synthesizing Information into a Coherent Sketch
To create a faithful representation of f, students must continuously relate local information from f′ to the emerging global shape of f.

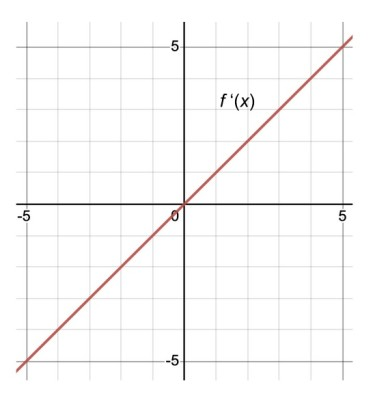
This overlaid plot shows $f(x)$ and $f'(x)$ together so their key features align visually. Where $f'(x)$ is positive, $f$ rises; where it is negative, $f$ falls, and zeros of $f'(x)$ match the turning points of $f$. The figure reinforces how each portion of the sketch of $f$ is determined by interpreting the behavior of $f'(x)$. Source.

Heading 3

The Role of Qualitative Judgment
Finally, constructing f from the graph of f′ calls for thoughtful interpretation, not mechanical plotting. Students must integrate derivative information with geometric reasoning, ensuring that each segment of the graph aligns with the changes indicated by f′.