AP Syllabus focus:
‘Key features such as increasing or decreasing intervals and local extrema of f can be identified by examining where f′ is positive, negative, or zero.’
Increasing and decreasing behavior, along with local extrema, can be determined by analyzing the derivative’s sign and key points where it equals zero, offering a powerful lens into function behavior.
Understanding the Relationship Between f and f′
The connection between a function f and its first derivative f′ is fundamental in calculus because the derivative encodes information about the instantaneous rate of change of f, and by interpreting its sign and zeros, we can infer when f rises, falls, or reaches turning points.
This figure shows a function plotted on a coordinate plane together with line segments that represent slopes at various points, visually emphasizing the derivative as a local rate of change. Labels and slope markings illustrate how different tangent lines correspond to different derivative values along the curve. Some fine-grained symbolic details extend beyond this subsubtopic but remain conceptually consistent with AP Calculus AB. Source.
The Role of the Derivative in Describing Behavior
The derivative f′ provides a direct method for assessing how f behaves on intervals. When we discuss whether a function is increasing or decreasing, we rely on the sign of f′.
Increasing Function: A function is increasing on an interval if, for any two points in that interval, the second function value is greater than the first.
When this idea is paired with derivative analysis, we obtain one of the most important relationships in differential calculus:
Decreasing Function: A function is decreasing on an interval if later function values are smaller than earlier ones in that same interval.
Between these two definitions lies the central insight: the sign of f′ determines whether f is increasing or decreasing.
Using f′ to Identify Increasing and Decreasing Intervals
When the derivative is interpreted graphically, numerically, or algebraically, its sign directly reveals how the original function behaves.
Positive and Negative Values of f′
At the heart of this subsubtopic is the idea that:
If f′(x) > 0, then f is increasing at that point.
If f′(x) < 0, then f is decreasing at that point.
If f′(x) = 0, the function may have a horizontal tangent, and these points are candidates for local maxima or minima.
This relationship allows us to interpret graphs of f′ as powerful diagnostic tools for understanding f.
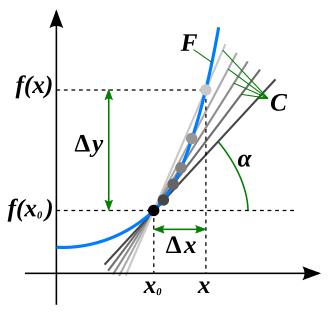
This image presents the graph of a function on a coordinate plane, showing how the output varies as the input changes. It reinforces the idea that the derivative captures changes in slope, enabling identification of increasing and decreasing behavior. Some limit-style notation present in the figure exceeds this subsubtopic but remains aligned with derivative concepts used in AP Calculus AB. Source.
Key Observations from the Sign of the Derivative
The following points illustrate how the derivative's behavior leads to clear conclusions about the original function:
A portion of the graph of f′ lying above the x-axis indicates that f is rising on that interval.
A portion of the graph of f′ lying below the x-axis indicates that f is falling on that interval.
A point where f′ crosses or touches the x-axis indicates a location where the slope of f is zero.
This is why the sign of f′ is one of the core tools for analyzing behavior in AP Calculus AB.
Using Zeros of f′ to Identify Local Extrema
Beyond intervals of monotonicity, the derivative provides vital information about the local extrema of f.
Local Maxima and Minima from the Behavior of f′
A local extremum occurs where the function achieves a highest or lowest value relative to nearby points.
Local Extremum: A point where a function reaches a local maximum or minimum value within a surrounding interval.
While this definition identifies where extrema might occur, f′ reveals how the function behaves around these points.
How the Sign of f′ Reveals Extrema
When examining the derivative around a point where f′ = 0, the pattern of sign changes communicates whether the function forms a peak, a valley, or neither.
Positive → Negative: f transitions from rising to falling, indicating a local maximum.
Negative → Positive: f transitions from falling to rising, indicating a local minimum.
No sign change: The function does not form a local extremum there.
These conclusions arise entirely from studying the derivative, reflecting the AP specification’s focus on understanding key features via f′.
Visual Interpretation: Linking Graphs of f and f′
Much of the insight provided by f′ becomes clearer when graphically interpreted.
Graph of f′ as a Window into the Behavior of f
By observing where the derivative lies above or below the x-axis, we can visually sketch where the original function increases or decreases. Important connections include:
Peaks in f correspond to places where f′ changes from positive to negative.
Valleys in f correspond to places where f′ changes from negative to positive.
Flat spots or plateaus in f correspond to points where f′ touches or crosses the x-axis.
Bullet-pointed observations can help students internalize the relationships:
Horizontal tangents of f ↔ zeros of f′
Increasing intervals of f ↔ positive values of f′
Decreasing intervals of f ↔ negative values of f′
Extrema of f ↔ sign changes of f′
These connections reinforce the syllabus emphasis on using f′ to identify increasing or decreasing intervals and to locate local extrema.
Integrating Graphical and Algebraic Views
Recognizing how algebraic results from derivative calculations align with visual interpretations deepens conceptual understanding. Students should consistently connect:
The sign of f′
The behavior of f
The shape and features of both graphs
This integrated viewpoint enables accurate qualitative analysis of functions using the derivative alone.
How f′ Encodes the Essential Features of f
Everything in this subsubtopic centers on a single idea: the derivative summarizes how the original function behaves. By studying f′, students gain access to a precise and efficient method for identifying:
Where the function increases
Where it decreases
Where its slope is zero
Where it may have local maxima or minima
These relationships make derivatives an indispensable analytical tool in AP Calculus AB, aligning directly with the specification’s emphasis on identifying key features of f through f′.
FAQ
Look at the slope of the tangent line you would draw at various points on the graph of f.
If the graph slopes upwards as you move left to right, then f′ is positive.
If it slopes downwards, then f′ is negative.
Where the graph becomes flat, f′ is close to zero.
This allows a qualitative prediction of the derivative’s sign even before computing or graphing f′.
Plotted points only show function values and can miss subtle changes in slope between them.
In contrast, the derivative describes behaviour continuously across the entire interval.
This prevents misinterpretation caused by sparse data points, rounding, or scaling.
Using f′ is therefore a more precise method for identifying monotonic behaviour.
Yes. A function may remain increasing even if f′ equals zero at isolated points, provided f′ never becomes negative.
This occurs in functions with stretches where the slope briefly levels off.
Only when f′ becomes negative does the function begin decreasing.
Thus, zeros of f′ are not, by themselves, evidence of a change in behaviour.
If f′ is near zero but consistently positive or consistently negative, the function changes very slowly.
The function will still be increasing or decreasing, but at a very gentle rate.
Such behaviour often produces nearly horizontal portions of the graph.
This can occur in functions that flatten out without forming an extremum.
Certain features of f′ make an extremum improbable:
• Long stretches where f′ never approaches zero.
• Sharp transitions where f′ jumps from one positive value to another but never crosses zero.
• Regions where f′ oscillates but remains strictly above or below the axis.
In these cases, the function’s slope never becomes flat, so turning points are unlikely.
Practice Questions
(1–3 marks)
The graph of the derivative f′ of a differentiable function f is shown to be entirely above the x-axis on the interval 0 < x < 5. What can be concluded about the behaviour of f on this interval? Explain briefly.
(1–3 marks)
• 1 mark: States that f is increasing on 0 < x < 5.
• 1 mark: Explains that this is because f′ is positive on the entire interval.
• 1 additional mark (optional) for noting that no information about maxima or minima can be inferred without f′ crossing or touching the x-axis.
(4–6 marks)
The derivative of a function f is given by f′(x) = (x − 2)(x + 1).
(a) Determine the intervals on which f is increasing and the intervals on which it is decreasing.
(b) Hence determine the x-values at which f has a local maximum or a local minimum, giving reasons based on the sign of f′.
(4–6 marks)
(a)
• 1 mark: Identifies critical points at x = −1 and x = 2.
• 1 mark: Determines the sign of f′ on each interval (e.g., f′ positive on x < −1, negative on −1 < x < 2, positive on x > 2).
• 1 mark: Concludes intervals: f increasing on (−∞, −1) and (2, ∞); f decreasing on (−1, 2).
(b)
• 1 mark: States that f has a local maximum at x = −1 because f′ changes from positive to negative.
• 1 mark: States that f has a local minimum at x = 2 because f′ changes from negative to positive.

