AP Calculus AB integration problems require quickly identifying integrand structure to select a suitable antidifferentiation technique. This section trains you to categorize integrands efficiently.

Classifying Integrands by Their Algebraic and Functional Structure

Recognizing the type of integrand is a critical skill because each form aligns naturally with a particular antidifferentiation strategy.

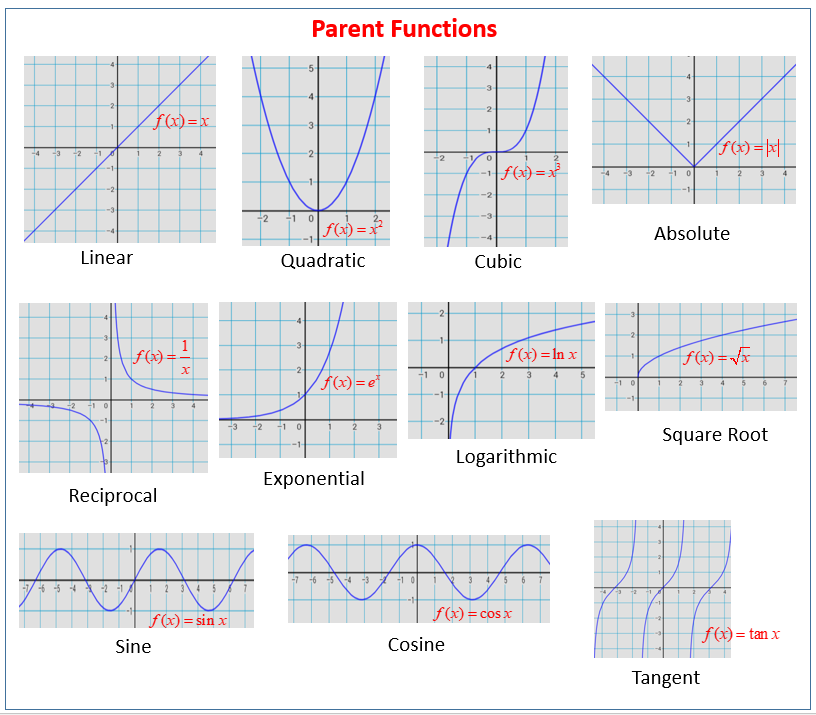
Graphs of several parent functions illustrate how different function families have distinct shapes and behaviors. Recognizing these families helps reinforce the classification of integrands by type. Some functions shown (e.g., logarithmic and certain trigonometric curves) extend beyond the minimal syllabus needs but still strengthen structural recognition skills. Source.

…because each form aligns naturally with a particular antidifferentiation strategy. When students can match structure to method, integration becomes a process of logical selection rather than guesswork.

Why Classification Matters

An integrand’s features often reveal whether basic rules, substitution, or algebraic rearrangements will produce the most direct path to an antiderivative. Observing the form of expressions, the presence of composition, and relationships between factors helps determine the correct approach.

Polynomial and Power-Type Integrands

Polynomial expressions are typically the simplest to classify because they align directly with the standard power rule for antiderivatives.

Polynomial integrands frequently appear in expanded form, making them easy to integrate term by term. When polynomials multiply other expressions, however, classification requires determining whether substitution or algebraic simplification is more suitable.

Exponential and Logarithmic Integrands

Exponential and logarithmic expressions often suggest basic rules or straightforward substitutions. For instance, integrands built around $e^x$ or constant-base exponentials typically integrate directly unless multiplied by additional functions requiring further consideration.

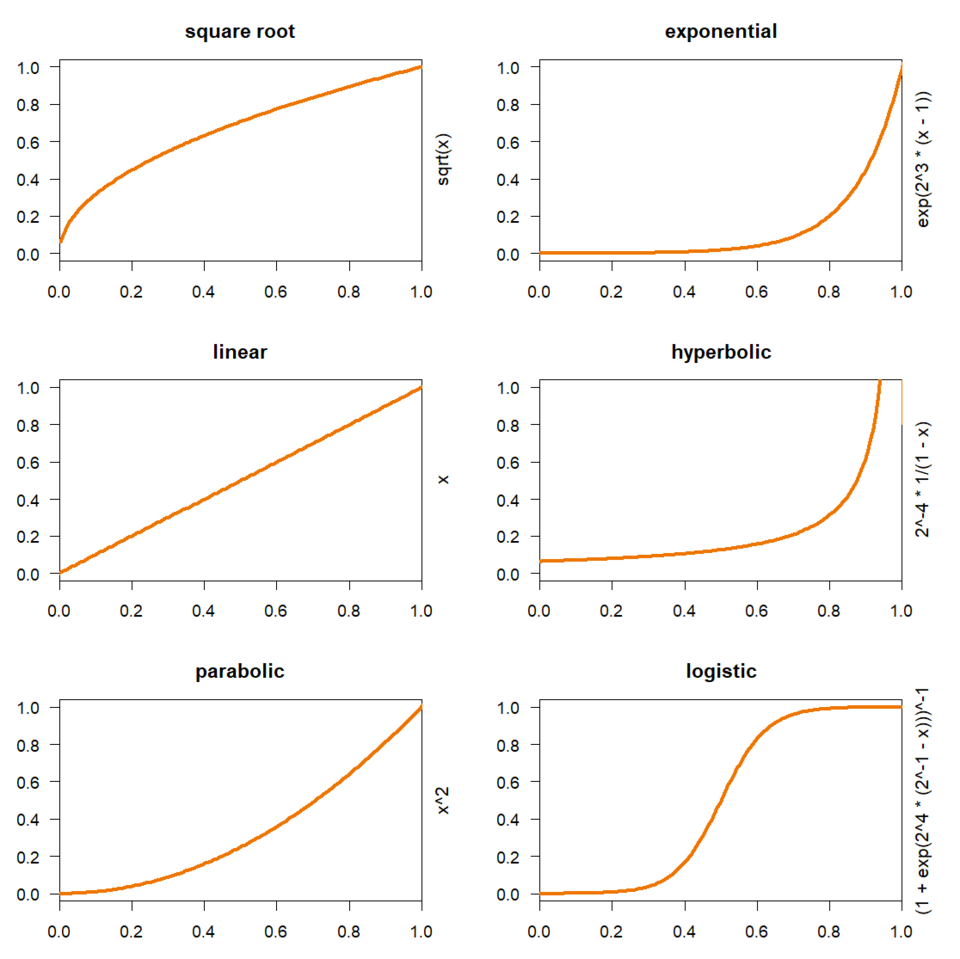
This diagram compares multiple monotonic functions, highlighting differences in curvature and growth rate across linear, polynomial-like, and faster-growing functional types. Such contrasts reinforce classification of integrands by functional behavior. Some labeled curves extend slightly beyond AP Calculus AB requirements but still support conceptual understanding of growth families. Source.

Because exponentials frequently appear in compositions, it is essential to inspect whether the inner function and its derivative appear in a recognizable relationship.

Trigonometric Integrands and Structural Patterns

Trigonometric integrands require special attention because certain pattern forms immediately suggest known antiderivatives or substitutions. Determining whether an expression resembles a standard trigonometric derivative helps guide the selection of technique.

Common structural cues include:

• Products like trig × derivative of trig, indicating substitution.

• Squared trigonometric forms that resemble identities.

• Quotients matching derivatives of inverse trigonometric functions.

Identifying Integrands Suited to Substitution

A function may appear complicated, but the presence of an inner function and its related derivative often signals that substitution is the most efficient antidifferentiation method.

To classify integrands for substitution:

• Look for nested expressions such as radicals, powers, or exponentials applied to nontrivial inner functions.

• Confirm that a matching derivative or proportional expression is present.

This observational step prevents unnecessary algebra and improves accuracy.

Integrands Requiring Algebraic Rearrangement

When an integrand does not initially resemble any basic type, algebraic restructuring may reveal an appropriate technique. Classification therefore includes recognizing when an expression must be transformed before integration.

Situations requiring rearrangement include:

• Rational functions where the numerator is of equal or higher degree than the denominator (suggesting long division).

• Quadratic expressions inside radicals or denominators that benefit from completing the square.

• Factored forms that separate into simpler pieces for term-by-term integration.

Recognizing the need for rearrangement helps prevent misapplication of substitution or basic rules.

Rational Functions and Their Indicators

Rational integrands comprise ratios of polynomials. Classification within this category focuses on determining whether:

• The integrand is already in a form suited to basic rules,

• Long division is required to simplify,

• A denominator suggests a known antiderivative structure, or

• The expression resembles forms associated with inverse trigonometric derivatives.

Because rational functions exhibit wide structural variety, careful inspection of degrees, factoring, and symmetry is essential.

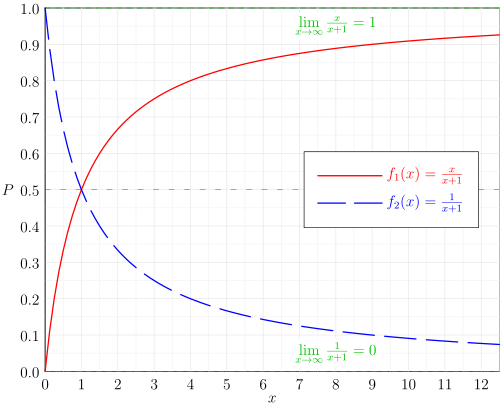
The graph juxtaposes two rational functions that share a denominator but differ in long-run behavior, illustrating how structure influences classification. Visible horizontal asymptotes and limit statements highlight key features of rational integrands. Some limit annotations provide additional insight beyond the immediate syllabus scope but strengthen conceptual interpretation. Source.

Recognizing Mixed-Type Integrands

Some expressions combine multiple function families, such as exponentials multiplied by polynomials or trigonometric factors paired with algebraic expressions. These “mixed-type” integrands often require identifying which component guides the technique selection.

Key indicators include:

• A polynomial factor multiplying a function with a recognizable derivative structure.

• A trigonometric factor aligning with a substitution target.

• A composition where one part clearly behaves as a derivative of another.

Mixed integrands challenge students to classify by relationship, not just by function type.

Strategic Classification as a Repeated Process

Effective classification is not a single-step judgment but a layered evaluation. Students should:

• Scan the integrand for recognizable basic-rule forms.

• Check for composition, noting relationships between functions and derivatives.

• Evaluate algebraic complexity, determining whether simplification is necessary.

• Confirm suitability of suspected techniques by matching structure to known antiderivative patterns.

This systematic approach builds confidence and supports efficient integration throughout AP Calculus AB.