AP Syllabus focus:
‘Practice selecting and justifying a complete solution strategy for an integral, drawing on all available antidifferentiation techniques learned in this unit.’
Effective integration strategy requires identifying structural patterns in an integrand, selecting the most efficient method, and justifying each choice using established antidifferentiation techniques developed throughout AP Calculus AB.
Strategy Review for Antiderivatives and Definite Integrals
A successful approach to integration begins with analyzing the form of the integrand and the context of the problem. Students must make deliberate choices among available tools, ensuring each technique fits the functional structure presented. This subsubtopic emphasizes the reasoning process behind selecting an integration method, not merely applying formulas.
Recognizing Structural Cues in an Integrand
The first step in choosing a strategy is assessing recognizable algebraic or functional features. Look for patterns that hint at a known method. Students should carefully analyze whether the integrand resembles a basic rule, a composite function, a product of functions, a rational expression, or an expression requiring algebraic simplification. The choice of method should emerge naturally from this structural assessment.
Integrand Structure: The identifiable algebraic or functional pattern within an expression that suggests an appropriate antidifferentiation technique.
When structural cues are unclear, begin by attempting the simplest possible method; only escalate to more complex techniques when necessary.
Applying Basic Antiderivative Rules When Appropriate
Many integrals can be evaluated directly using familiar rules for powers, exponentials, and trigonometric functions. Students should always check first whether the integrand already appears in a standard form before considering alternative methods. Misidentifying a simple integrand often leads to unnecessary complexity. Trusting the catalog of known formulas is fundamental to efficient strategy selection.
Identifying When to Use Substitution
Whenever an integrand contains a composite function or a function paired with its derivative, substitution becomes a powerful method, allowing a complicated expression to be rewritten in simpler terms. The presence of an inner function and its differential counterpart is a strong indicator that substitution is the most efficient technique available.
Substitution (u-substitution): A method that rewrites an integral by introducing a new variable to simplify a composite structure, effectively reversing the chain rule.
This technique is especially effective when the integrand’s complexity arises from nested functions rather than products or rational expressions.
Deciding When Integration by Parts Is Necessary
If the integrand is built from a product of two functions whose differentiation and integration create a beneficial pairing, integration by parts becomes a natural choice. This method is most helpful when one factor simplifies upon differentiation while the other remains integrable.
= Function chosen to differentiate
= Function chosen to integrate
This formula is essential when substitution cannot simplify the expression sufficiently, particularly with logarithmic or inverse trigonometric factors.
This diagram presents the identity for integration by parts, visually emphasizing how a product of functions can be reorganized into a simpler integral. It highlights the roles of , , , and , supporting strategic decisions in choosing this method. Source.
Choosing Algebraic Techniques Before Integrating
Sometimes an integrand resists direct antidifferentiation until it has been rewritten using algebraic methods such as factoring, long division, or completing the square. These techniques transform difficult expressions into forms suitable for standard rules or substitutions.
Algebraic Rearrangement: Any manipulation of an integrand—including factoring, expanding, or rewriting forms—to make the expression more amenable to integration.
Using these rearrangements strategically prevents errors and ensures more efficient integration.
Decomposing Rational Functions When Needed
When the integrand is a rational function with a denominator that factors linearly, partial fraction decomposition may be the most appropriate choice. This method breaks a complex fraction into simpler components that match known antiderivatives. Recognizing when decomposition is possible is crucial for selecting the correct approach.
Strategies for Definite Integrals
For definite integrals, choosing the correct method also involves deciding whether to manipulate the integrand or to exploit integral properties. Consider the following when selecting a strategy:
- Whether substitution simplifies the bounds.
- Whether an algebraic rewrite creates symmetry that makes evaluation easier.
- Whether integration by parts is necessary for products that do not simplify directly.
- Whether partial fractions convert the problem into simpler integrals.
- Whether known geometric areas replace the need for computation.
Students should also recall that the structure of a definite integral may allow a faster approach than computing an antiderivative.
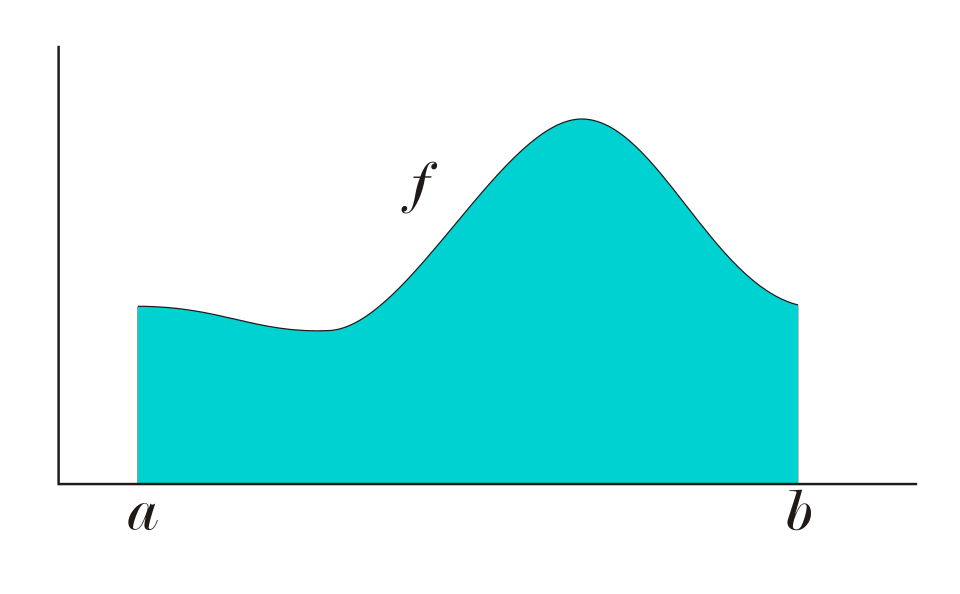
This graph illustrates a function with the area under the curve between and representing the definite integral . It emphasizes that a definite integral may be evaluated using geometric reasoning rather than symbolic antidifferentiation when appropriate. Source.
Justifying Strategic Choices
Beyond selecting a method, this subsubtopic requires articulating why a chosen technique is appropriate. Justification should reference the integrand’s structure:
- Choose basic rules when the integrand matches a memorized formula.
- Choose substitution when a chain-rule relationship is visible.
- Choose integration by parts when a product suggests beneficial differentiation.
- Choose algebraic rearrangement when simplification clarifies the structure.
- Choose partial fractions when rational functions separate cleanly into linear components.
Reasoned explanation demonstrates not only procedural knowledge but also conceptual understanding, aligning with AP expectations for strategic mathematical thinking.
FAQ
Look for expressions that are not easily matched to known antiderivative forms, such as rational functions with higher-degree numerators or nested algebraic terms.
If simplification reveals a clearer structure (for example, a sum of simpler terms), that often signals the correct method.
Common indicators include:
• A numerator and denominator of similar degree.
• Polynomials that factor neatly.
• Expressions that resemble a standard derivative once expanded or rearranged.
Many students choose a familiar method rather than the one most suited to the integrand. This often happens with substitution and integration by parts.
A better approach is to pause and assess the integrand’s structure before acting.
Key avoidance tips:
• Do not apply substitution automatically when you see brackets.
• Do not use integration by parts unless a clear product structure benefits from it.
• Always consider whether rewriting the expression first would simplify the work.
A strong justification links a feature of the integrand to the method chosen.
Examples of clear justification include:
• Identifying that a factor simplifies upon differentiation (supporting integration by parts).
• Noting the presence of an inner function and its derivative (supporting substitution).
• Explaining that algebraic simplification exposes standard antiderivative forms.
Use concise phrasing that highlights structural recognition rather than describing the full computational process.
Begin by applying the simplest possible analysis:
• Expand or factor the expression to reveal patterns.
• Check whether any part resembles a known derivative.
• Examine whether the expression is a product, composition, or rational form.
If uncertainty remains, test strategies mentally. The method that reduces complexity rather than increasing it is typically the correct one.
Avoid defaulting to advanced techniques prematurely—most AP-level integrals break down with one well-chosen step.
Use geometric reasoning when:
• The function represents simple shapes such as lines, constant functions, or known curves forming recognisable areas.
• Computing the antiderivative is more complex than identifying the enclosed area visually.
Geometric insight is also helpful when symmetry exists, such as identical areas on either side of an axis.
This strategy often saves time and demonstrates a sophisticated understanding of the integral’s meaning, provided the region is straightforward to interpret.
Practice Questions
Question 1 (1–3 marks)
A student is asked to evaluate a definite integral of a function that is the product x ln(x). They immediately choose substitution with u = ln(x).
(a) Explain why substitution is not the most efficient method in this case.
(b) State the more appropriate integration method and justify the choice based on the structure of the integrand.
Question 1
(a)
• 1 mark for explaining that substitution with u = ln(x) does not simplify the integral meaningfully or leads to a more complicated integrand.
• 1 mark for noting that the structure (a product where one factor simplifies when differentiated) suggests an alternative method.
(b)
• 1 mark for identifying integration by parts as the more appropriate method.
• 1 mark for justifying that differentiating ln(x) simplifies it, while x is easy to integrate, making the method efficient.
Maximum: 3 marks.
Question 2 (4–6 marks)
A function is defined by
f(x) = (3x + 2) / (x + 1).
A student wants to evaluate the definite integral from x = 0 to x = 3.
(a) Describe the first strategic step that should be taken before attempting to integrate, and explain why this step is appropriate.
(b) Rewrite f(x) in a form suitable for integration using the strategy identified in part (a).
(c) State the integration method that should be applied once the expression is rewritten.
(d) Without performing the full integration, justify why this method is more effective than using substitution or integration by parts.
Question 2
(a)
• 1 mark for identifying that algebraic manipulation should be carried out first.
• 1 mark for explaining that the rational function should be rewritten using polynomial long division to simplify the integrand.
(b)
• 1 mark for correctly rewriting f(x) in the form 3 + (−1)/(x + 1) or an equivalent simplification.
• 1 mark for expressing the function clearly as a sum of simpler terms.
(c)
• 1 mark for stating that basic integration rules should be applied after rewriting (power rule and logarithmic integration).
(d)
• 1 mark for justifying that the rewritten form splits the integrand into easily integrable terms, avoiding unnecessary complexity.
• 1 mark for correctly explaining why substitution or integration by parts would be inefficient for a rational expression of this type.
Maximum: 6 marks.

