Indefinite integrals provide a powerful way to recover original functions from their rates of change, forming families of antiderivatives that differ only by constant vertical shifts.

Indefinite Integrals and Antiderivative Families

The study of indefinite integrals centers on understanding how integration reverses differentiation to produce a complete family of functions whose derivatives equal a given function. When we write an expression such as $\int f(x),dx$, we are not computing a numerical value; instead, we are identifying all functions whose derivatives return the integrand. This perspective is essential because AP Calculus AB students must interpret indefinite integrals as representing infinitely many related functions.

The term antiderivative appears throughout this subsubtopic, and it is crucial to recognize that indefinite integrals communicate far more than a single function. They express an entire collection of valid results tied together through the addition of a constant of integration.

Because indefinite integrals correspond to reverse differentiation, they play a foundational role in connecting the algebraic rules of differentiation to the broader structure of integration. To emphasize the generality of this relationship, we include the arbitrary constant C, ensuring that every member of the family is represented.

Notation and Structure of the Indefinite Integral

The notation $\int f(x),dx$ includes several meaningful components that students should understand clearly.

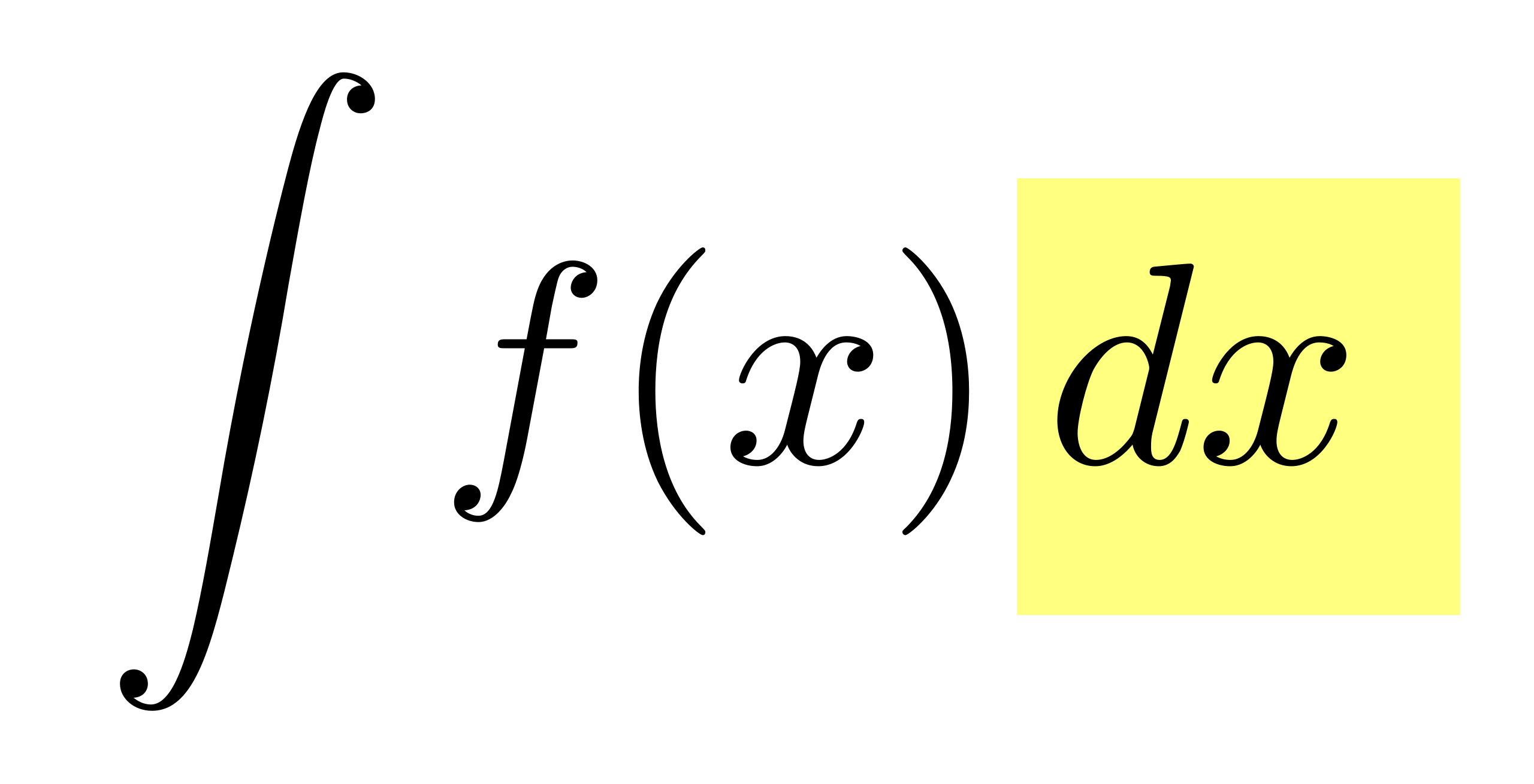
This diagram shows the expression $\int f(x),dx$ with the variable of integration emphasized. It distinguishes the integral sign, the integrand $f(x)$, and the differential $dx$, reinforcing how each part contributes to the meaning of an indefinite integral. The image includes only notation-level detail, consistent with the focus on interpreting $\int f(x),dx$ rather than evaluating it. Source.

The elongated integral sign suggests accumulation, the integrand $f(x)$ specifies the rate being reversed, and dx identifies the variable of integration. Together, these elements package the entire process of reversing the derivative into a single expression.

Indefinite integrals always require the explicit inclusion of C, the constant of integration. This constant acknowledges the vertical shift between any two antiderivatives of the same function. Without this term, the representation of the family would be incomplete. Because differentiation eliminates constant terms, integration must reintroduce this missing variable component.

A sentence must separate equation blocks and definition blocks, ensuring clarity as concepts develop throughout the notes.

Understanding the Constant of Integration

Every time an indefinite integral is computed, the result must include + C, which symbolizes the entire family of functions sharing the same derivative.

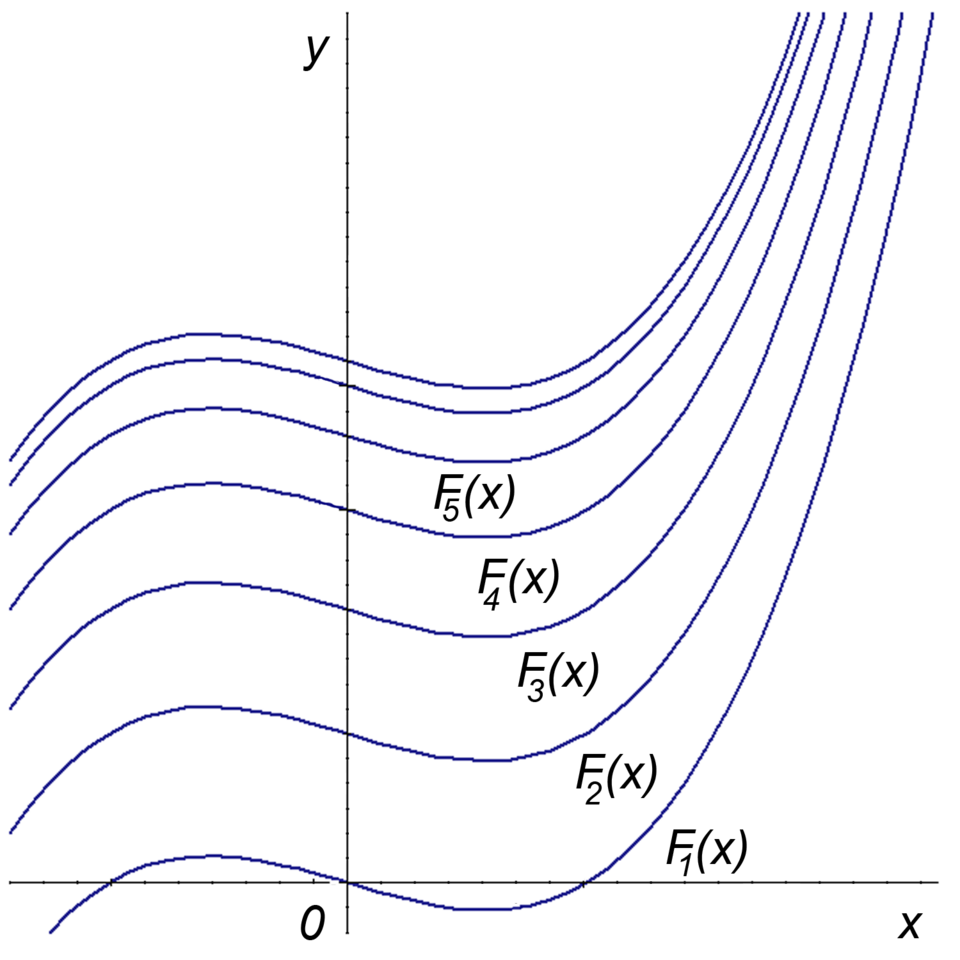
This graph shows multiple antiderivatives $F_i(x)$ of the same function $f(x)$, each curve shifted vertically by a different constant. It reinforces that $\int f(x),dx$ represents a family of functions defined by vertical translations corresponding to the constant of integration $C$. The specific choice $f(x)=3x^2 - 2$ appears in the source image but is not required by the syllabus. Source.

This constant is essential—omitting it results in only one member of the family, not the complete set. The constant represents all possible vertical translations of an antiderivative.

This constant becomes especially important in applied contexts where initial conditions or contextual constraints determine which specific antiderivative is appropriate. Although those applications are handled in later subsubtopics, the conceptual foundation established here is crucial.

Reversing Differentiation Through Indefinite Integration

Indefinite integration relies on reversing known differentiation rules. While detailed techniques are introduced in later sections of the syllabus, the essential idea is that indefinite integrals produce families of curves whose derivatives recreate the given rate. Students should recognize that the notation communicates a relationship rather than a numeric quantity. In contrast to definite integrals, indefinite integrals never yield accumulated amounts or areas.

The inclusion of dx is non-negotiable; it identifies which variable is being integrated, especially useful when expressions involve multiple variables or substitutions. By interpreting $\int f(x),dx$ as the complete family of antiderivatives, students build a solid framework for later techniques such as substitution, partial fractions, and integration by parts.

Key Properties of Indefinite Integrals

Indefinite integrals share structural properties that mirror derivative rules. Although this section does not list every formula, understanding the general behaviors of antiderivatives strengthens mathematical reasoning. Important characteristics include:

• Families of solutions: Every indefinite integral yields infinitely many functions due to the constant of integration.

• Variable dependence: The variable after the differential symbol determines the independent variable of the antiderivative.

• Reversibility: Differentiating an antiderivative always returns the original integrand.

• Symbolic interpretation: Indefinite integrals represent expressions, not numerical values.

• Linearity: The integral of a sum equals the sum of integrals, and constants may be factored out.

These properties allow students to connect symbolic manipulation with conceptual understanding. They also reinforce the idea that indefinite integration is inherently general, mapping each rate of change to a continuous family of possible original functions.

Interpreting the Indefinite Integral in AP Calculus AB

For AP purposes, the critical requirement is the ability to interpret the notation clearly and accurately. When reading $\int f(x),dx$, students should think “the family of all antiderivatives of $f(x)$.” This perspective aligns with the syllabus emphasis that indefinite integrals represent the entire family of antiderivatives plus the constant C. Understanding this concept prepares students for later topics, including solving differential equations and applying the Fundamental Theorem of Calculus.