AP Syllabus focus:
‘Students use values from a differential equation to sketch short line segments at selected points in the plane, creating a slope field that summarizes the local behavior of solution curves.’
Constructing slope fields by hand helps visualize how solutions to a differential equation behave locally, using short line segments that show slopes determined directly from the derivative expression.
Understanding Manual Construction of Slope Fields
A slope field is a graphical summary of a first-order differential equation. It displays information about how solution curves behave without requiring an explicit solution. Each point on the grid holds a small segment whose slope matches the value of the derivative at that point.

Slope field for the differential equation shown on a rectangular grid. Each short segment is centered at a grid point and has slope equal to the value of at that point. The figure reinforces how evaluating the derivative at each point produces a field of local tangent directions without yet drawing full solution curves. Source.
This visual structure emphasizes how a differential equation directs the shape of its solution family.
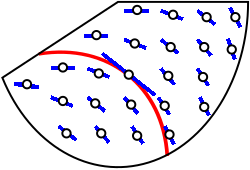
Slope field for a first-order differential equation, with one integral curve drawn through the field. The short line segments indicate the slope prescribed by the differential equation at each point, and the curve is always tangent to these segments. The presence of the integral curve goes slightly beyond this subsubtopic but clearly illustrates how solution graphs emerge from the slope field you construct. Source.
When we write a first-order differential equation of the form , it defines a slope for every point in the plane. The process of constructing a slope field by hand relies entirely on interpreting these slope values and representing them consistently across a selected grid.
Interpreting the Derivative in a Slope Field
The derivative expression gives the slope of a tangent line at each point. To construct the slope field correctly, the relationship between , , and must be read with precision. For example, if the derivative depends only on x, slopes change horizontally but stay constant vertically.
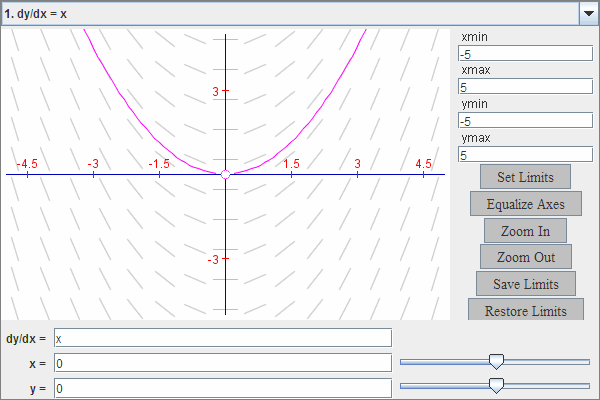
Static slope field for the differential equation , with one solution curve drawn in a contrasting color. The gray line segments form vertical columns of equal slope, reflecting that the derivative depends only on the -coordinate. The highlighted solution curve is an additional feature not required by this subsubtopic but helps students see how solutions follow the directions set by the slope field. Source.
If it depends only on y, slopes remain constant along horizontal lines. If the derivative involves both variables, slopes vary across both axes.
= Slope of the tangent line at point
= Rule assigning slope based on the values of and
Before placing slope segments, it is important to recognize whether the derivative simplifies or reveals patterns. This awareness supports more efficient sketching and more accurate interpretation of local behavior.
Preparing the Grid for Manual Sketching
Constructing a slope field requires selecting a finite grid of representative points. The grid must be coarse enough to complete manually, yet dense enough to reflect how slopes change across the plane. Students typically choose evenly spaced values for both axes. Since the goal is visual insight rather than computational precision, a moderate number of points is sufficient.
Choosing Points to Evaluate
The slope field emerges from evaluating the derivative at each selected point. Good practice involves:
Choosing a symmetric and manageable grid centered around the region of interest.
Ensuring that - and -values are simple enough for mentally computing slopes.
Labeling axes or keeping track of coordinate increments to avoid placing segments at incorrect points.
After choosing coordinates, each point becomes a location where the slope value will determine the direction of its corresponding segment.
Constructing Individual Line Segments
The heart of the subsubtopic is constructing each segment by hand using slope values from the differential equation. A slope segment is not a complete tangent line; rather, it is a short mark that visually conveys the local direction of a potential solution curve.
Steps for Drawing Each Segment
Evaluate the derivative at the chosen coordinate pair.
Interpret the numerical slope: Is it positive, negative, zero, or undefined?
Draw a short segment centered on the grid point, angled so its slope matches the computed value.
Maintain consistency in segment length so the field appears uniform and readable.
Because slope fields summarize behavior qualitatively, the goal is accuracy in slope direction, not in the length of segments. Uniformity helps the viewer follow solution patterns.
Recognizing Visual Patterns While Sketching
As the slope field takes shape, several patterns may emerge. Observing these patterns reinforces understanding of how the derivative influences solutions.
Common Structural Patterns
Zero slopes produce horizontal segments that may indicate equilibrium solutions or stable values.
Positive slopes reveal increasing trends, with steeper slopes reflecting faster growth.
Negative slopes signal decreasing behavior.
Undefined or nonreal slopes leave gaps or vertical tendencies, depending on whether the derivative expression is undefined or infinite at particular points.
These visual cues help reveal direction fields, regions of steep change, and potential boundaries in solution behavior.
Maintaining Accuracy While Sketching
Although slope fields are qualitative, precision still matters. Small inaccuracies can obscure important structural features. Attention must be given to:
Consistency in segment angle
Correct evaluation of slope signs and magnitudes
Proper placement of segments exactly at designated grid points
Recognizing repeating patterns that reflect the dependence on , , or both
These habits ensure that the slope field accurately communicates the information encoded by the differential equation.
Purpose and Interpretation of Hand-Drawn Slope Fields
Manually constructed slope fields help students understand how a differential equation conveys information about a function’s behavior. Because the sketch emerges point by point, the student sees directly how the derivative governs the shape of solution curves. This supports intuitive understanding of solution families and prepares students for later work with solution interpretation, qualitative analysis, and general solution behavior.
FAQ
Select a scale that balances clarity with efficiency. A grid that is too fine becomes time-consuming, while one that is too coarse hides important slope variation.
A good approach is:
• Use evenly spaced integers or simple fractions.
• Ensure the chosen region contains the behaviour you wish to illustrate.
• Keep axes proportional so slopes are visually accurate.
A consistent scale helps prevent exaggerating or flattening slopes, which could distort the qualitative behaviour of solution curves.
When the computed slope is large, the goal is not precision but representing the correct direction.
You may:
• Draw a segment angled steeply, even if the exact gradient is difficult to capture.
• Shorten the segment while preserving direction to avoid clutter.
• Indicate vertical tendencies carefully without letting lines overlap or appear like full tangent lines.
The emphasis is always on local direction, not exact steepness.
Yes. If the derivative expression is undefined at certain coordinates, do not draw a slope segment there.
This creates:
• A visible break or structural gap in the slope field.
• A cue that solution curves may not cross that region or may behave differently near it.
Leaving these points blank helps reflect the limitations of the differential equation and improves the accuracy of the qualitative picture.
Recognising symmetry can significantly reduce computation and sketching time.
For example:
• If the derivative depends only on the x-coordinate, slopes remain identical along vertical lines.
• If it depends only on the y-coordinate, slopes remain identical along horizontal lines.
• Evenness or oddness in the derivative formula can create mirrored behaviour across axes.
Using symmetry lets you fill multiple points quickly after calculating just a few slopes.
Use small visual tests to ensure consistency across the grid.
Useful checks include:
• Ensuring slopes that should match—by symmetry or repeated values—actually do match on your sketch.
• Verifying that slopes transition smoothly across the plane rather than changing abruptly unless the derivative dictates it.
• Looking for unintended patterns, such as overly horizontal or vertical segments that do not reflect the derivative.
A quick scan for uniform segment length and correct placement often catches errors before the field is finalised.
Practice Questions
Question 1 (1–3 marks)
A differential equation is given by dy/dx = 2x − y.
At the point (1, 3), determine the slope of the line segment that would appear in the hand-drawn slope field.
Explain what this slope indicates about the behaviour of a solution curve passing through that point.
Question 1
• 1 mark for substituting x = 1 and y = 3 correctly into dy/dx = 2x − y.
• 1 mark for obtaining the correct slope value: 2(1) − 3 = −1.
• 1 mark for a correct interpretation, such as stating that the solution curve through (1, 3) is decreasing at that point or would be drawn with a downward-sloping segment.
Total: 3 marks
Question 2 (4–6 marks)
Consider the differential equation dy/dx = y − x.
A student wishes to construct a slope field by hand on a grid containing the points (0, 0), (1, 1), (2, 1), and (2, 3).
(a) For each of these points, calculate the slope of the segment that should be drawn.
(b) Describe one clear pattern that would emerge in the slope field based on your calculated slopes.
(c) Explain how this slope field helps a student understand the qualitative behaviour of solution curves, even without solving the differential equation.
Question 2
(a) Slopes
• 1 mark for the slope at (0, 0): 0 − 0 = 0.
• 1 mark for the slope at (1, 1): 1 − 1 = 0.
• 1 mark for the slope at (2, 1): 1 − 2 = −1.
• 1 mark for the slope at (2, 3): 3 − 2 = 1.
(b) Pattern
• 1 mark for identifying a correct pattern, such as slopes increasing as y increases or slopes becoming more negative as x increases.
(c) Interpretation
• 1 mark for explaining that the slope field shows local behaviour and indicates the general shape of solution curves without solving the equation.
Total: 6 marks

